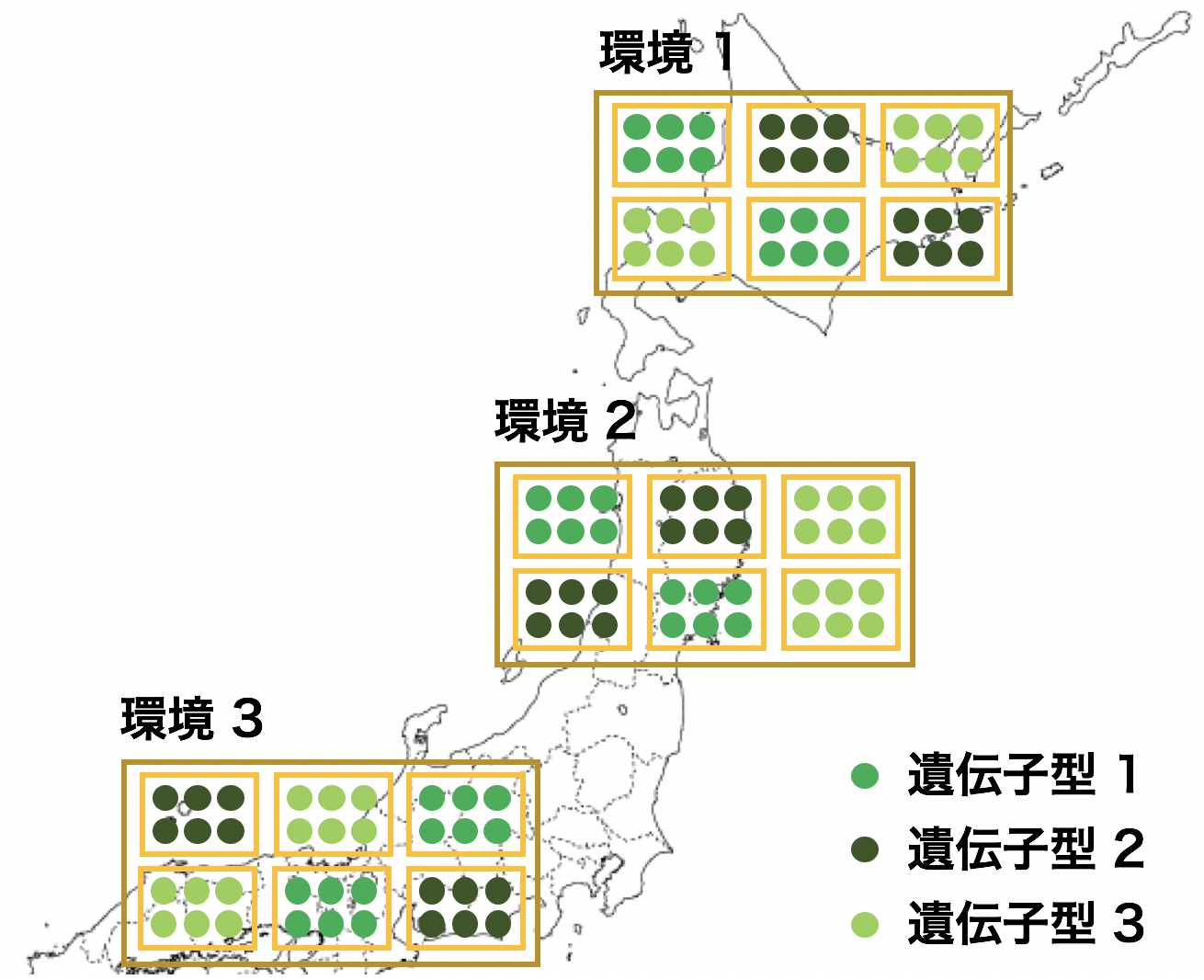
一般化線形モデルを利用した GxE 解析では、まず、表現型 P を応答変数(従属変数)とし、遺伝子型 G、環境 E および遺伝子型と環境の相乗効果 GE を説明変数(独立変数)としてモデルを構築している。続いて、このモデルに対して分散分析(ANOVA)を行い、遺伝子型と環境の相乗効果 GE の項の評価を行う。実際の GxE における多環境試験では、次のように、複数の遺伝子型の個体を使用して、複数の環境において複数個の区画で栽培実験が行われて、データが取られる。
| 環境 1 | 環境 2 | 環境 3 | |
| 遺伝子型 1 | 反復 1: 289 ton/ha 反復 2: 301 ton/ha | 反復 1: 202 ton/ha 反復 2: 215 ton/ha | 反復 1: 246 ton/ha 反復 2: 239 ton/ha |
| 遺伝子型 2 | 反復 1: 203 ton/ha 反復 2: 224 ton/ha | 反復 1: 221 ton/ha 反復 2: 208 ton/ha | 反復 1: 214 ton/ha 反復 2: 198 ton/ha |
| 遺伝子型 3 | 反復 1: 328 ton/ha 反復 2: 335 ton/ha | 反復 1: 269 ton/ha 反復 2: 245 ton/ha | 反復 1: 243 ton/ha 反復 2: 258 ton/ha |
このように集計されたデータに対して、環境 Ej における遺伝子型 Gi の条件で観測された反復区画 k における表現型 Pij (例えば、平均収量)とすると、次の式でモデル化できる。ただし、モデル式中の μ は、各効果の総平均を表し、εijk は、環境 Ej における遺伝子型 Gi の条件における反復区画 k のランダム誤差を表す。
\[ P_{ijk} = \mu + G_{i} + E_{j} + GE_{ij} + \epsilon_{ijk} \] \[ \epsilon \sim N(0, \sigma^{2}_{\epsilon_{ij}}) \]次に、モデル化したデータに対して二元配置の分散分析を行う。この二元配置の分散分析では、帰無仮説を「各因子(遺伝子型と環境)が変化しても、表現型の平均値は変化しない」こととしている。この二元配置の分散分析を通して、遺伝子型の違いがデータ全体(の表現型)の平均値に有意な差を与えたかどうか、環境の違いがデータ全体の平均値に有意な差を与えたかどうか、そして遺伝子型と環境の交互作用がデータ全体の平均値に有意な差を与えたかどうか、を検定することができる。
環境が複数想定されるとき、モデル式中の E を展開して対応する。例えば、環境 E は年度 Y と実験区域 L に分けられるとき、Yn 年度に実験区域 Lm で行われた実験データの場合は、次のようにしてモデル化できる。
\[ P_{ijmn} = \mu + G_{i} + L_{m} + Y_{n} + LY_{mn} + GL_{im} + GY_{jn} + GLY_{imn} + \epsilon_{ijmn} \] \[ \epsilon \sim N(0, \sigma^{2}_{\epsilon_{ijmn}}) \]遺伝子型と環境は必要に応じて増やすことができる。そのため、解析対象の因子が多くなると、モデルに含まれる変数の数も増えて、モデルが複雑になる。また、分散分析を行うためには、これらの変数間の等分散性を仮定する必要である。環境因子が異なれば、その等分散性は必ずしも保証されなくなる。そのため、分散分析の結果が正しくない危険性も生じてくる。これらの問題があることから、現在では、一般的に GxE 解析は混合モデルをベースとして行われている。