ベイジアンネットワークでは、確率変数間の因果関係をグラフで表すことができる。確率変数（あるいは事象）をグラフのノードで表し、各事象の因果関係や条件付き確率をグラフのエッジで表す。以下に、いくつかのシンプルなベイジアンネットワークとそのときの同時確率を示す。

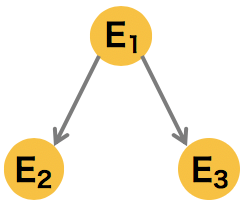
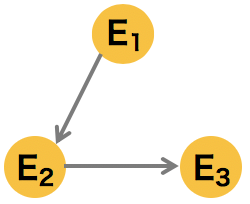
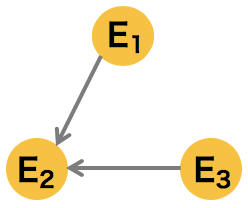
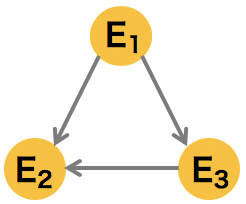
3 ノードで構成されるシンプルなグラフの例

\[ p(E_{1}, E_{2}, E_{3}) = p(E_{3}|E_{1})p(E_{2}|E_{1})p(E_{1})\]

\[ p(E_{1}, E_{2}, E_{3}) = p(E_{3}|E_{2})p(E_{2}|E_{1})p(E_{1})\]

\[ p(E_{1}, E_{2}, E_{3}) = p(E_{2}|E_{3})p(E_{3})p(E_{2}|E_{1})p(E_{1})\]

\[ p(E_{1}, E_{2}, E_{3}) = p(E_{2}|E_{3})p(E_{3}|E_{1})p(E_{2}|E_{1})p(E_{1})\]

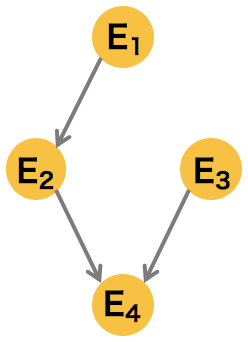
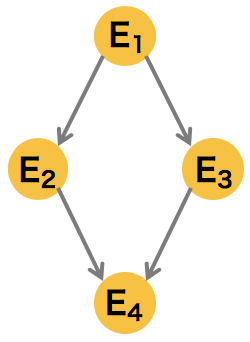
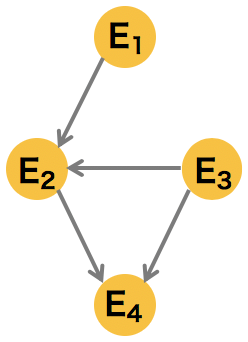
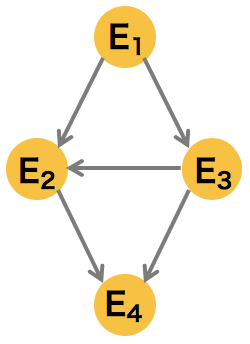
4 ノードで構成されるシンプルなグラフの例

\[ p(E_{1}, E_{2}, E_{3}, E_{4}) = p(E_{4}|E_{3})p(E_{3})p(E_{4}|E_{2})p(E_{2}|E_{1})p(E_{1})\]

\[ p(E_{1}, E_{2}, E_{3}, E_{4}) = p(E_{4}|E_{3})p(E_{3}|E_{1})p(E_{4}|E_{2})p(E_{2}|E_{1})p(E_{1})\]

\[ p(E_{1}, E_{2}, E_{3}, E_{4}) = p(E_{4}|E_{3})p(E_{2}|E_{3})p(E_{3})p(E_{4}|E_{2})p(E_{2}|E_{1})p(E_{1})\]

\[ p(E_{1}, E_{2}, E_{3}, E_{4}) = p(E_{4}|E_{3})p(E_{4}|E_{2})p(E_{2}|E_{3})p(E_{3}|E_{1})p(E_{2}|E_{1})p(E_{1})\]