グラフィカルモデルは、確率変数間の関係をグラフの形で表現したモデルである。確率変数間に因果関係が存在するときに、グラフは「原因」→「結果」のように方向性を持つ。有向グラフを利用して、確率変数間に因果関係をグラフィカルに表現したネットワークをベイジアンネットワークという。ベイジアンネットワークは複数の原因と結果で複雑に構成されているが、ある一つの原因あるいは結果(ノード)に着目したときは、そのノードが極めてシンプルであり、そこに至るまでの確率も極めて簡単に計算できる。
基本的なグラフ構造
head-to-tail
3 つのノードからなるグラフが次のように A → B → C のように並ぶとき、その同時確率は次のようにかける。
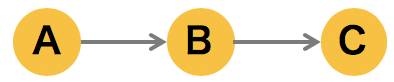
ここで、仮に事象 B の起こる確率が観測されたとき(B が条件づけられたとき)、このネットワークの同時確率分布は、乗法定理 p(A, C, B) = p(A, C| B)p(B) により次のように計算できる。
\[ p(A,C|B) = \frac{p(A, B, C)}{p(B)} = \frac{p(A)p(B|A)p(C|B)}{p(B)} = p(A|B)p(C|B) \]このようにグラフが head-to-tail の構造をとる場合は、B が条件づけられることによって、A と C が起こる確率は独立にになる。
tail-to-tails
3 つのノードからなるグラフが次のように A ← B → C のように並ぶとき、その同時確率は次のようにかける。
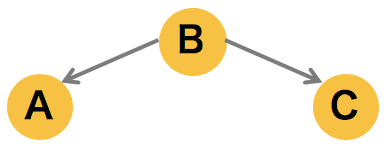
ここで、事象 B が条件づけられたとき、このネットワークの同時確率分布は、乗法定理 p(A, C, B) = p(A, C| B)p(B) により次のように計算できる。
\[ P(A,C|B) = \frac{p(A, B, C)}{p(B)} = \frac{p(A)p(B|A)p(C|B)}{p(B)} = p(A|B)p(C|B) \]このようにグラフが tail-to-tail の構造をとる場合も、B が条件づけられることによって、A と C が起こる確率は独立にになる。
head-to-head
3 つのノードからなるグラフが次のように A → B ← C のように並ぶとき、その同時確率は次のようにかける。
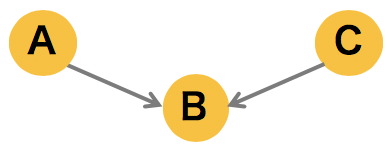
ここで、事象 B が条件づけられたとき、このネットワークの同時確率分布は、乗法定理 p(A, C, B) = p(A, C| B)p(B) により次のように計算できる。
\[ p(A, C|B) = \frac{P(A,B,C)}{p(B)} = \frac{p(A)p(C)p(B|A,C)}{p(B)} \ne p(A|B)p(C|B) \]このようにグラフが head-to-head の構造をとる場合は、B が条件づけられることによって、もともと互いに独立であった A と C が、互いに依存するようになる。例えば、事象 A および事象 C はそれぞれサイコロを降って出た目を確率変数として、事象 B を事象 A と事象 C の合計としたとき、A と C はもともと独立な事象であるが、B (= A + C)が観測されると、A と C は互いに影響を及ぼしあう状態となる。