同時確率
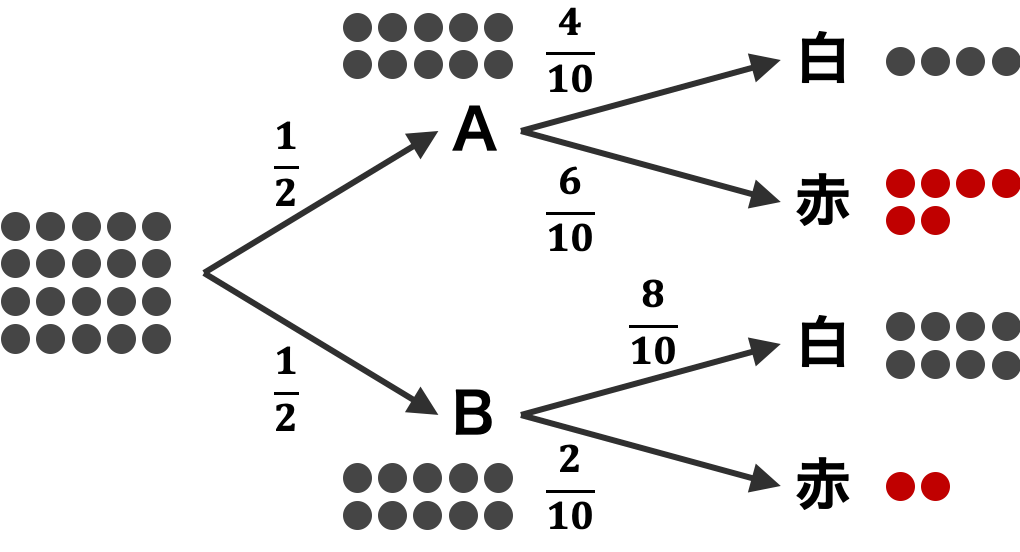
同時確率について考える。2 つの袋 A と B がある。袋 A の中には赤玉が 6 個、白玉が 4 個ある。袋 B の中には赤玉 8 個、白玉が 2 個ある。いま、袋 A および袋 B それぞれから玉を 1 つずつ同時に取り出す。このとき、両方とも赤玉である同時確率は、次のように計算できる。
袋 A と袋 B から玉を取り出す作業は、互いに独立である。そのため、袋 A および袋 B それぞれから玉を 1 つずつ同時に取り出す操作は、袋 A から玉を 1 つ取り出してから袋 B から玉を 1 つ取り出す操作と等しい。このとき、袋 A から取り出した玉が赤玉である条件下で、袋 B から取り出した玉も赤玉である確率は次のように求めることができる。
\[ \begin{eqnarray} && P(A = red)P(B=red | A=red) \\ &=& P(A = red)P(B = red) \\ &=& \frac{6}{10}\frac{2}{10} = \frac{12}{100} \end{eqnarray} \]同様に、袋 A および袋 B それぞれから玉を 1 つずつ同時に取り出す操作は、袋 B から玉を 1 つ取り出してから袋 A から玉を 1 つ取り出す操作とも等しい。このとき、袋 B から取り出した玉が赤玉である条件下で、袋 A から取り出した玉も赤玉である確率は次のように求めることができる。
\[ \begin{eqnarray} && P(B = red)P(A=red | B=red) \\ &=& P(B = red)P(A = red) \\ &=& \frac{2}{10}\frac{6}{10} = \frac{12}{100} \end{eqnarray} \]条件付き確率
2 つの袋から玉を取り出す操作について、袋 A から取り出してから袋 B から取り出す操作と、袋 B から取り出してから袋 A から取り出す操作は同等である。つまり、次の式が成り立つ。
\[ P(A = red)P(B=red | A=red) = P(B = red)P(A=red | B=red) \]袋 A から赤玉を取り出したという条件下で、袋 B から赤玉を取り出す確率は、次のように計算できる。この前提条件がついている確率のことを条件付き確率という。
\[ P(B=red | A=red) = \frac{P(B = red)P(A=red | B=red)}{P(A = red)} \]袋 A から赤玉を取り出したときの確率 P(A = red) は、「袋 B から白玉かつ袋 A から赤玉」と「袋 B から赤玉かつ袋 A から赤玉」を取り出したときの確率の和に等しい。すなわち、
\[ \begin{eqnarray} && P(B=red | A=red) \\ &=& \frac{P(B = red)P(A=red | B=red)}{P(B=red)P(A = red|B=red) + P(B=white)P(A=red|B=white)} \\ &=& \frac{P(B = red)P(A=red | B=red)}{\sum_{c = red, white} P(B=c)P(A=red|B=c) } \end{eqnarray} \]この式の中の A は袋 A の中から赤玉を取り出す操作、B は袋 B から赤玉を取り出す操作を表している。この操作を別の例で考えてみる。A をそのまま「袋 A の中から赤玉を取り出す操作」として、B を「袋 A を選ぶ操作」とする。すると、上の式は、ある袋を選んで、その袋から玉を 1 つ取り出して、それが赤玉だったとき、袋 A が選ばれる確率を表している。
\[ \begin{eqnarray} && P(B=bag A | A=red) \\ &=& \frac{P(B = bag A)P(A=red | B=bag A)}{\sum_{bag = A, B} P(B=bag)P(A=red|B=bag) } \end{eqnarray} \]この式を一般化してみる。袋が複数あり、その中から袋 i を選ぶ操作を Ei とおく。また、袋 i の中から赤玉を取り出す操作を F とおく。すると、上の式は、ある袋を選んで、その中から玉を取り出したとき、それが赤玉だったとき、選んだ袋が袋 i である確率を求める式となる。
\[ P(E_{i}|F) = \frac{P(E_{i}P(F|E_{i}))}{\sum_{i}P(E_{i})P(F|E_{i})} \]さらに一般化してみると、Ei を数多くある原因のうち i 番目の原因(袋 i が原因)とし、F を観測結果(赤玉だった)としたとき、この式は、F という結果が観測したとき、原因 Ei である確率を求める式となる。
図示による条件付き確率の求め方
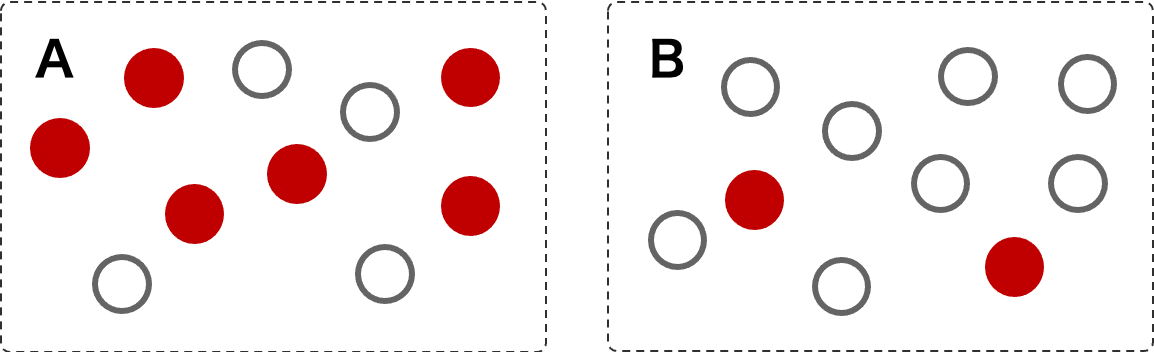
数式を利用せずに、簡単な条件付き確率であれば図から簡単に計算できる。2 つの袋 A と B がある。袋 A の中には赤玉が 6 個、白玉が 4 個ある。袋 B の中には赤玉 8 個、白玉が 2 個ある。いま、ある袋から玉を 1 つだけ取り出して、それが赤玉だった。このとき、その袋が A である確率について考える。ただし、袋 A と袋 B が選ばれる確率は等しい。
まず、スタートから袋を選ぶ確率、そして各袋から白玉および赤玉を取り出す確率の道のりを描く。このとき、ある袋から玉を取り出して、その玉が赤玉であれば、必ず path1 または path2 を通ることになる。この 2 つのパスのうち、path1 を通る確率を計算できれば、ある袋から玉を 1 つだけ取り出して、それが赤玉であったとき、その袋が A である確率が求まる。
\[ \frac{path1}{path1+path2} = \frac{\frac{1}{2}\frac{6}{10}}{\frac{1}{2}\frac{6}{10} + \frac{1}{2}\frac{2}{10}} = \frac{6}{8} \]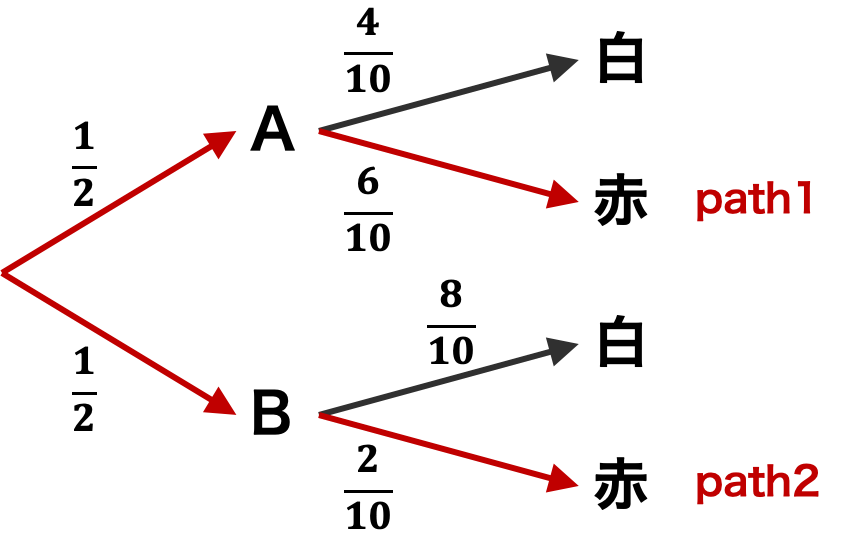
また、次のように考えることもできる。20 個の玉を用意して、下図のようなパスに転がす。すると、玉はパス上に書かれている確率に従って分配されて、最後に辿り着く。このとき、A を経由して赤にたどり着いた玉は 6 個であり、B を経由して赤にたどり着いた玉は 2 である。このとき、ある袋から玉を 1 つだけ取り出して、それが赤玉であったとき、その袋が A である確率は次のように計算できる。
\[ \frac{6}{6+2} = \frac{6}{8} \]