二項分布は、確率 p で成功する試行を N 回独立に試行を行った時の成功回数 x が従う確率分布である。Stan では binomial 関数を使ってモデルを構築することができる。ここで、R を使用して二項分布に従う乱数を 100 個生成して、次に Stan で乱数が生成された二項分布のパラメーターを推定する例を示す。

x <- rbinom(n = 100, size = 20, prob = 0.8)

Stan を利用して x を生成した二項分布のパラメーター p を求める。Stan コードの data ブロックには、これから入力する値である成功回数 x と試行回数 N を定義する。次に、parameters ブロックには、これから推定したい二項分布のパラメーターである確率 p を定義する。パラメーター p は確率であるから、その範囲は 0≤p≤1 であることがわかっているので、そのように定義する。最後に、model ブロックで、入力値変数とパラメーター変数を使って二項分布モデルを構築する。

data {
    int N;
    int n;
    int x[n];
}
parameters {
    real<lower=0, upper=1> p;
}
model {
    x ~ binomial(N, p);
}

R では、次のようにして Stan コードを呼び出して実行する。推定結果を見ると、確率 p は 0.81 に推定され、乱数生成するときに設定した確率 0.8 に近いことがわかる。

d <- list(N = 20, x = x, n = length(x))
fit <- stan(file = 'binomialdisp.stan', data = d)
fit
## Inference for Stan model: tmp.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##         mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
## p       0.81    0.00 0.01    0.79    0.8    0.81    0.81    0.82  1473    1
## lp__ -987.71    0.02 0.68 -989.64 -987.9 -987.45 -987.27 -987.22  1603    1

各回 MCMC サンプリングの結果をプロットする場合は、stan_trace 関数を利用し、パラメーターの事後確率のヒストグラムをプロットする場合は stan_hist 関数を利用する。

stan_trace(fit)
stan_hist(fit)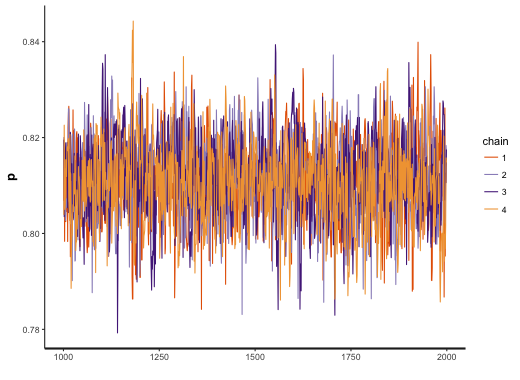

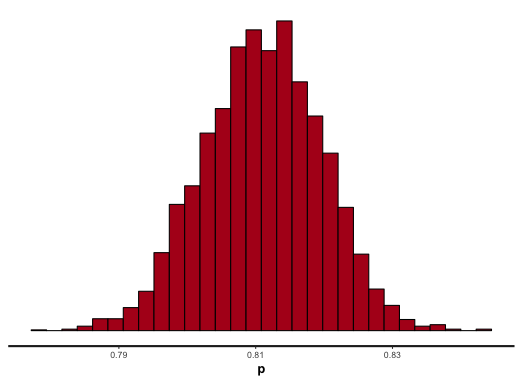
MCMC サンプリング結果は、そのままパラメーターが取りうる値とみなすことができる。そのため、α/2 分位点から 1 - α/2 分位点までの区間は、そのパラメーターにおける (1 - α)% のベイズ信用区間とみなすことができる。このことを利用して、平均と標準偏差の 95% 信用区間を求めるには、次のように計算すればいい。

ms <- rstan::extract(fit)
quantile(ms$p, probs = c(0.025, 0.975))
##      2.5%     97.5%
## 0.7879047 0.8222818