カテゴリカル分布は順序情報のないカテゴリデータを扱うための文法である。例えば、地域名、種名、性別などがカテゴリデータにあたる。サイコロの振り目も 1 から 6 までの数字として出るが、これらの数値には（解析目的によっては）順序情報が含まれていないと考えることができる。例えば、賞金設定で 2 がでたら 500 円、 3 がでたら 900 円のように、必ずしも目が大きいと意味があるわけではない。

ここでサイコロの振り目データを乱数で発生させて、各目がどれぐらいの確率で出るのかを Stan で推定してみる。まず、少し不公平なサイコロの振り目データを 100 個作成する。このとき、1, 2, 3, 4, 5, 6 が出る確率をそれぞれ 0.3, 0.1, 0.1, 0.2, 0.2, 0.1 とする。

x <- sample(1:6, 100, replace = TRUE, prob = c(0.3, 0.1, 0.1, 0.2, 0.2, 0.1))
table(x)
##  1  2  3  4  5  6
## 28 11  8 25 19  9

次に、Stan コードを利用してモデルを記述していく。サイコロの各目の出る確率を求めたいので、その確率をベクトル θ とおく。このときベクトル θ は 6 個の要素を持ち、それらの合計値が 1.0 となる。Stan では、ベクトルの合計値が 1.0 となるように制限が存在するとき、vector 型の代わりに simplex 型を用いると便利である。

data {
    int N;
    int M;
    int y[N];
}
parameters {
    simplex[M] theta;
}
model {
    for (n in 1:N) {
        y[n] ~ categorical(theta);
    }
}

続いて R で Stan コードを読み込んで、データを代入してパラメーターを推定していく。

d <- list(y = x, N = length(x), M = length(unique(x)))
fit <- stan(file = 'multi_norm.stan', data = d)
fit
## Inference for Stan model: multi_norm.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##             mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
## theta[1]    0.27    0.00 0.04    0.19    0.24    0.27    0.30    0.36  4761    1
## theta[2]    0.11    0.00 0.03    0.06    0.09    0.11    0.13    0.18  4334    1
## theta[3]    0.08    0.00 0.03    0.04    0.06    0.08    0.10    0.14  4422    1
## theta[4]    0.25    0.00 0.04    0.17    0.22    0.24    0.27    0.33  4130    1
## theta[5]    0.19    0.00 0.04    0.12    0.16    0.19    0.21    0.27  4983    1
## theta[6]    0.09    0.00 0.03    0.05    0.07    0.09    0.11    0.16  5203    1
## lp__     -181.98    0.04 1.61 -186.02 -182.78 -181.64 -180.80 -179.88  1843    1

推定されたパラメーターの情報は上のように fit 変数を表示させれば、画面上に表示される。95% 信用区間を自分で求めたい場合は、次のようにする。

ms <- rstan::extract(fit)
apply(ms$theta, 2, quantile, probs = c(0.025,  0.975))
##              [,1]       [,2]       [,3]      [,4]      [,5]       [,6]
##   2.5%  0.1931747 0.06016473 0.04020945 0.1694428 0.1207068 0.04658794
##   97.5% 0.3630181 0.18112827 0.14349897 0.3314907 0.2707293 0.15697648

サイコロの振り目 1, 2, 3, 4, 5, 6 が出る確率をそれぞれ 0.3, 0.1, 0.1, 0.2, 0.2, 0.1 としてデータを生成したので、この真の値と推定された 95% 信用区間を見比べると、真の値がすべて 95% 信用区間に含まれていることがわかる。

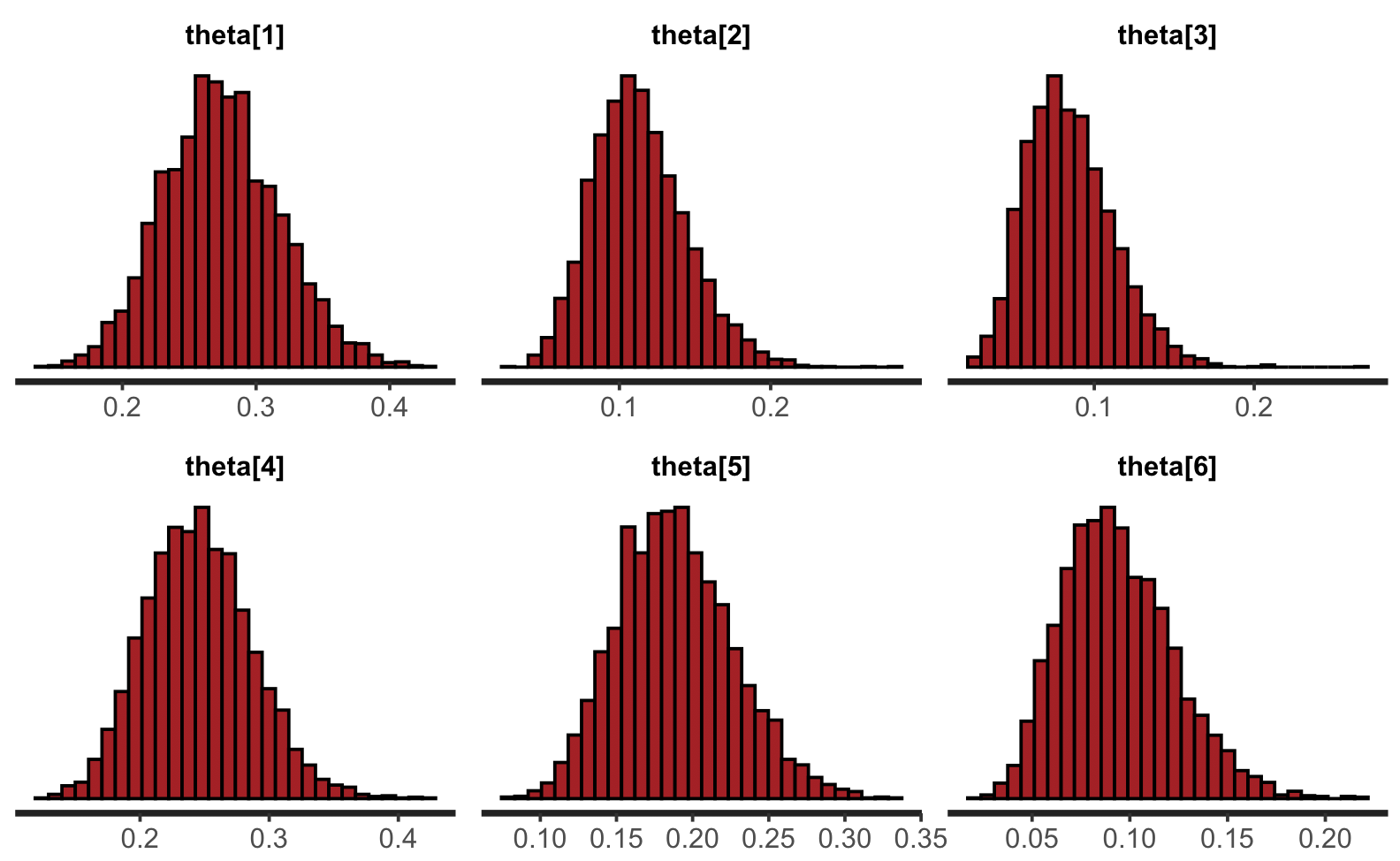
各パラメーターの分布図は stan_hist 関数で描くことができる。

stan_hist(fit)