多変量正規分布 | R / Stan による多変量正規分布の平均と分散共分散行列の推定

多変量正規分布のパラメーターには平均ベクトル μ と分散共分散行列 Σ がある。例えば、2 変量正規分布の場合は、2 つの変量（X1 と X2）それぞれの平均 μ_X1 と μ_X2 が存在し、それぞれの分散 σ_X1 と σ_X1 が存在する。これらに加えて、変数 X1 と X2 の共分散も存在する。

\[ \begin{pmatrix} X_{1} \\ X_{2} \end{pmatrix} \sim MultiNorm \left( \boldsymbol{\mu}, \boldsymbol{\Sigma} \right)\] \[ \boldsymbol{\mu} = \begin{pmatrix} \mu_{X_{1}} \\ \mu_{X_{2}} \end{pmatrix} \] \[ \boldsymbol{\Sigma} = \begin{pmatrix} \sigma_{X_{1}} & \sigma_{X_{1}X_{2}} \\ \sigma_{X_{2}X_{1}} & \sigma_{X_{2}} \end{pmatrix} \]

ここでは、乱数を使って 2 変量正規分布に従うサンプルデータを生成して、R/Stan を利用してその 2 変量正規分布のパラメーターを推定する例を示す。2 変量正規分布を生成するとき、2 つの変数の平均をそれぞれ 10 および 20 とし、標準偏差をそれぞれ 2.0 および 1.0 とする。また、2 変数間の共分散を 0.5 とする。

mu <- c(10, 20)
cov <- matrix(c(2.0, 0.5, 0.5, 1.0), ncol = 2)
data <- mvrnorm(100, mu = mu, Sigma = cov)
colnames(data) <- c('X1', 'X2')

g <- ggplot(as.data.frame(data), aes(x = X1, y = X2))
g <- g + geom_point()
print(g)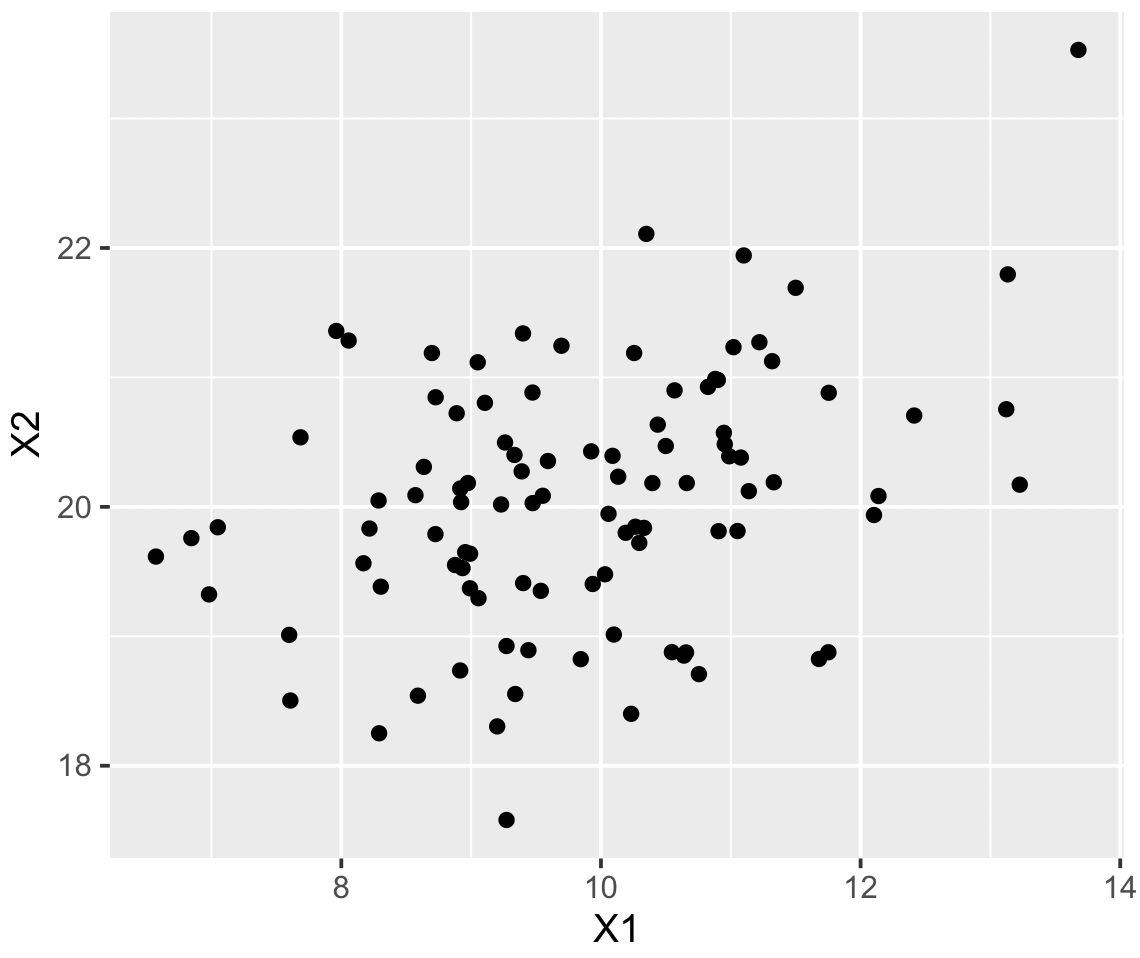

次に、Stan コードでモデルを記述していく。2 変量データを 1 セットと考えて Y = (X1, X2) とおける。サンプルデータは全部で 100 セットあるので、Y は 100 行 2 列の行列となる。Stan の data ブロックにおいて、入力データを N 行 M 列となるように定義する。また、parameters ブロックでは平均と分散を定義する。とくに分散については、分散共分散行列を cov_matrix 型で定義できる。

data {
    int N;
    int M;
    matrix[N, M]  y;
}
parameters {
    vector[M] mu;
    cov_matrix[M] cov;
}
model {
    for (n in 1:N) {
        y[n, ] ~ multi_normal(mu, cov);
    }
}

続いて、R で Stan コードを読み込み、データを代入し、パラメーター推定を行う。

d <- list(y = data, N = nrow(data), M = ncol(data))
fit <- stan(file = 'multi_norm.stan', data = d)
fit
## Inference for Stan model: multi_norm.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##             mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
## mu[1]      10.24    0.00 0.18    9.90   10.12   10.24   10.36   10.60  3914    1
## mu[2]      19.93    0.00 0.10   19.73   19.86   19.93   20.00   20.12  4376    1
## cov[1,1]    3.07    0.01 0.44    2.33    2.77    3.02    3.34    4.05  3911    1
## cov[1,2]    0.79    0.00 0.20    0.45    0.66    0.78    0.91    1.22  3485    1
## cov[2,1]    0.79    0.00 0.20    0.45    0.66    0.78    0.91    1.22  3485    1
## cov[2,2]    1.01    0.00 0.14    0.77    0.91    1.00    1.10    1.33  3361    1
## lp__     -138.01    0.03 1.54 -141.83 -138.81 -137.71 -136.87 -135.94  1936    1

パラメーターの推定結果を確認すると、2 変量の平均がそれぞれ 10.24 および 19.93 と推定された。これらはデータを生成するときに使用した 10 および 20 に非常に近い値となっていることがわかる。また、2 変量の分散を確認すると、それぞれが 3.07 および 1.01 となっている。データを生成するときに使用した 2.0 および 1.0 とは少しかけ離れていることがわかる。2 変量の共分散について 0.79 と推定され、データ生成に使った 0.5 と少し離れていることがわかる。95% 信用区間は上の結果で示されているが、個別に求めたい場合は、次のようにする。

ms <- rstan::extract(fit)
apply(ms$mu, 2, quantile, probs = c(0.025, 0.975))
##              [,1]     [,2]
##   2.5%   9.903138 19.72949
##   97.5% 10.595137 20.11932

apply(ms$cov[, 1, ], 2, quantile, probs = c(0.025, 0.975))
##           [,1]      [,2]
## 2.5%  2.329652 0.4452138
## 97.5% 4.052928 1.2195805

apply(ms$cov[, 2, ], 2, quantile, probs = c(0.025, 0.975))
##            [,1]      [,2]
## 2.5%  0.4452138 0.7671461
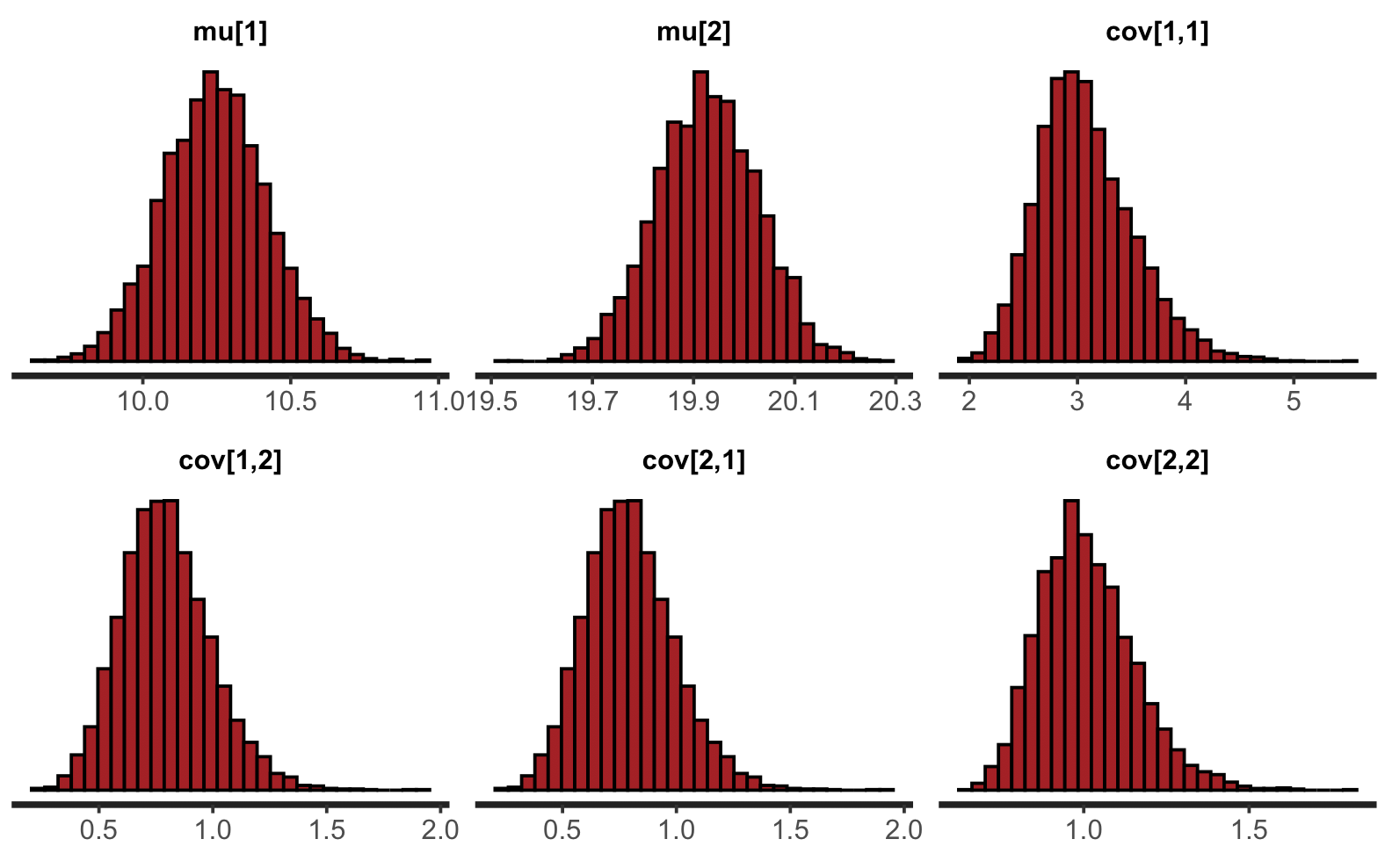
## 97.5% 1.2195805 1.3316161

各パラメーターの分布図は stan_hist 関数で描くことができる。

stan_hist(fit)