Stan を使うことで、時系列データの変化点を検出することができる。R に組み込まれた時系列データセットの中に、ナイル川の流量データ(Nile)というものがあり、1898 年と 1899 年の間に急に変化したことが知られている。このページではナイル川の流量データを利用して、変化点を検出する方法を示す。
data(Nile)
plot(Nile)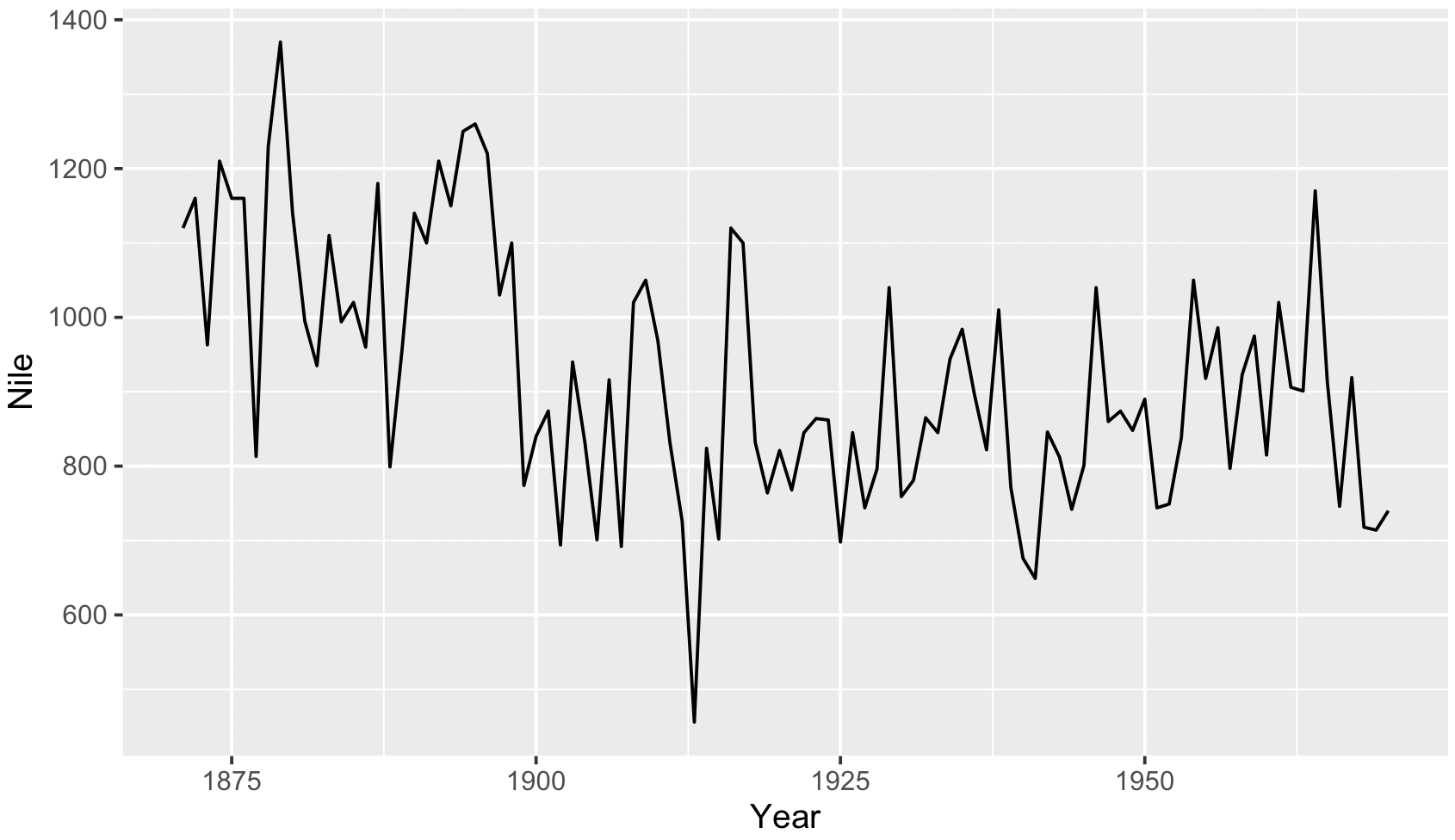
コーシー分布は左右対称な分布であり、正規分布に比べて尖度が大きい。正規分布の代わりに、コーシー分布を用いてモデルを構築したとき、平均値からかけ離れたデータが、モデルのパラメーター推定に与える影響が小さくなる。推定されたパラメーターの分布(信頼区間)の幅も小さくなる。そのため、推定後の時刻 t と時刻 t + 1 の分布の幅の重なりを見比べることで、変換点を検出しやすくなる。
ここで、Stan コードを用いて、状態空間モデルにおける状態方程式の平均を、コーシー分布からサンプリングするようにモデルを記述する。
data {
int N;
vector[N] Y;
}
parameters {
real mu0;
vector[N] mu;
real<lower=0> sigma_obs;
real<lower=0> sigma_sys;
}
model {
// state equation
mu[1] ~ normal(mu0, sigma_sys);
for(n in 2:N) {
mu[n] ~ cauchy(mu[n - 1], sigma_sys);
}
// observation equation
for(n in 1:N) {
Y[n] ~ normal(mu[n], sigma_obs);
}
}Stan コードを読み込み、ナイル川流量データを代入してパラメーター推定を行う。しかし、このコードを利用してパラメーター推定を行うと、エラーが生じ、状態方程式の平均のサンプリング回数を重ねることで、値をサンプリングできなくなる。
library(rstan)
data(Nile)
d <- list(Y = as.numeric(Nile), N = length(Nile))
fit <- stan(file = "ts.stan", data = d)
## Error in new_CppObject_xp(fields$.module, fields$.pointer, ...) :
## Exception: variable does not exist; processing stage=data initialization; variable name=Y; base type=double (in 'model111777e376a19_ts0' at line 3)
## failed to create the sampler; sampling not doneそこで、パラメーター変換を行い、Stan コードを修正して、もう一度パラメーター推定を行ってみる。
data {
int N;
real Y[N];
}
parameters {
real mu0;
vector<lower=-pi()/2, upper=pi()/2>[N-1] mu_pix;
real<lower=0> sigma_sys;
real<lower=0> sigma_obs;
}
transformed parameters {
vector[N] mu;
mu[1] = mu0;
for (n in 2:N) {
mu[n] = mu[n - 1] + sigma_sys * tan(mu_pix[n - 1]);
}
}
model {
Y ~ normal(mu, sigma_obs);
}d <- list(Y = as.numeric(Nile), N = length(Nile))
fit <- stan(file = "ts.stan", data = d)次に、推定された状態空間モデルの状態の平均値および 95% 信頼区間を図示する。図示された結果を見ると、ナイル川の流量は 1898 年と 1899 年の間に急に変化したことがわかる。
ms <- rstan::extract(fit, pars ='mu')
library(ggplot2)
df.conf <- data.frame(x = time(Nile),
y = as.numeric(Nile),
lower = apply(ms$mu, 2, quantile, prob = 0.025),
median = apply(ms$mu, 2, quantile, prob = 0.500),
upper = apply(ms$mu, 2, quantile, prob = 0.925))
g <- ggplot(df.conf, aes(x = x, y = y))
g <- g + geom_ribbon(aes(ymin = lower, ymax = upper), fill = '#000000', alpha = 0.4)
g <- g + geom_line(aes(y = median), color = '#CC0C00')
g <- g + geom_line(data = data.frame(x = time(Nile), y = as.numeric(Nile)), aes(x = x, y = y))
g <- g + xlab('Year') + ylab('Nile')
print(g)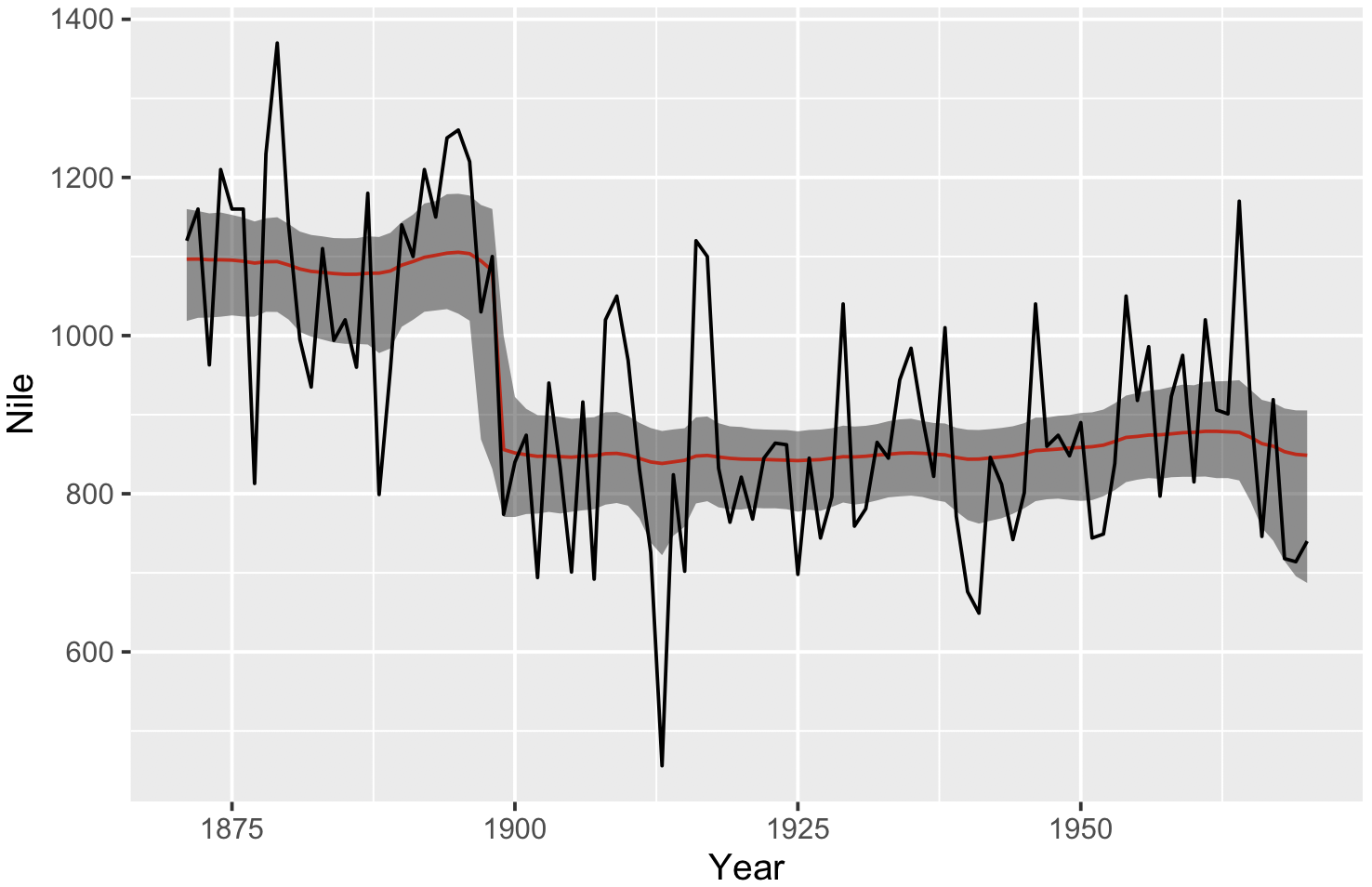
References
- Stan と R でベイズ統計モデリング. 共立出版