階層モデル（単回帰） | Stan で階層ベイズモデルの構築およびパラメーターの推測

このページでは、Stan を使って個体差を考慮した単回帰モデルを構築する方法を示す。サンプルデータとして R に標準実装されている Orange とよばれるデータセットを使用する。このデータセットは、個体番号（Tree）、樹齢（age）、周長（circumference）の 3 列からなる。ここで、樹齢を使って周長を説明するモデルを構築することを目的とする。

data(Orange)
head(Orange)
##   Tree  age circumference
## 1    1  118            30
## 2    1  484            58
## 3    1  664            87
## 4    1 1004           115
## 5    1 1231           120
## 6    1 1372           142

plot(Orange$age, Orange$circumference, col = Orange$Tree)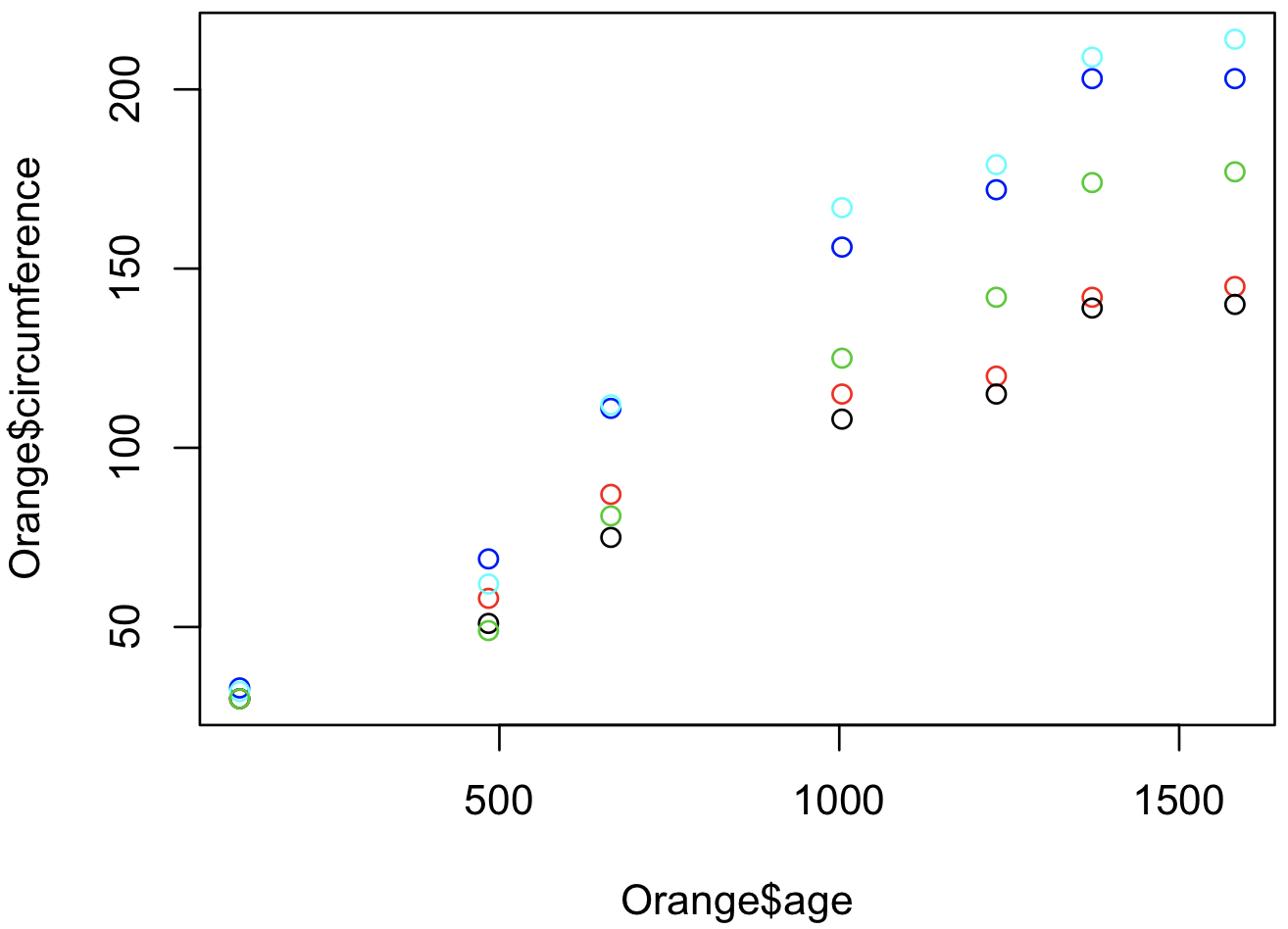

Stan モデル

Stan でモデルを記述していく。Orange データセットには 5 つの個体のデータが入っている。個体差を考慮に入れたモデルを構築したいので、まず個体差を表すパラメーターを導入する。全個体の（線型予測子の）平均を beta_ave とおいたとき、個体 1〜5 の個体差は平均からどれぐらい離れているかで表すことができる。その差をパラメーターとして定義する。parameters ブロックでこれらのパラメーターを定義する。また、周長 y をサンプリングするために、平均だけでは不十分であるので、分散も必要である。そのため、パラメーターとして分散も parameters ブロックに加える。

平均と分散が用意できので、個体 i の周長 y は次にようにサンプリングすることができる。

\[ y \sim Normal\left( \mu_{i}, \sigma \right) \]

個体 i の平均は、個体差を考慮するので、次のように計算される。

\[ \beta_{0}^{(i)} = \beta_{0}^{overall} + \beta_{0}^{i\_diff\_from\_all} \] \[ \beta_{1}^{(i)} = \beta_{1}^{overall} + \beta_{1}^{i\_diff\_from\_all} \] \[ \mu_{i} = \beta_{0}^{(i)} + \beta_{1}^{(i)}x \]

このように、正規分布で使用する μ_i は、parameters ブロックで定義した β などではない。そのため、transformed parameters ブロックで、β などのパラメーターを平均 μ に変換する命令を記述する。

また、パラメーターを推定した後に、各個体について樹齢が 0〜1600 までの予測区間を計算したいので、generated quantities で推定されたパラメーターを使って再サンプリングを行なうように記述する。

data {
    // data points
    int N;
    real x[N];
    real y[N];

    // number of trees and tree ID information
    int T;
    int tree[N];

    // tree ages for prediction
    int new_N;
    real new_x[new_N];
}
parameters {
    // parameters for calculating the overall average
    real beta0_ave;
    real beta1_ave;

    // differences from the overall averages for each tree
    real beta0_diff[T];
    real beta1_diff[T];

    // standard deviation for sampling `y`
    real<lower=0> sigma;
}
transformed parameters {
    real beta0[T];
    real beta1[T];
    real mu[N];

    for (t in 1:T) {
        beta0[t] = beta0_ave + beta0_diff[t];
        beta1[t] = beta1_ave + beta1_diff[t];
    }

    for (n in 1:N) {
        mu[n] = beta0[tree[n]] + beta1[tree[n]] * x[n];
    }
}
model {
    for (n in 1:N) {
        y[n] ~ normal(mu[n], sigma);
    }
}
generated quantities {
    real muhat[new_N, T];
    real yhat[new_N, T];

    for (t in 1:T) {
        for (n in 1:new_N) {
            muhat[n, t] = beta0[t] + beta1[t] * new_x[n];
            yhat[n, t] =  normal_rng(muhat[n, t], sigma);
        }
    }
}

パラメーター推定

次に R の rstan パッケージを利用して、パラメーター推定を行う。

library(rstan)

new.x <- seq(0, 1600, 10)

x <- Orange$age
y <- Orange$circumference
treeid <- as.integer(Orange$Tree)

d <- list(x = x, y = y, N = length(x), tree = treeid, T = length(unique(treeid)),
          new_x = new.x, new_N = length(new.x))

fit <- stan(file = 'lm.stan', data = d)

上のコードを実行すると、実行結果が fit オブジェクトに保存される。このオブジェクトには様々な情報が含まれ、そのまま表示すると非常に見づらい。ここでは、5 つの木それぞれのパラメーター β₀ および β₁ の 95% 信頼区間を見てみる。

ms <- rstan::extract(fit, pars = c('beta0', 'beta1'))

apply(ms$beta0, 2, quantile, probs = c(0.025, 0.500, 0.975))
##              [,1]      [,2]      [,3]      [,4]     [,5]
##   2.5%   2.316493  6.720595 -9.149217  2.716527 -4.20210
##   50%   19.610563 24.550709  8.398044 19.193066 15.75030
##   97.5% 36.404058 40.306671 24.462012 34.905749 32.02995

apply(ms$beta1, 2, quantile, probs = c(0.025, 0.500, 0.975))
##               [,1]       [,2]       [,3]      [,4]      [,5]
##   2.5%  0.06455640 0.06534071 0.09601257 0.1099995 0.1183769
##   50%   0.08088153 0.08150999 0.11128441 0.1256886 0.1343835
##   97.5% 0.09763204 0.09872538 0.12810771 0.1421530 0.1525764

stan_hist(fit, pars = c('beta0', 'beta1'))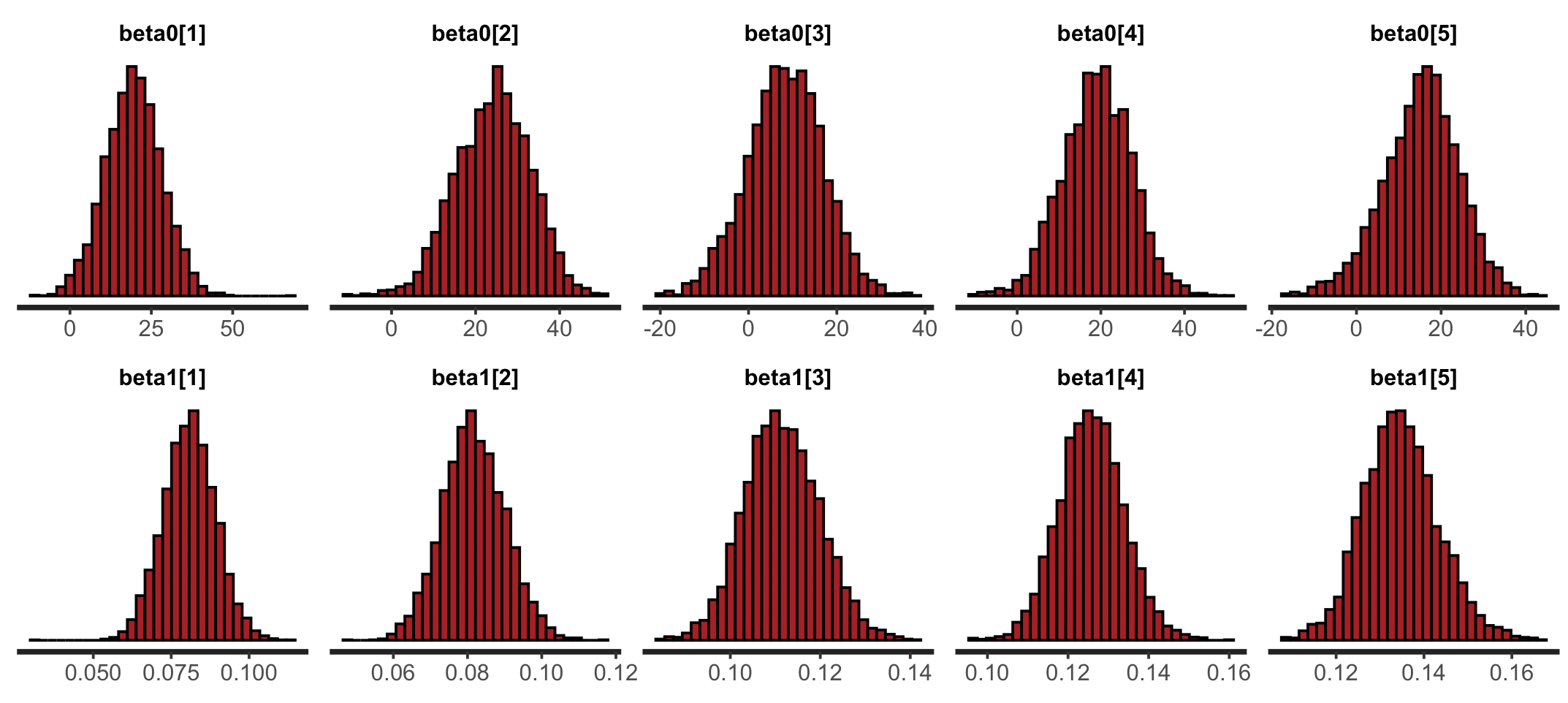

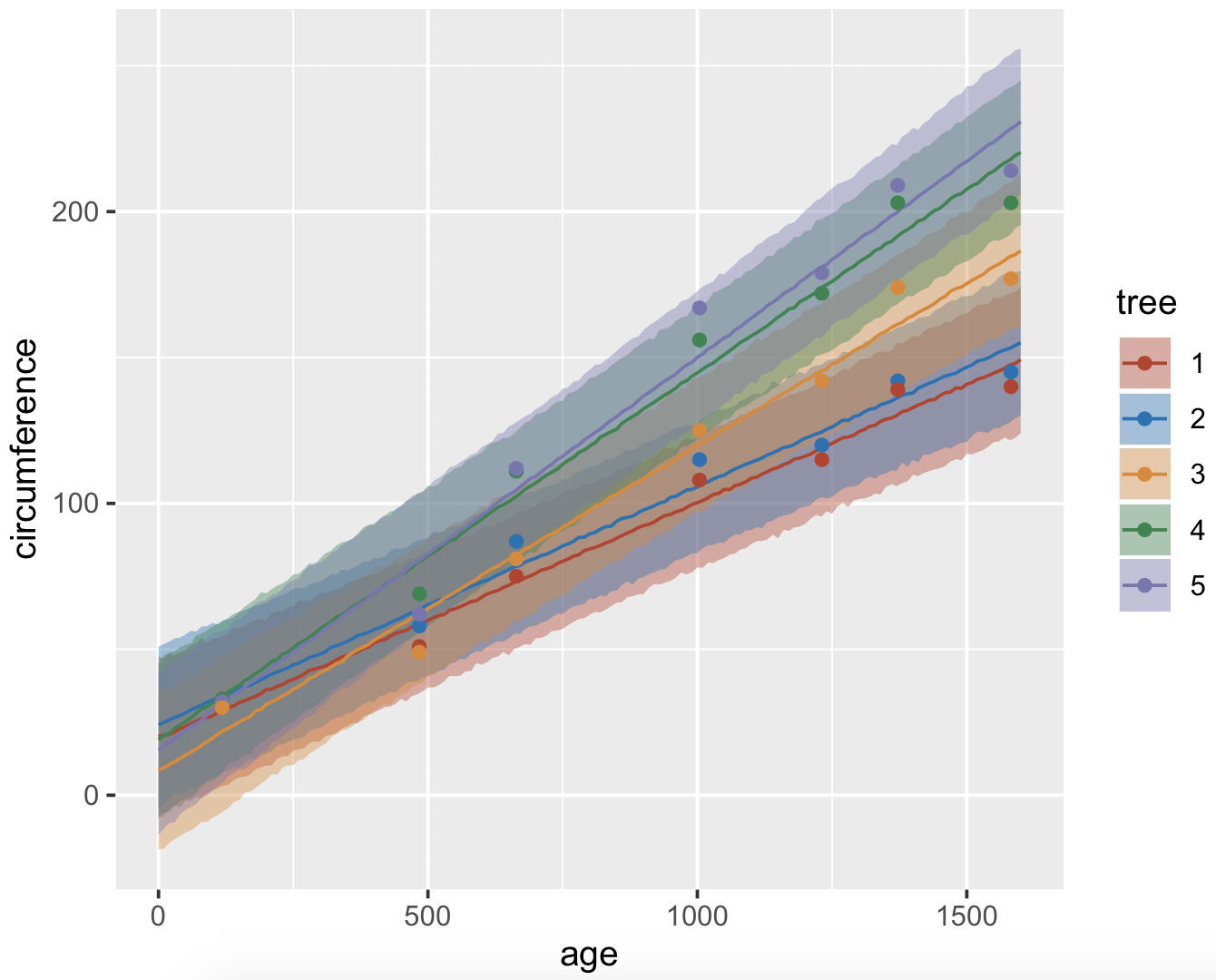
次に Stan コードの generated quantities のブロックで再サンプリングしたデータを用いて、個体ごとの予測区間を描く。

ms <- rstan::extract(fit, pars = c('yhat'))
dim(ms$yhat)

df <- NULL
for (i in 1:5) {
    df <- rbind(df,
                data.frame(x = new.x, tree = i,
                           lower = apply(ms$yhat[, , i], 2, quantile, prob = 0.025),
                           median = apply(ms$yhat[, , i], 2, quantile, prob = 0.500),
                           upper = apply(ms$yhat[, , i], 2, quantile, prob = 0.975)))

}
df$tree <- as.factor(df$tree)

library(ggplot2)
library(ggsci)
g <- ggplot(df, aes(x = x))
g <- g + geom_ribbon(aes(ymin = lower, ymax = upper, fill = tree), alpha = 0.4)
g <- g + geom_line(aes(y = median, color = tree))
g <- g + geom_point(data = data.frame(x = d$x, y = d$y, tree = as.factor(treeid)),
                    aes(x = x, y = y, colour = tree))
g <- g + scale_color_nejm() + scale_fill_nejm()
g <- g + xlab('age') + ylab('circumference')
print(g)