単回帰モデル | Stan を利用して回帰モデルのパラメーターを推定する方法

このページでは、Stan を使用して簡単な回帰モデルのパラメーターを推定する例を示す。ここで、サンプルデータとして、trees と呼ばれているデータセットを使用する。このデータセットには 31 本の桜の木の周長（Grith）、高さ（Height）、および容積（Volume）のデータが記録されている。樹木が高くなるには、それを支えるために幹も太くなる必要がある。そのため、幹が太さを用いて、木の高さを推定できるかもしれない。そこで、この仮定をもとに、Grith を説明変数とし、Height を応答変数として、回帰モデルを構築する。

data(trees)
head(trees)
##   Girth Height Volume
## 1   8.3     70   10.3
## 2   8.6     65   10.3
## 3   8.8     63   10.2
## 4  10.5     72   16.4
## 5  10.7     81   18.8
## 6  10.8     83   19.7

library(ggplot2)
g <- ggplot(trees, aes(x = Girth, y = Height)) + geom_point()
print(g)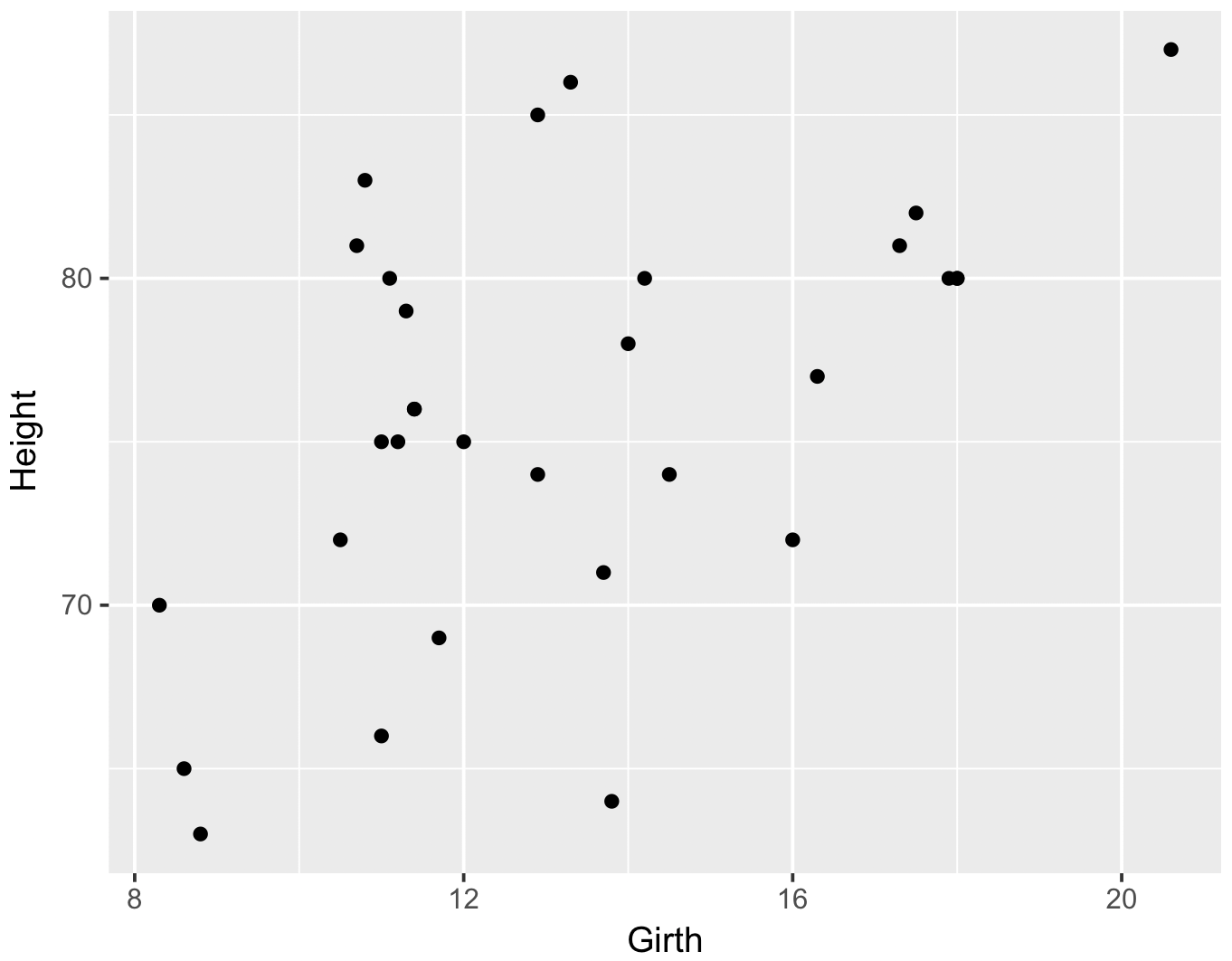

Stan コードによるモデル記述

単回帰モデルは、応答変数 y を説明変数 x で説明するモデルである。y と x の関係は次の関係がたり立つ。

\[ y = \mathcal{N}\left(\mu, \sigma \right)\] \[ \mu = \beta_{1}x + \beta_{0} \]

このモデルの入力データは x (Girth) と y (Height) であり、パラメーターは β₀、β₁ および σ である。x および y は、後から与える入力データであるので data ブロックで定義する。β₀、β₁ および σ は、これから MCMC サンプリングを通して推定したいパラメーターであるので、parameters ブロックで定義する。また、回帰モデルにおける信頼区間および予測区間を計算するために、推定されたパラメーター（β₀、β₁ および σ）を用いて、Girth が 5-30 の範囲にあるときの木の高さをサンプリングするコードを generated quantities ブロックに記述する。

// lm.stan
data {
  int N;
  vector[N] x;
  vector[N] y;

  int new_N;
  vector[new_N] new_x;
}
parameters {
  real beta_0;
  real beta_1;
  real<lower=0> sigma;
}
transformed parameters {
  real mu[N];
  for (i in 1:N) {
    mu[i] = beta_1 * x[i] + beta_0;
  }
}
model {
  for (i in 1:N) {
    y[i] ~ normal(mu[i], sigma);
  }
}
generated quantities {
  real yhat[new_N];
  real muhat[new_N];
  for (i in 1:new_N) {
    muhat[i] = beta_1 * new_x[i] + beta_0;
    yhat[i] = normal_rng(muhat[i], sigma);
  }
}

パラメーター推定

R からデータを Stan モデルに代入するとき、R でデータをリストとして用意する必要がある。Stan コードで記述された data ブロックには、x、y、N、new_x、new_N の変数が定義されている。R で準備するリストにもこれらの名前をつける必要がある。データを準備できたら、これを stan 関数に代入してパラメーター推定を行う。stan 関数が実行されると、MCMC サンプリング結果が返される。この結果に、parameters および generated quantities ブロックで定義されているパラメーターはの事後分布が含まれる。

library(rstan)
d <- list(x = trees$Girth, y = trees$Height, N = nrow(trees),
          new_x = seq(5, 30, 0.1), new_N = length(seq(5, 30, 0.1)))

fit <- stan(file = 'lm.stan', data = d)
fit
## Inference for Stan model: lm.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##             mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
## beta_0     62.07    0.12 4.54  52.83  59.10  62.14  65.01  71.07  1516    1
## beta_1      1.05    0.01 0.33   0.39   0.84   1.04   1.27   1.71  1511    1
## sigma       5.79    0.02 0.81   4.46   5.20   5.70   6.28   7.56  1643    1
## yhat[1]    67.19    0.12 6.59  53.71  62.94  67.26  71.54  80.32  3177    1
## yhat[2]    67.54    0.12 6.56  54.67  63.20  67.52  71.82  80.49  3224    1
## yhat[3]    67.65    0.12 6.54  54.79  63.25  67.64  71.90  80.39  3186    1
## ...
## yhat[248]  93.30    0.17 7.96  77.51  88.01  93.41  98.63 108.75  2304    1
## yhat[249]  93.32    0.16 8.10  76.58  87.98  93.61  98.73 108.88  2465    1
## yhat[250]  93.70    0.16 7.98  78.19  88.33  93.88  99.15 108.94  2537    1
## yhat[251]  93.74    0.16 8.16  77.65  88.26  93.76  99.21 109.42  2561    1
## ...
## muhat[1]    67.11    0.09 3.16  60.95  65.08  67.07  69.14  73.27  1125   1
## muhat[2]    67.22    0.09 3.13  61.12  65.21  67.18  69.22  73.33  1127   1
## muhat[3]    67.33    0.09 3.09  61.30  65.34  67.29  69.31  73.37  1129   1
## muhat[4]    67.44    0.09 3.06  61.46  65.47  67.41  69.40  73.40  1131   1
## ...
## muhat[249]  93.81    0.18 5.98  82.25  89.97  93.88  97.70 105.39  1078   1
## muhat[250]  93.92    0.18 6.02  82.28  90.05  93.98  97.84 105.56  1078   1
## muhat[251]  94.03    0.18 6.05  82.31  90.12  94.08  97.96 105.74  1078   1
## lp__       -67.48    0.05 1.38 -70.85 -68.11 -67.10 -66.50 -65.96   851   1

fit 変数にはパラメーター推定時の設定条件およびパラメーターの推定結果が記録されている。例えば、この場合、4 つの chain で、それぞれ 2000 回のサンプリングが行われたことがわかる。また、2000 回のサンプリングのうち、最初の 1000 回はウォーミングアップのステップで、パラメーター推定時に使われていない。また、thin は間引きの間隔を表し、thin=1 の場合は、間引きが行われていなく、サンプリング結果をすべてを用いてパラメーター推定が行われる。例えば、thin=2 の場合、サンプリング結果のうちパラメーター推定に使用するのは 1 個おきとなる。

推定されたパラメーターの要約統計量は結果の中間部分に表示される。上の例では、beta_0、beta_1、sigma が推定されたパラメーターの要約統計量である。また、muhat および yhat は、generated quantities ブロックで再サンプリングされた値の要約統計量である。これらのサンプリング結果は extract 関数を使用して、行列または配列の形で取得できる。

ベイズ信用区間

信用区間とは、あるパラメーター（例えば母平均）の事後分布において、真の値が 1-α % の確率で含まれる区間である。Stan でモデルを構築したときに generated quantities ブロックで母平均 muhat の事後分布をサンプリングしたので、このパラメーターを取得すれば、95% 信用区間を求めることができるようになる。

library(dplyr)
library(ggplot2)
ms <- rstan::extract(fit)

df <- data.frame(d$new_x, t(apply(ms$muhat, 2, quantile, probs = c(0.025, 0.500, 0.975))))
colnames(df) <- c('x', 'lower', 'median', 'upper')

g <- ggplot(df, aes(x = x))
g <- g + geom_ribbon(aes(ymin = lower, ymax = upper), fill = '#000000', alpha = 0.4)
g <- g + geom_line(aes(y = median))
g <- g + geom_point(data = trees, aes(x = Girth, y = Height))
g <- g + xlab('Girth') + ylab('Height')
print(g)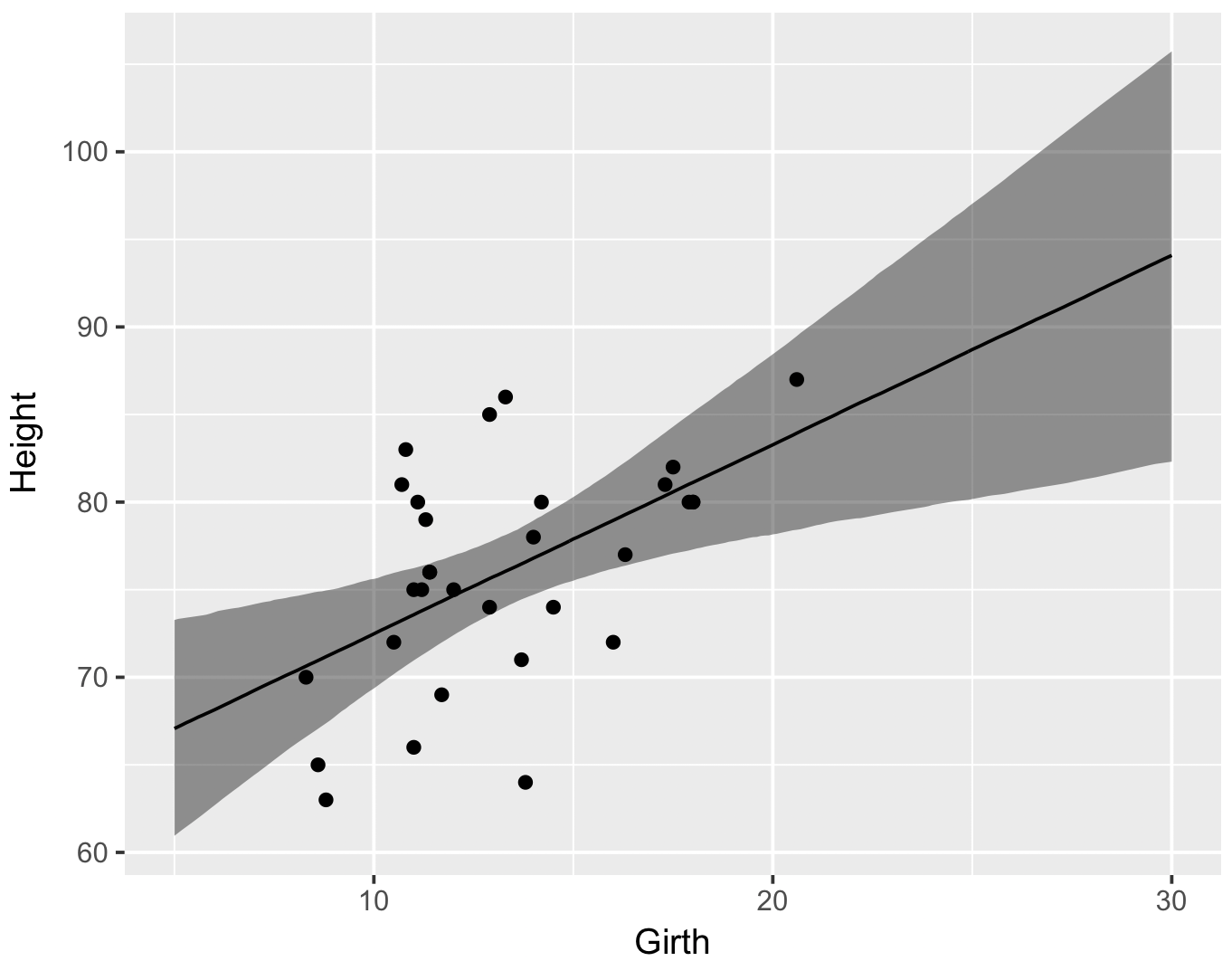

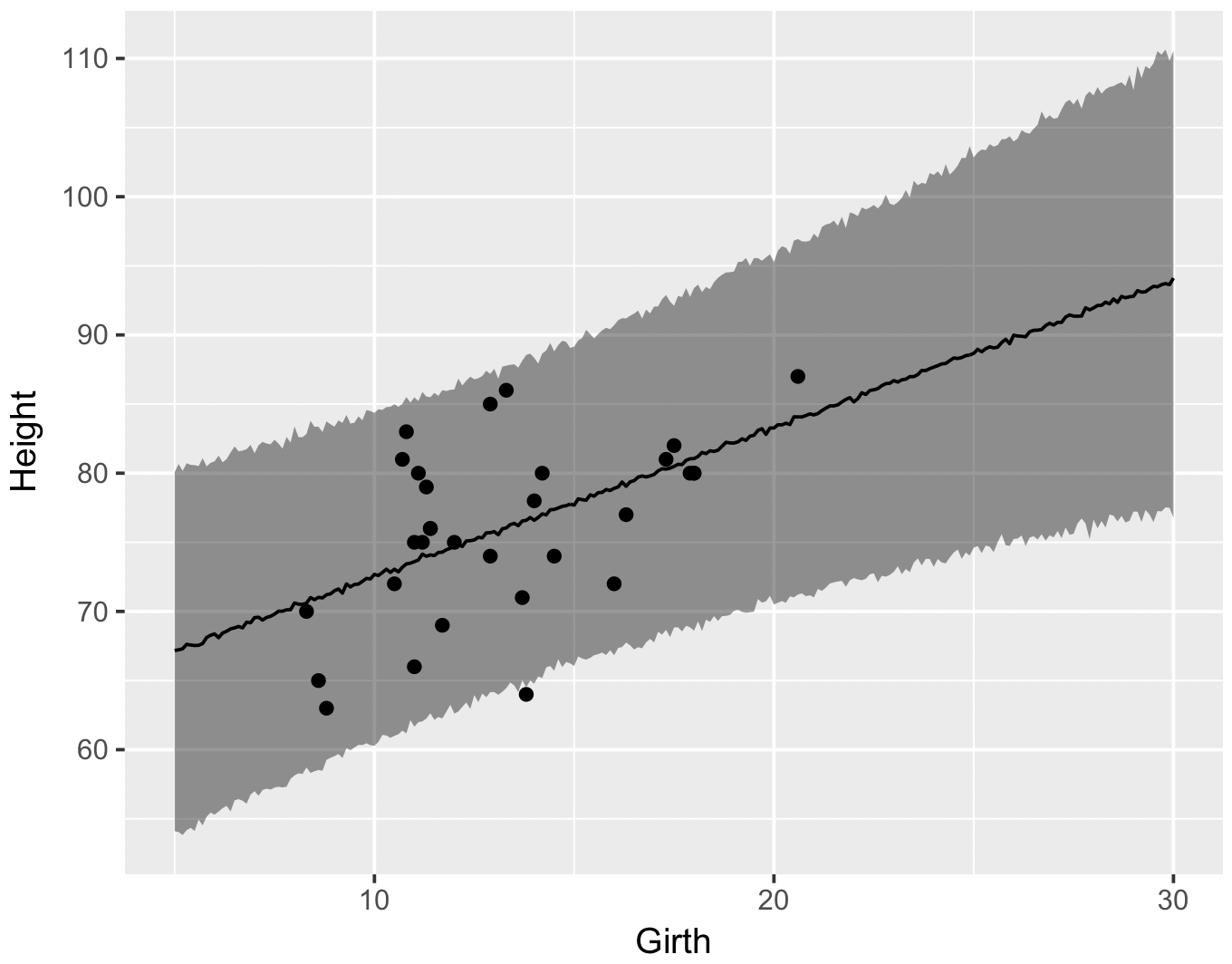
ベイズ予測区間

generated quantities ブロックでは、5-30 までの Girth を与えて、Height をサンプリングするように記述した。このサンプリング結果が yhat に保存される。ここで、extract 関数を用いて yhat のデータを取り出して、95% 予測区間を求める。

df <- data.frame(d$new_x, t(apply(ms$yhat, 2, quantile, probs = c(0.025, 0.500, 0.975))))
colnames(df) <- c('x', 'lower', 'median', 'upper')

g <- ggplot(df, aes(x = x))
g <- g + geom_ribbon(aes(ymin = lower, ymax = upper), fill = '#000000', alpha = 0.4)
g <- g + geom_line(aes(y = median))
g <- g + geom_point(data = trees, aes(x = Girth, y = Height))
g <- g + xlab('Girth') + ylab('Height')
print(g)