ロジスティック回帰は、特徴の有無、実験動物の生死などのような 2 つの値しか取り得ない 2 値データを解析する際に適用される。このページでは、悪性黒色腫(メラノーマ)のデータセットを使用して、生存時間と悪性黒色腫に起因した生死を、ロジスティック回帰を利用してモデル化する例を示す。
悪性黒色腫データ melanoma は、R の boot パッケージからを取得できる。この melanoma データには、悪性黒色腫を手術で取り除いた後の生存時間(月数)time、生存状態 status などの情報が記録されている。生存状態には 1, 2, 3 の整数が記録されている。1 は悪性黒色腫ににより死亡したことを表し、2 は調査打ち切りまで生存していたことを表し、3 は悪性黒色腫以外の原因で死亡したことを表す。ここで、モデルを構築するために、生存している場合に 1 を、悪性黒色腫により死亡した場合を 0 と表わすような変数 y を新たに作る。そして、この生存か死亡かを表わす変数 y を生存時間 x で説明する線型回帰モデルを構築する。なお、悪性黒色腫以外の原因で死亡したデータ(status が 3 のデータ)を取り除く。
※ロジスティック回帰を含む回帰モデルは、原因を用いて結果を説明するためのモデルである。このページでは、ロジスティック回帰モデルを構築するためのきれいなデータを見つけられませんでしたので、ロジスティック回帰できそうなこのデータで代用した。このデータの生存時間と悪性黒色腫の間に因果関係がなくて、本来は、このような解析を行なうべきではない。
data(melanoma, package = 'boot')
head(melanoma)
## time status sex age year thickness ulcer
## 1 10 3 1 76 1972 6.76 1
## 2 30 3 1 56 1968 0.65 0
## 3 35 2 1 41 1977 1.34 0
## 4 99 3 0 71 1968 2.90 0
## 5 185 1 1 52 1965 12.08 1
## 6 204 1 1 28 1971 4.84 1
x <- melanoma$time[melanoma$status != 3]
y <- ifelse(melanoma$status[melanoma$status != 3] == 2, 1, 0)
plot(x, y, xlab = 'time', ylab = 'alive')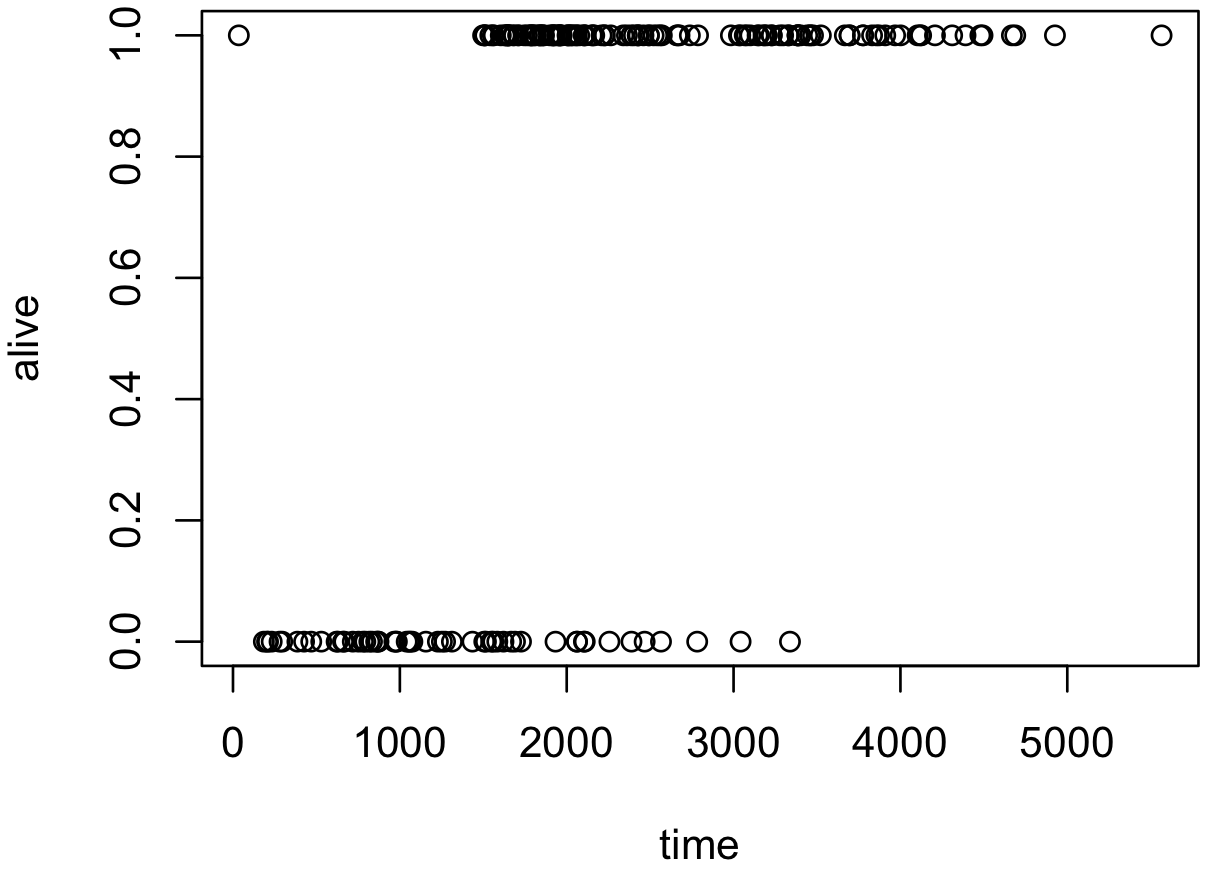
データを用意したら、次に Stan を利用を利用してモデルを記述していく。Stan コードでは、data ブロックには、観測データを入力するための変数である生存時間 x および生存状態 y を定義する。生存状態 y は、ベルヌーイ分布からサンプリングすることになる。このベルヌーイ分布から生存状態をサンプリングするには、パラメーターである死亡率が p を知る必要がある。
y をサンプリングできるようにするためには p を計算する必要がある。そこで、ロジスティック回帰で使われるリンク関数に着目して、変数変換を行う。
このとき、確率 p は次のように計算できる。
\[ p_{i} = logit^{-1}(\beta_{0} + \beta_{1}x) \]このような変数変換の作業を Stan コードの transformed parameters ブロックに記述する。
また、あとで予測区間も図示したいので、ここで generated quantities ブロックで推定されたパラメーターを使って再サンプリングを行うようにする。
data {
int N;
real x[N];
int y[N];
int new_N;
real new_x[new_N];
}
parameters {
real beta_0;
real beta_1;
}
transformed parameters {
real p[N];
for (n in 1:N) {
p[n] = inv_logit(beta_0 + beta_1 * x[n]);
}
}
model {
y ~ bernoulli(p);
}
generated quantities {
real phat[new_N];
real yhat[new_N];
for (n in 1:new_N) {
phat[n] = inv_logit(beta_0 + beta_1 * new_x[n]);
yhat[n] = bernoulli_rng(phat[n]);
}
}R でStan コードを呼び出して、ベイズ推定を行う。ただし、生存時間は数十から数千までの間の値を取り、スケールが非常に大きく、そのままパラメーター推定を行うと、不安定である。そこで、この生存時間を 1000 で割って、スケールを小さくしてからパラメーター推定を行うことにする。
library(rstan)
new.x <- seq(0, 6000, 1)
d <- list(x = x, y = y, N = length(x), new_x = new.x, new_N = length(new.x))
fit <- stan(file = 'logit.stan', data = d)
fit
## Inference for Stan model: logit.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
## beta_0 -3.49 0.02 0.70 -4.89 -3.96 -3.48 -3.01 -2.18 899 1
## beta_1 2.36 0.01 0.39 1.63 2.09 2.35 2.62 3.13 920 1
## p[1] 0.04 0.00 0.03 0.01 0.02 0.03 0.05 0.11 795 1
## p[2] 0.05 0.00 0.03 0.01 0.03 0.05 0.07 0.13 810 1
## p[3] 0.05 0.00 0.03 0.01 0.03 0.05 0.07 0.14 813 1
## ...
## yhat[598] 1.00 NaN 0.00 1.00 1.00 1.00 1.00 1.00 NaN NaN
## yhat[599] 1.00 NaN 0.00 1.00 1.00 1.00 1.00 1.00 NaN NaN
## yhat[600] 1.00 NaN 0.02 1.00 1.00 1.00 1.00 1.00 NaN 1
## lp__ -74.01 0.03 1.05 -76.82 -74.43 -73.69 -73.28 -73.00 1338 1
ms <- rstan::extract(fit, pars = 'phat')
dim(ms$phat)
## [1] 4000 600
df.pred <- data.frame(x = x, lower = apply(ms$phat, 2, quantile, prob = 0.025),
median = apply(ms$phat, 2, quantile, prob = 0.500),
upper = apply(ms$phat, 2, quantile, prob = 0.925))
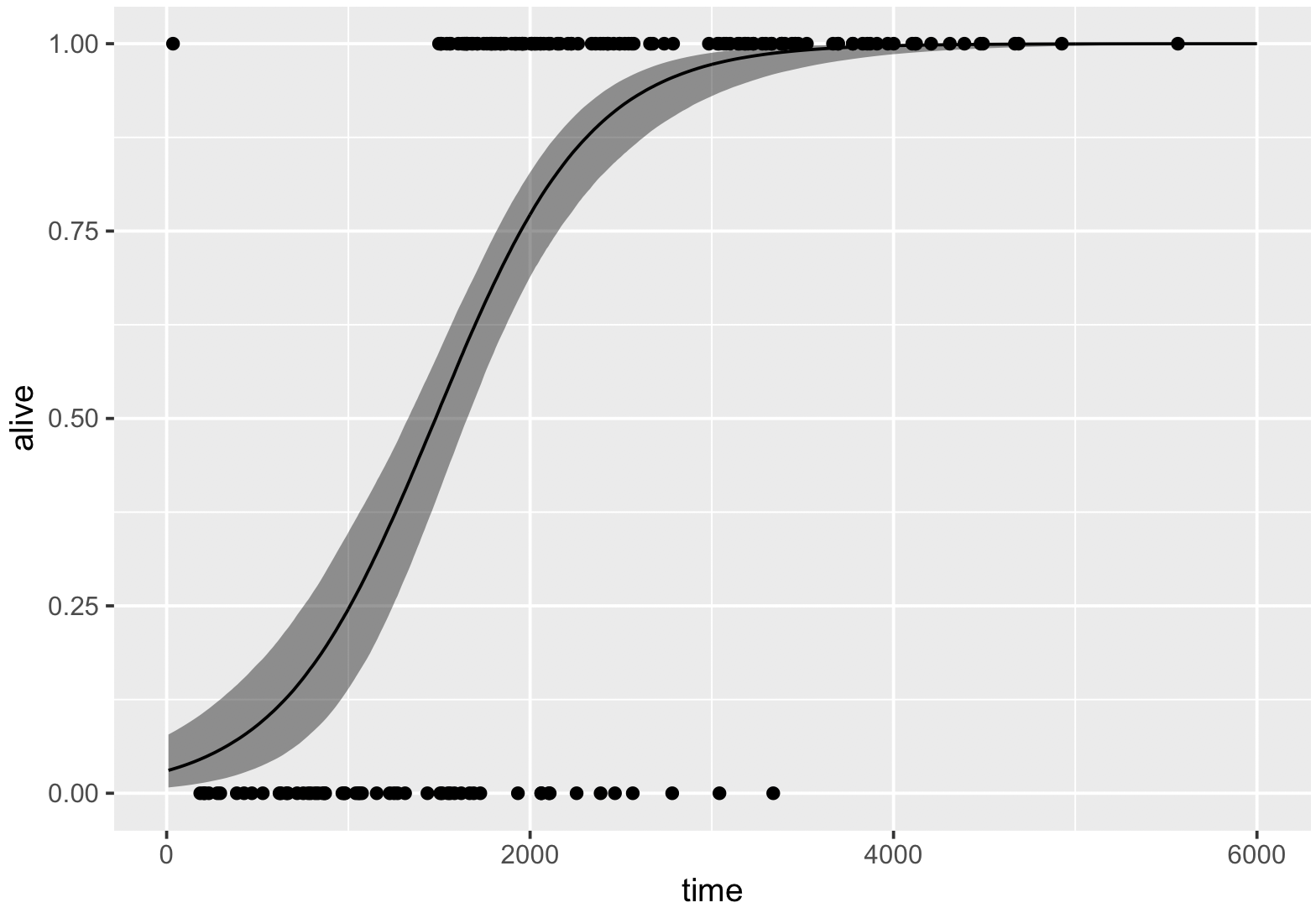
g <- ggplot(df.pred, aes(x = x))
g <- g + geom_ribbon(aes(ymin = lower, ymax = upper), fill = '#000000', alpha = 0.4)
g <- g + geom_line(aes(y = median))
g <- g + geom_point(data = data.frame(x = x, y = y), aes(x = x, y = y))
g <- g + xlab('time') + ylab('alive')
print(g)