ポアソン回帰はカウントデータあるいはイベントの発生率をモデル化する際に用いられる。このページでは、Stan を使ってポアソン回帰モデルのパラメーター推定を行う方法を示す。データとして、ガラパゴス島に生息している動物の種数データを使用して、島の面積とその島で生息している動物の種数を、ポアソン回帰でモデル化する例を示す。なお、このデータセットは R の faraway パッケージに保存されている。

data(gala, package = 'faraway')
head(gala)
##              Species Endemics  Area Elevation Nearest Scruz Adjacent
## Baltra            58       23 25.09       346     0.6   0.6     1.84
## Bartolome         31       21  1.24       109     0.6  26.3   572.33
## Caldwell           3        3  0.21       114     2.8  58.7     0.78
## Champion          25        9  0.10        46     1.9  47.4     0.18
## Coamano            2        1  0.05        77     1.9   1.9   903.82
## Daphne.Major      18       11  0.34       119     8.0   8.0     1.84

plot(log10(gala$Area), gala$Species, xlab = 'log10(Area)', ylab = 'Species')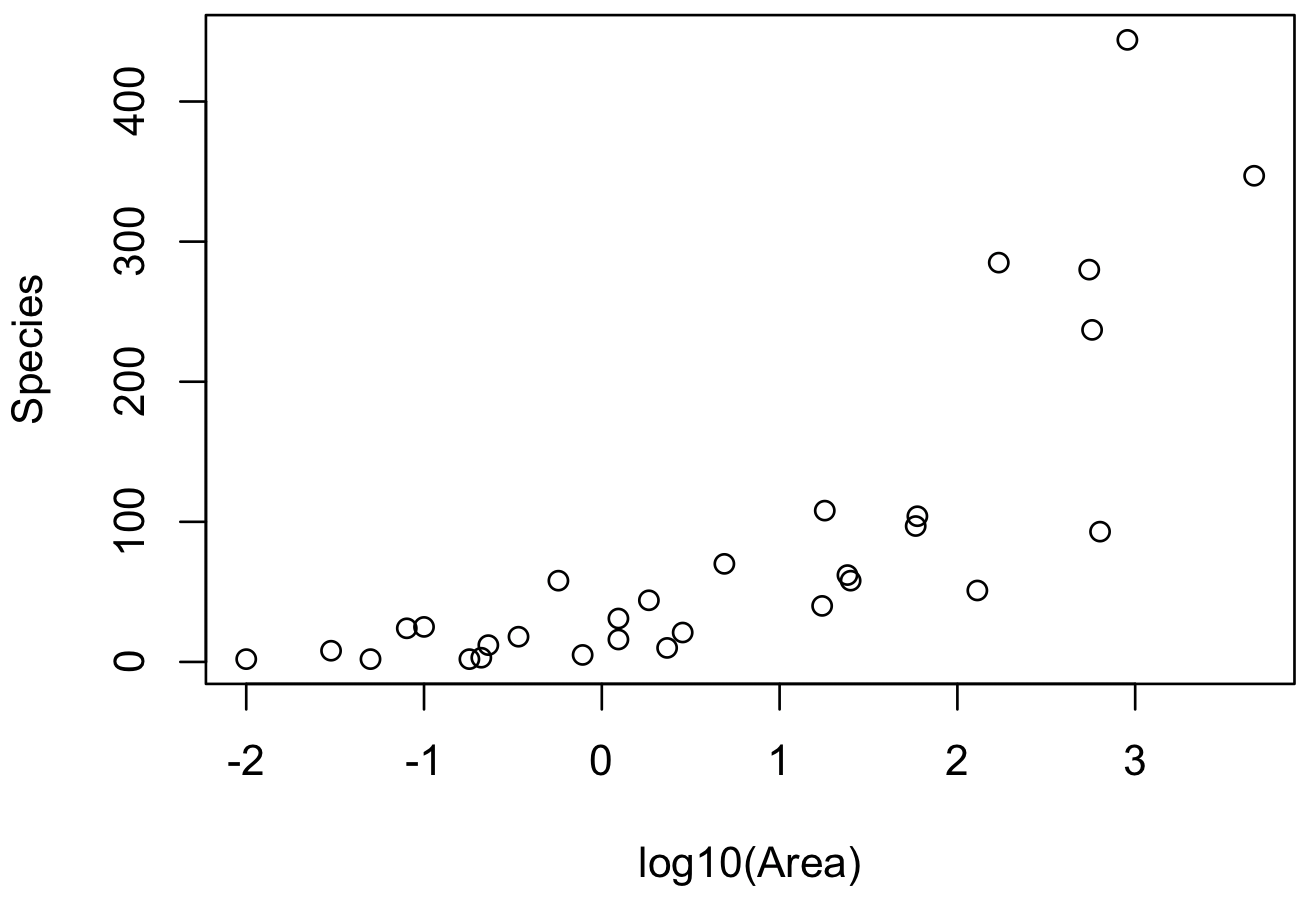

次に、Stan コードを使用して、ポアソン回帰を記述していく。Stan のコードでは、まず、島の面積 x と種数 y のデータを受け取るように data ブロックで定義する。次に、ポアソン回帰のパラメーターとして β₀ および β₁ を parameters ブロックで定義する。ただし、これらのパラメーターが、そのままポアソン回帰に用いられるのではなく、次のようにリンク関数で、変換されてからポアソン回帰モデルに代入される。

そこで、Stan コードの transformed parameters ブロックで、パラメーター β₀ および β₁ を λ に変換するように制御する。この変換を行った後に、λ を使って、model ブロックで、ポアソン分布からサンプリングを行なう。また、パラメーターを推定した後に、島の面積が 1〜5 の範囲にあるときの種数の予測区間も計算したいので、続いて generated quantities ブロックで再サンプリングを行うようにする。

data {
    int N;
    real x[N];
    int y[N];

    int new_N;
    real new_x[new_N];
}
parameters {
    real beta_0;
    real beta_1;
}
transformed parameters {
    real lambda[N];
    for (n in 1:N) {
        lambda[n] = exp(beta_0 + beta_1 * x[n]);
    }
}
model {
    y ~ poisson(lambda);
}
generated quantities {
    real muhat[new_N];
    real yhat[new_N];

    for (i in 1:new_N) {
        muhat[i] = exp(beta_0 + beta_1 * new_x[i]);
        yhat[i] = poisson_rng(muhat[i]);
    }
}

R を使用してデータを代入しポアソン回帰モデルのパラメーター推定を行う。ただし、島の面積のスケールが大きいので、対数化を行なう。データをそのまま対数化すると、島の面積にマイナスの値が生じるので、ここで島の面積の単位を km² から m² に変換してから対数化を行なう。

library(rstan)
x <- log10(gala$Area * 1000000)
y <- gala$Species
new.x <- seq(1, 10, 0.1)

d <- list(x = x, y = y, N = length(x), new_x = new.x, new_N = length(new.x))
fit <- stan(file = 'pois.stan', data = d)
fit
## Inference for Stan model: pois.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
##                mean se_mean    sd     2.5%      25%      50%      75%    97.5%  n_eff  Rhat
## beta_0        -1.40    0.01  0.14    -1.69    -1.49    -1.40    -1.30    -1.14    750  1.01
## beta_1         0.78    0.00  0.02     0.75     0.77     0.78     0.79     0.81    753  1.01
## lambda[1]     78.31    0.05  1.93    74.65    76.98    78.28    79.61    82.22   1404  1.00
## lambda[2]     28.33    0.04  1.17    26.05    27.53    28.30    29.10    30.65    870  1.01
## lambda[3]     15.54    0.03  0.82    13.94    14.99    15.51    16.10    17.17    811  1.01
## ...
## lambda[28]    32.37    0.04  1.25    29.92    31.51    32.34    33.21    34.85    792  1.01
## lambda[29]    28.33    0.04  1.17    26.05    27.53    28.30    29.10    30.65    752  1.01
## lambda[30]    37.53    0.04  1.35    34.89    36.59    37.50    38.45    40.21    798  1.01
## muhat[1]       0.54    0.00  0.07     0.41     0.49     0.54     0.58     0.68    752  1.00
## muhat[2]       0.58    0.00  0.07     0.45     0.53     0.58     0.63     0.73    791  1.00 
## muhat[3]       0.63    0.00  0.07     0.49     0.58     0.63     0.68     0.79    792  1.00
## ...
## muhat[39]     10.35    0.02  0.63     9.11     9.93    10.32    10.78    11.60    772  1.00
## muhat[40]     11.19    0.02  0.66     9.89    10.74    11.16    11.64    12.51    771  1.00
## muhat[91]     12.10    0.02  0.70    10.72    11.62    12.07    12.57    13.48    784  1.00
## yhat[1]        0.53    0.01  0.74     0.00     0.00     0.00     1.00     2.00   3561  1.00
## yhat[2]        0.58    0.01  0.75     0.00     0.00     0.00     1.00     2.00   3561  1.00
## yhat[3]        0.64    0.01  0.79     0.00     0.00     0.00     1.00     3.00   3624  1.00 
## ...
## yhat[39]      10.38    0.05  3.25     4.00     8.00    10.00    12.00    17.00   3543  1.00
## yhat[40]      11.12    0.06  3.38     5.00     9.00    11.00    13.00    18.00   3884  1.00
## yhat[91]      12.18    0.06  3.52     6.00    10.00    12.00    14.00    19.00   3353  1.00
## lp__       10238.36    0.04  1.01 10235.73 10237.94 10238.67 10239.09 10239.37    803  1.00

ms <- rstan::extract(fit, pars = 'yhat')
dim(ms$yhat)
## [1] 4000  91

df.pred <- data.frame(x = new.x,
                      lower  = apply(ms$yhat, 2, quantile, prob = 0.025),
                      median = apply(ms$yhat, 2, quantile, prob = 0.500),
                      upper  = apply(ms$yhat, 2, quantile, prob = 0.925))
g <- ggplot(df.pred, aes(x = x))
g <- g + geom_ribbon(aes(ymin = lower, ymax = upper), fill = '#000000', alpha = 0.4)
g <- g + geom_line(aes(y = median))
g <- g + geom_point(data = data.frame(x = x, y = y), aes(x = x, y = y))
g <- g + xlab('log10(Area)') + ylab('Species')
print(g)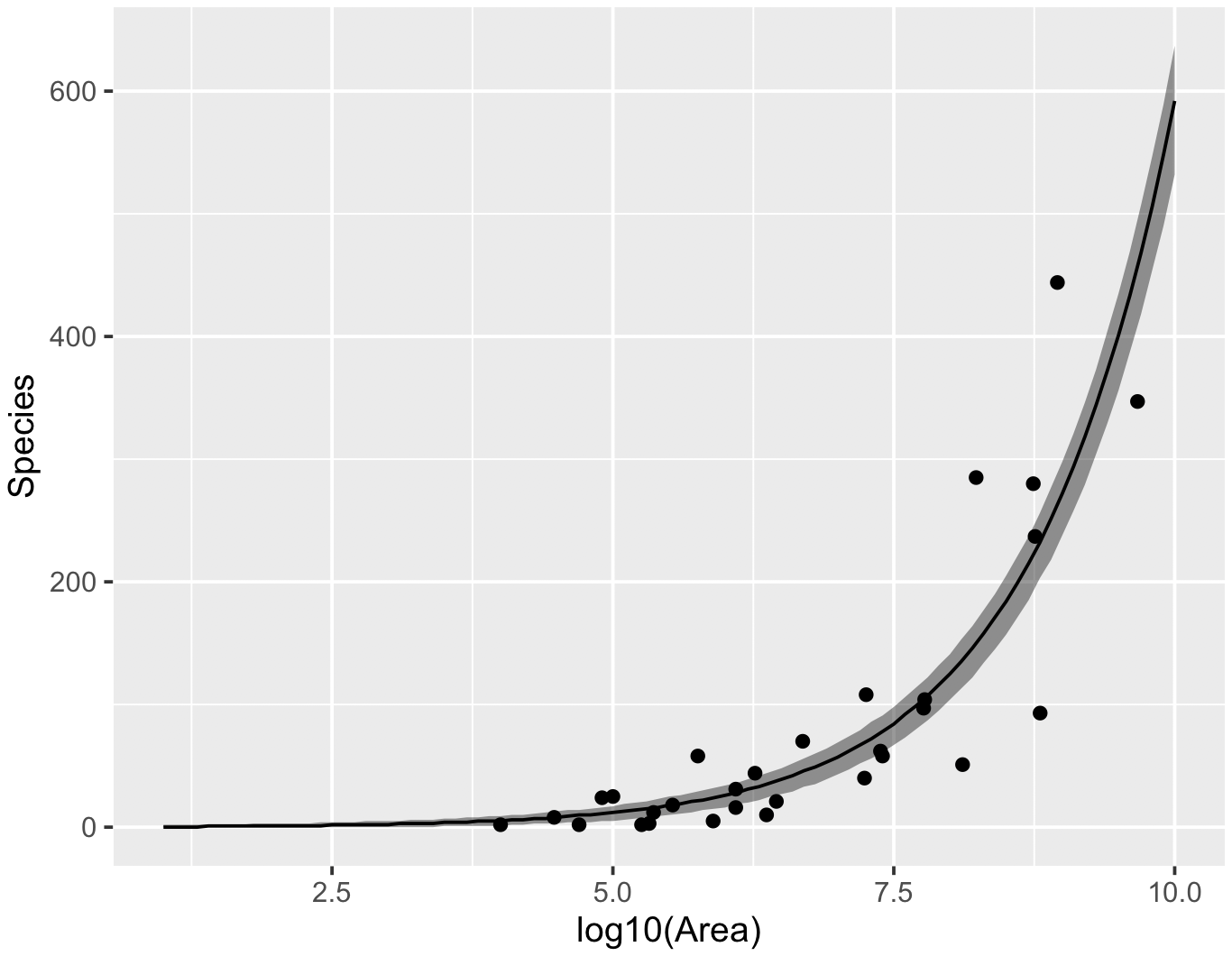

95% 予測区間を確認すると、大部分の観測点が、予測区間の外側にあることが確認できる。このデータをポアソン回帰でモデリングすると過分散を起こしているのを確認できる。ポアソン回帰よりも大きな分散を許容できる負の二項回帰を検討した方がいいかもしれない。

poisson_log

ポアソン回帰のとき、Stan コードにおいて exp と poisson を同時に使うと計算が不安定になる。そのため、ポアソン回帰を行う時、の 2 つの関数を組み合わせて利用するのではなく、poisson_log 関数を使うことが推奨されている。poisson_log 関数を利用する場合は、次のように変数変換を行う。ただし、poisson_log 関数を使用する場合も、モデリングに失敗する場合がある。 \[ \lambda_{i} = \beta_0 + \beta_1 x \] \[ y_{i} \sim PoissonLog(\lambda_{i}) \]

このとき Stan コードでは次のようにしてモデルを記述する。

data {
    int N;
    real x[N];
    int y[N];
}
parameters {
    real beta_0;
    real beta_1;
}
transformed parameters {
    real lambda[N];
    for (n in 1:N) {
        lambda[n] = beta_0 + beta_1 * x[n];
    }
}
model {
    y ~ poisson_log(lambda);
}
generated quantities {
  real yhat[N];
  yhat = poisson_log_rng(lambda);
}