太陽の黒点は 11 年周期で増減していることが知られている。ここで Stan を使って、このような周期性を持つ時系列データ用いて、状態空間モデルを構築し、そのパラメーターを推定する方法を示す。太陽の黒点データセットは R の sunspot.year オブジェクトに保存されている。このデータセットには下図のように 289 年分のデータが含まれているが、ここでは最初の 50 年分だけを使ってモデルを構築してみる。
data(sunspot.year)
plot(sunspot.year)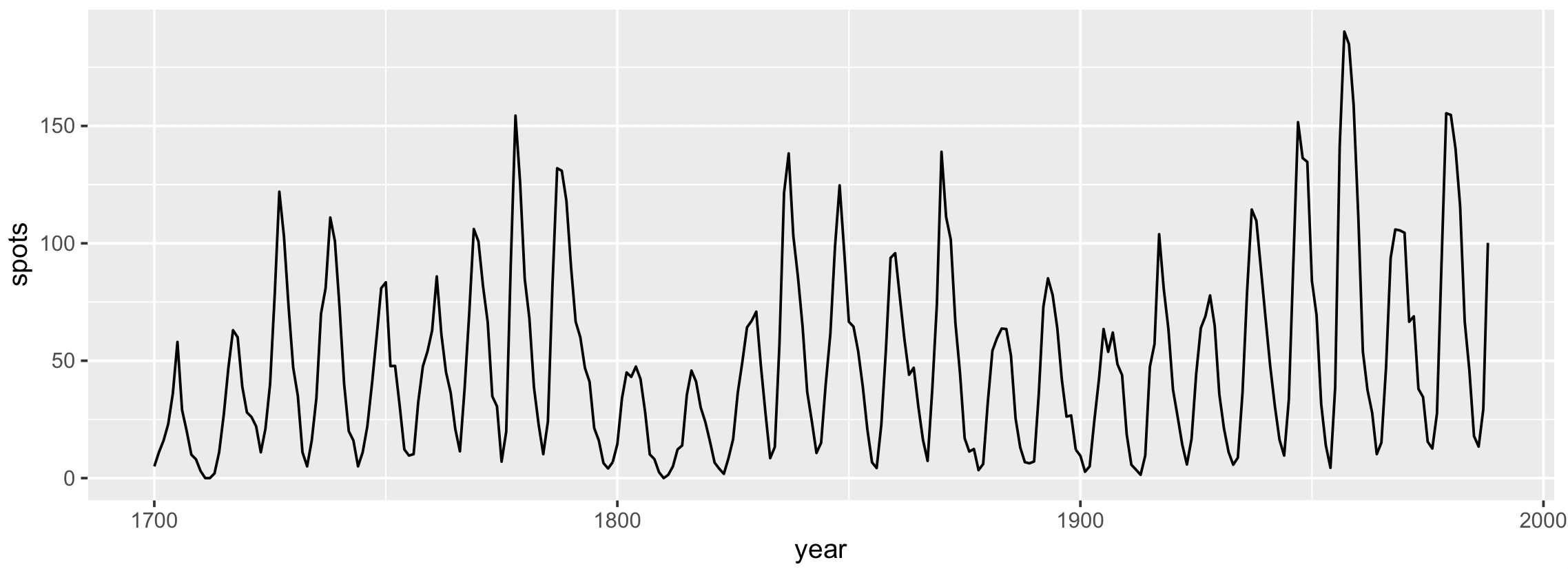
状態空間モデルの方程式
状態空間モデルでは、状態と観測値の 2 つの変数で構成されれ、時系列データが定常性を持つとき、t 時点で観測される観測値 yt は状態 xt から生成されるとされる。そして、状態 xt は、状態 xt-1 のみに依存して定まる。周期性を持つ時系列データの場合は、周期性を取り除くことで、t 時点で観測される観測値 yt は状態 xt から生成されると考えることができる。言い換えれば、t 時点において状態 xt に周期変動 pt を加えた値に、さらに観測ノイズ εt が加わり、観測値 yt が生成されると考えることができる。
\[ y_{t} = x_{t} + p_{t} + \epsilon_{y,t} \]状態 xt は、状態 xt-1 のみに依存するので、次のよう書き表すことができる。
\[ x_{t} = x_{t-1} + \epsilon_{x,t} \sim \mathcal{N}\left(x_{t-1}, \sigma_{x}\right) \]周期変動について、11 年分の変動の和を見たとき、どの 11 年分でも平均 μp および標準偏差 σp になると考えられる。そこで、その平均に定数 μp だけ引けば、11 年分の変動の和が平均 0 および標準偏差 σp になる。これを式で表すと、
\[ p_{t} + p_{t+1} + \cdots p_{t+10} = \sum_{i=0}^{10} p_{t-i} = \epsilon_{p, t} \sim \mathcal{N}\left(0, \sigma_{p}\right) \]この式を pt について展開すると、
\[ p_{t} = - \sum_{i=1}^{10}p_{t-i} + \epsilon_{p, t} \sim \mathcal{N}\left(- \sum_{i=1}^{10}p_{t-i}, \sigma_{p}\right) \]pt の方程式ができたので、これを観測方程式に代入して、観測値 yt の方程式は次のように書き表わせる。
\[ y_{t} = x_{t} + p_{t} + \epsilon_{y,t} \sim \mathcal{N}\left( x_{t}+p_{t}, \sigma_{y} \right) \]Stan コード
上で求めた、状態方程式、周期変動に関する方程式、観測方程式を Stan コードで記述していく。for 文で記述すると、実行速度が非常に遅いので、必要に応じてベクトル化した方がいい。
data {
int N;
vector[N] Y;
}
parameters {
vector[N] mu;
vector[N] period;
real<lower=0> sigma_mu;
real<lower=0> sigma_period;
real<lower=0> sigma_Y;
}
transformed parameters {
vector[N] y_mean;
y_mean = mu + period;
}
model {
// // state equation
for (i in 2:N) {
mu[i] ~ normal(mu[i - 1], sigma_mu);
}
// mu[2:N] ~ normal(mu[1:(N - 1)], sigma_mu);
// seasonal effects
for (i in 11:N) {
period[i] ~ normal(-sum(period[(i - 10):(i - 1)]), sigma_period);
}
// observation equation
for (i in 1:N) {
Y[i] ~ normal(y_mean, sigma_Y);
}
// Y ~ normal(y_mean, sigma_Y);
}パラメーター推定
太陽の黒点データ(sunspot.year)の最初の 50 年分だけのデータを使って、モデルパラメーターを推測してみる。続いて、推測されたパラメーターの期待値(平均値)およびその 95% 信頼区間を図示する。
library(rstan)
n <- 50
d <- list(Y = as.numeric(sunspot.year)[1:n], N = n)
fit <- stan(file = "sunspot.stan", data = d)
ms <- rstan::extract(fit, pars = c('mu', 'period', 'y_mean'))
df <- data.frame(x = time(sunspot.year)[1:n],
y = as.numeric(sunspot.year)[1:n],
lower = apply(ms$y_mean, 2, quantile, prob = 0.025),
median = apply(ms$y_mean, 2, quantile, prob = 0.500),
upper = apply(ms$y_mean, 2, quantile, prob = 0.925))
g <- ggplot(df, aes(x = x, y = y, ymin = lower, ymax = upper))
g <- g + geom_ribbon(fill = '#000000', alpha = 0.4, data = df)
g <- g + geom_point()
g <- g + xlab('year') + ylab('spots')
print(g)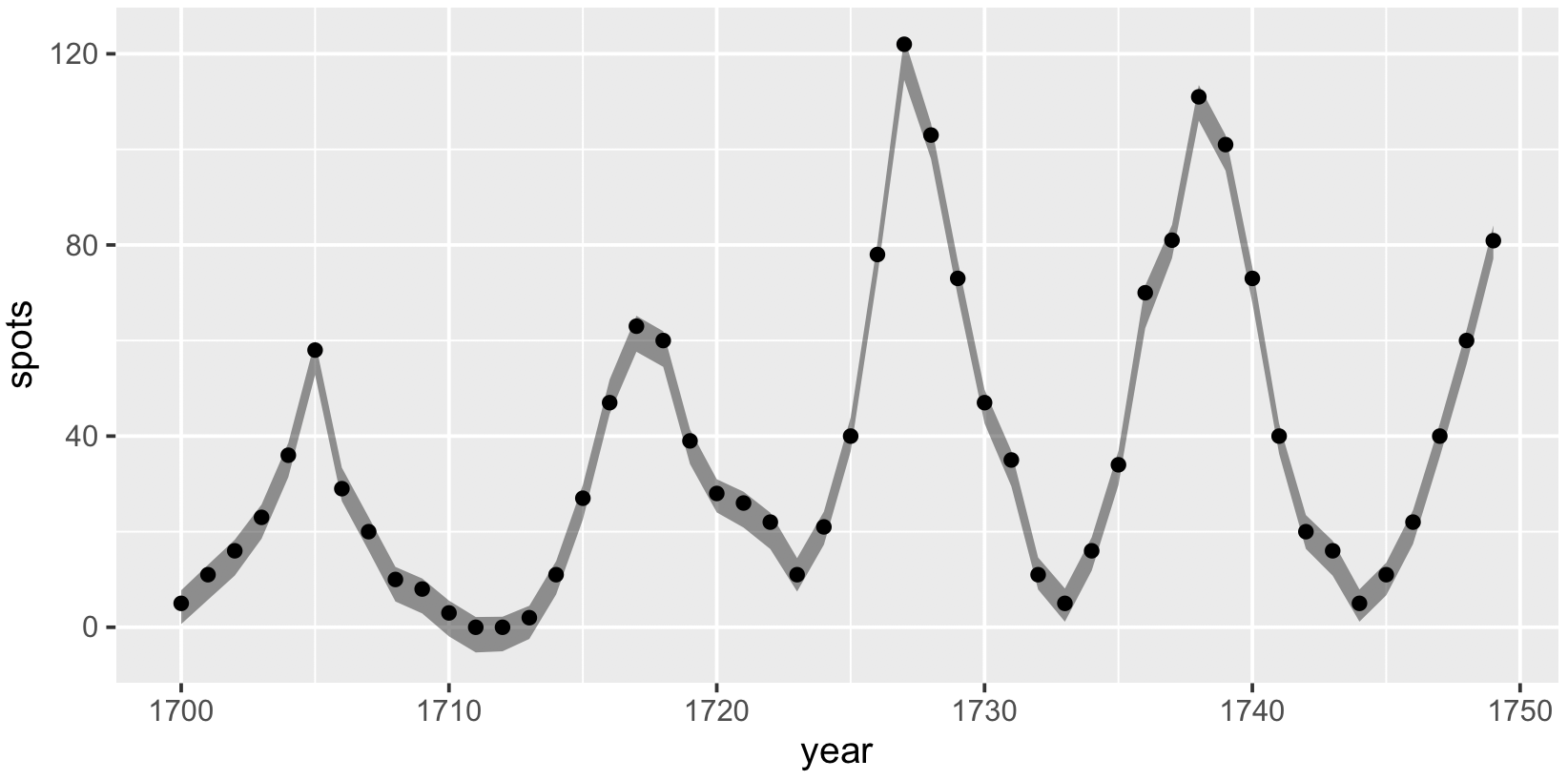
推定された周期変動項は次のようになっている。灰色は 95% 信頼区間である。
library(rstan)
n <- 50
d <- list(Y = as.numeric(sunspot.year)[1:n], N = n)
fit <- stan(file = "sunspot.stan", data = d)
ms <- rstan::extract(fit, pars = c('mu', 'period', 'y_mean'))
df <- data.frame(x = time(sunspot.year)[1:n],
lower = apply(ms$period, 2, quantile, prob = 0.025),
median = apply(ms$period, 2, quantile, prob = 0.500),
upper = apply(ms$period, 2, quantile, prob = 0.925))
g <- ggplot(df, aes(x = x, y = median, ymin = lower, ymax = upper))
g <- g + geom_ribbon(fill = '#000000', alpha = 0.4, data = df)
g <- g + geom_line()
g <- g + xlab('year') + ylab('period')
print(g)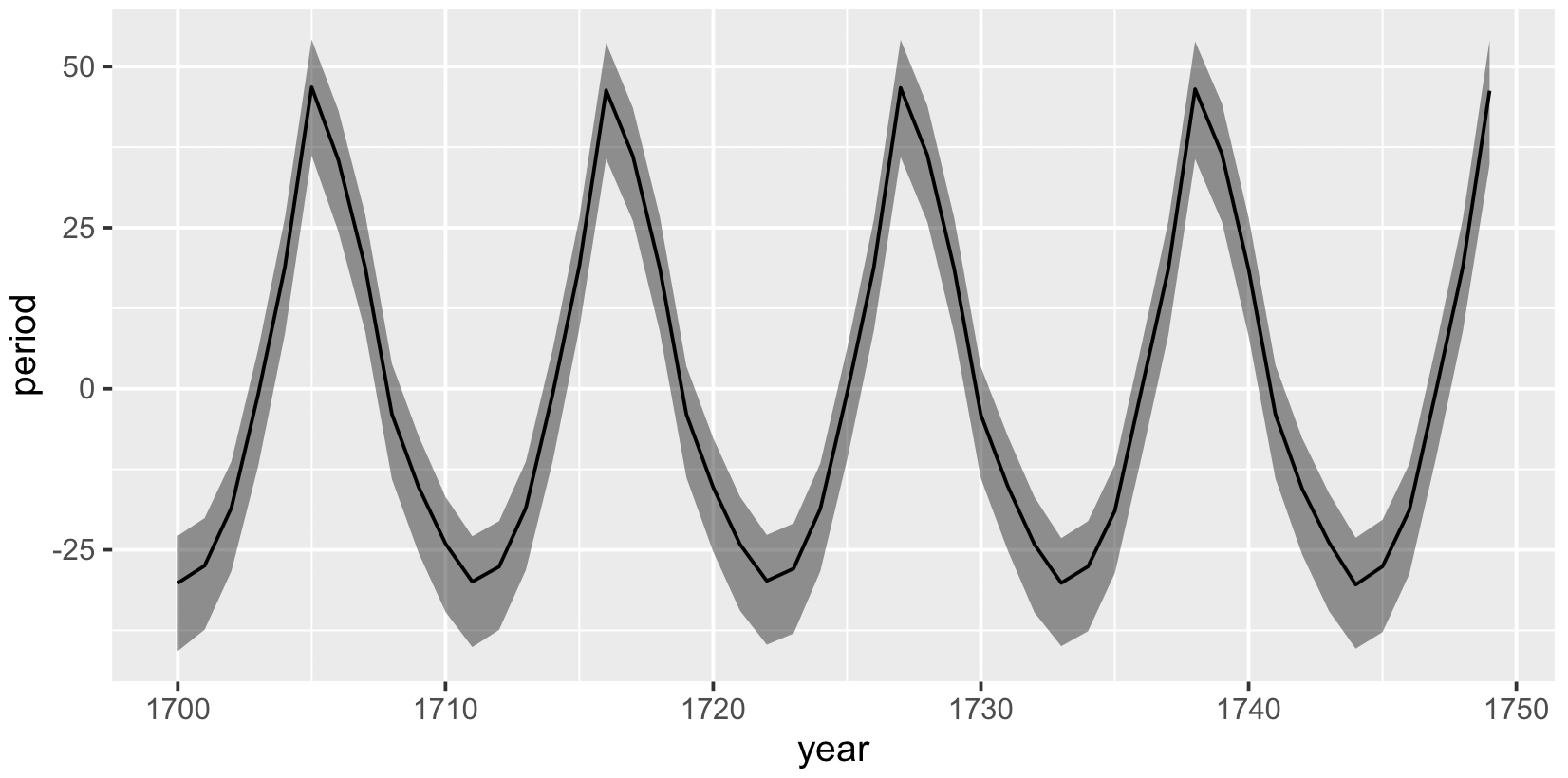
References
- Stan と R でベイズ統計モデリング. 共立出版