現在の状態（確率変数） X_n が与えられたとき、X_{n + 1} は X_n だけで決定され、過去のいかなる状態（X₀, X₁, ..., X_{n - 1}）とも無関係である。このような性質をマルコフ性という。これを数式で表すと次のようになる。

ある状態 X_i から別の状態 X_j に確率 p(X_n, X_{n + 1}) で遷移するとき、確率 p(X_n, X_{n + 1}) がマルコフ性を持つならば、その確率過程をマルコフ過程という。ある状態 X_i から別の状態 X_j に遷移する確率 p は、状態遷移確率行列で表されることが多い。マルコフ過程において、確率変数が離散的な値をとるとき、これをマルコフ連鎖という。

マルコフ連鎖の具体例を取り上げてみる。子供の 1 日をマルコフ連鎖で表すことについて考えてみる。子供の 1 日は、寝る、遊ぶ、食べる、泣くの 4 つの行動からなるとする。子供を行動を記録して、子供が一定時間寝た後に、0.2 の確率の遊び、0.1 の確率で食べ物を食べ、0.2 の確率で泣き、0.5 の確率でもう一度寝ることがわかったとする。また、一定時間遊んだ子供が、次に、それぞれ 0.3, 0.3, 0.3, 0.1 の確率で遊ぶ、寝る、食べる、泣くとする。このように寝る、遊ぶ、食べる、泣くの 4 つの行動が遷移する確率をすべて求める。これらの確率を図で示すと次のようになる。

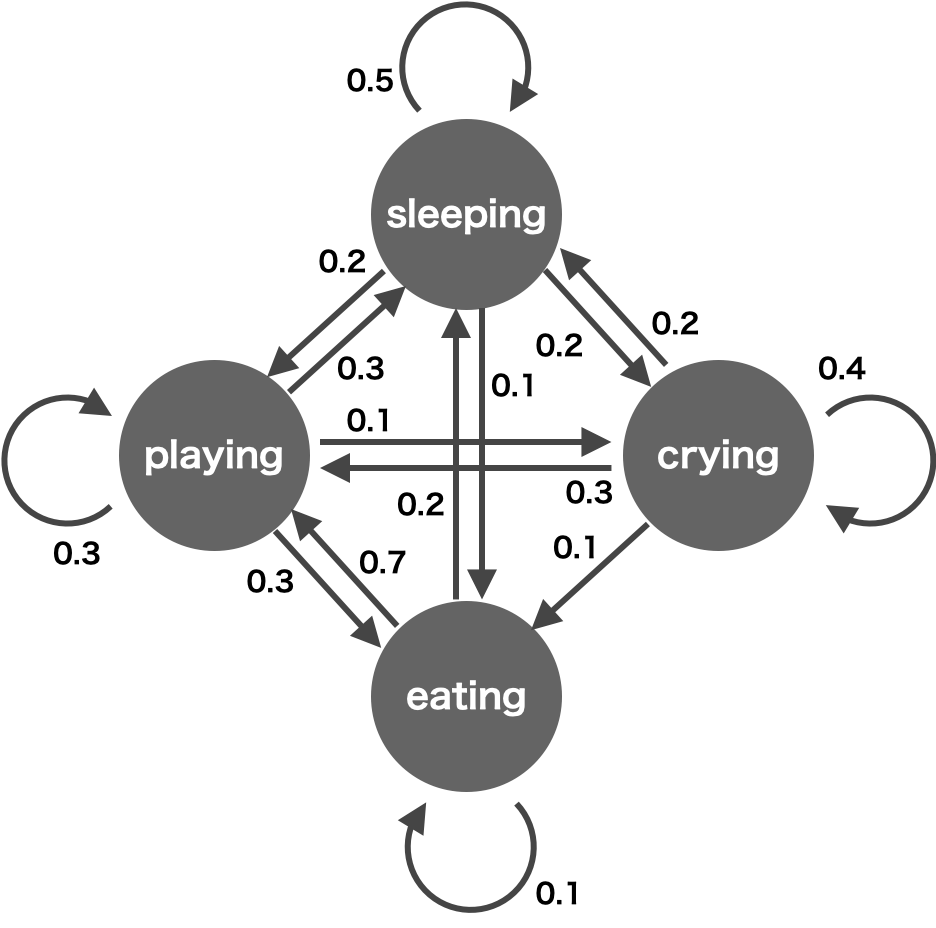
このマルコフ連鎖の状態遷移図を使用すれば、例えば、次のような子供の 1 日をシミュレートできるようになる。

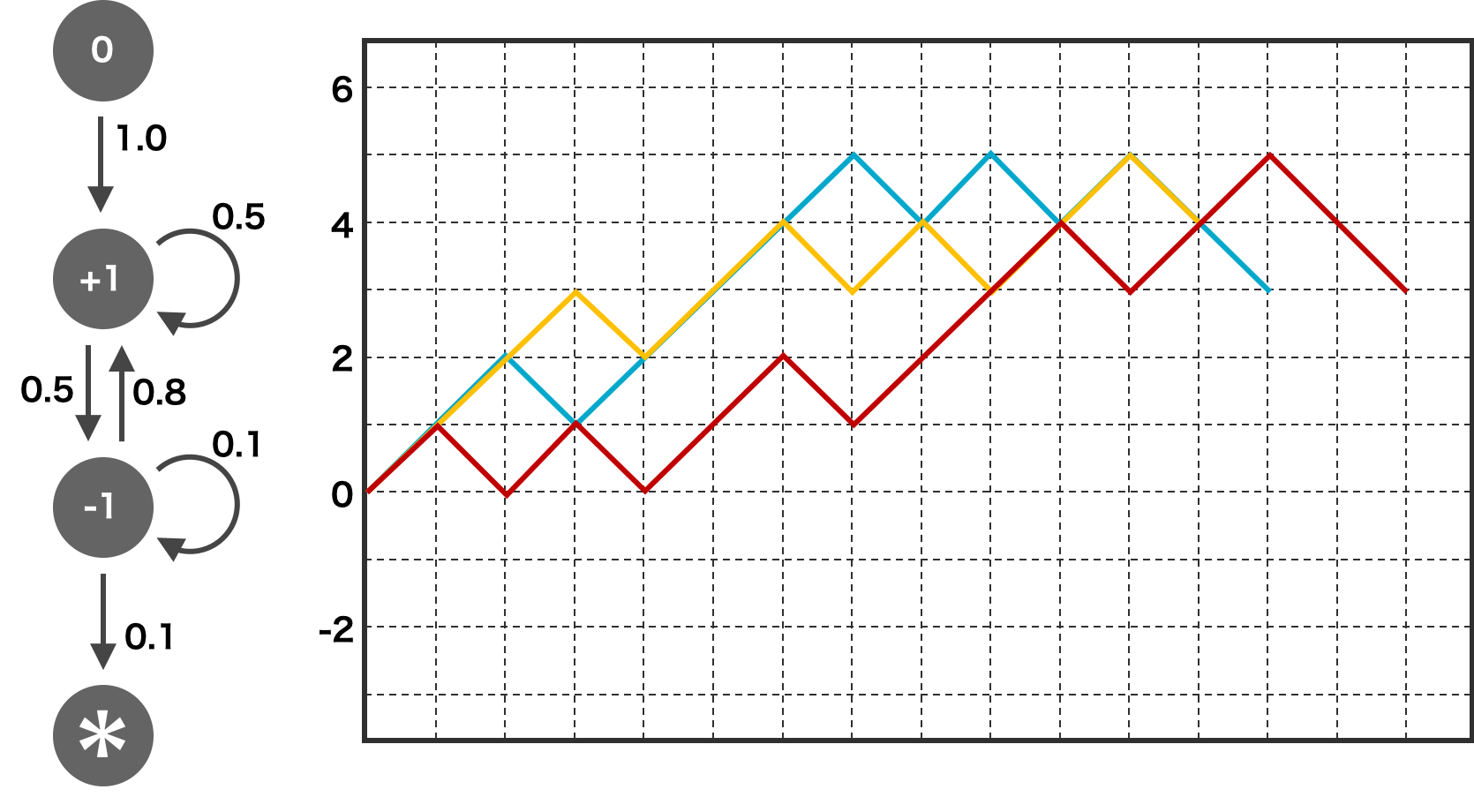
また、マルコフ連鎖を使用して乱数を生成することもできる。例えば、下図のように乱数を生成するルールを状態遷移図で書き、その状態遷移図に従えば、乱数を生成できるようになる。下図の例では、乱数を 3 セット生成していることを示している。

red:    0, 1, 0, 1, 0, 1, 2, 1, 2, 3, 4, 3, 4, 5, 4, 2, *
blue:   0, 1, 2, 1, 2, 3, 4, 5, 4, 5, 4, 5, 4, 3, *
orange: 0, 1, 2, 3, 2, 3, 4, 3, 4, 3, 4, 5, 4, *