モンテカルロ法は、複雑な数値計算を、乱数を用いて近似解を求める方法の総称である。例えば、ベイズ推定ではパラメータ数が多くなると、ベイズ推定式の分母の積分計算が非常に複雑になり、解けなくなる。このとき、分母の積分を正確に解く代わりに、乱数を使って近似解を求める方法が取られている。

関数 f(x) を区間 [a, b] で積分することを考える。f(x) の関数式が簡単であれば、これを数学的に積分して、正確な値を求めればよい。しかし、f(x) の式が複雑であれば、数学的に積分することが非常に困難になる。このときに、モンテカルロ法による積分が行われる。

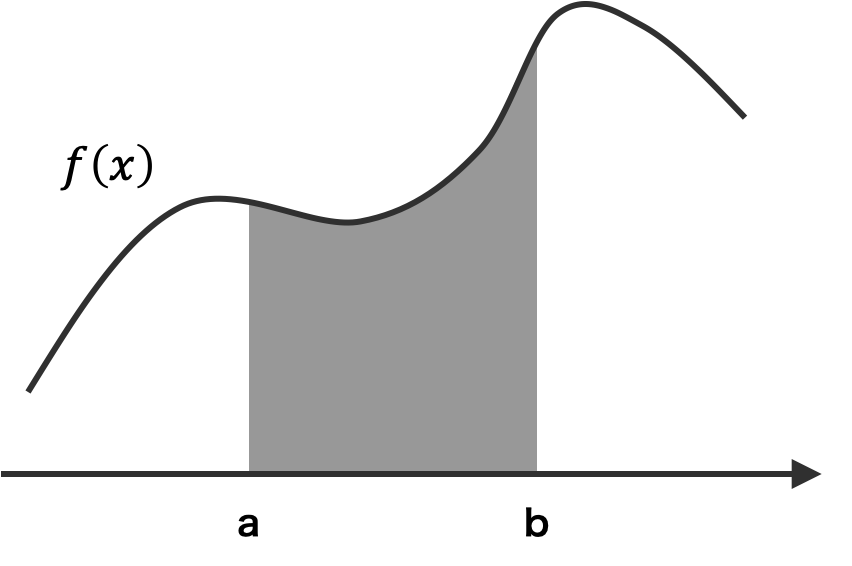
積分の基礎概念から積分について考えて、乱数で積分計算を行っていく。まず、区間 [a, b] を n 個の部分区間に等分割する。例えば、n = 15 個の部分区間に等分割する。次に、それぞれの部分区間の中心の座標を x₁, x₂, ..., x₁₅ とおく。すると、それぞれの部分区間は、幅 (b-a)/n、高さ f(x_i) の長方形にみえる。このとき、区間 [a, b] における f(x) の積分は、この n = 15 個の長方形の面積の和に近似できる。

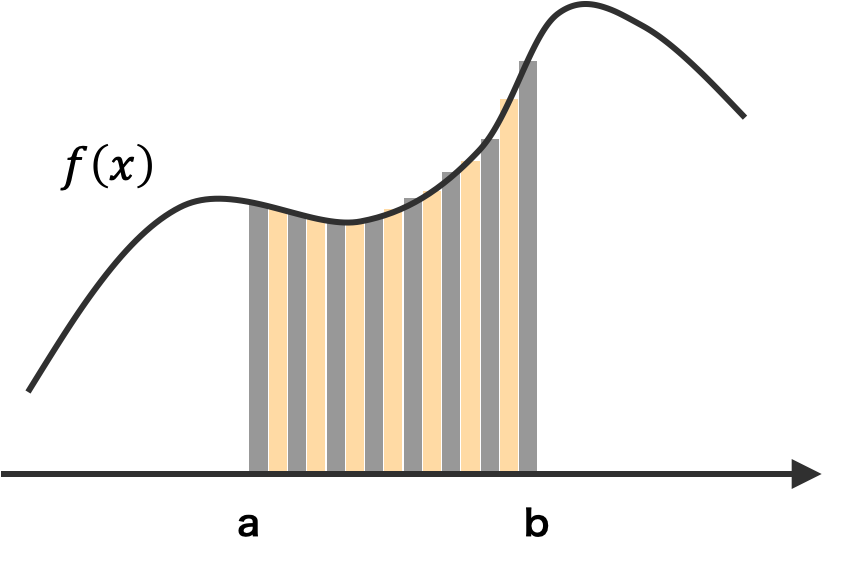
区間 [a, b] を n = 15 分割したときに得られる長方形を f(x) に当てはめると、長方形が f(x) を超えたり、f(x) よりも小さかったりする。つまり、長方形の面積の和と f(x) の [a, b] における面積との間に大きな誤差が含まれている。そこで、n を増やしてみる。このとき、数のように、長方形を f(x) に当てはめたときのばらつきが小さくなった。

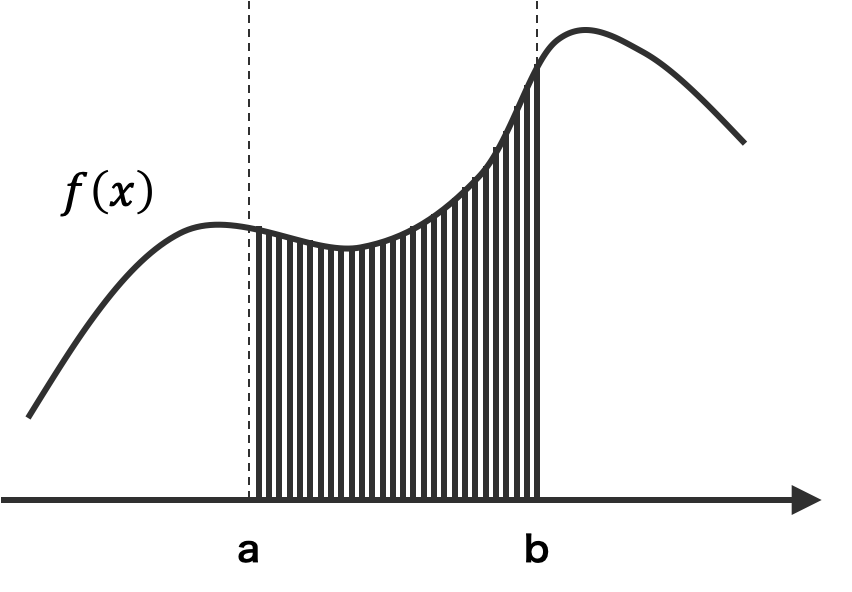
さらに n を増やすと、長方形がほぼ f(x) にフィットできるようになる。このときに、長方形の面積の和を計算すれば、その和が f(x) の区間 [a, b] における積分と非常に近くなる。

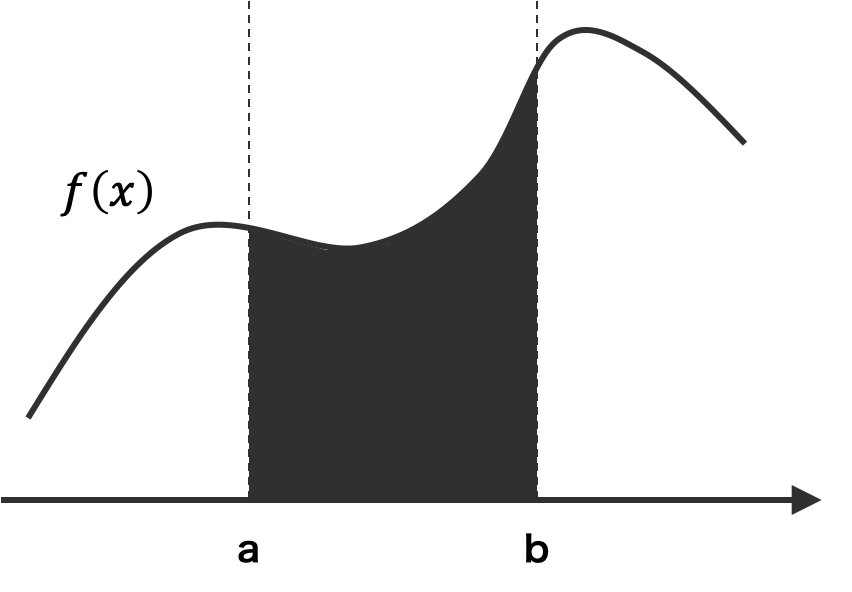
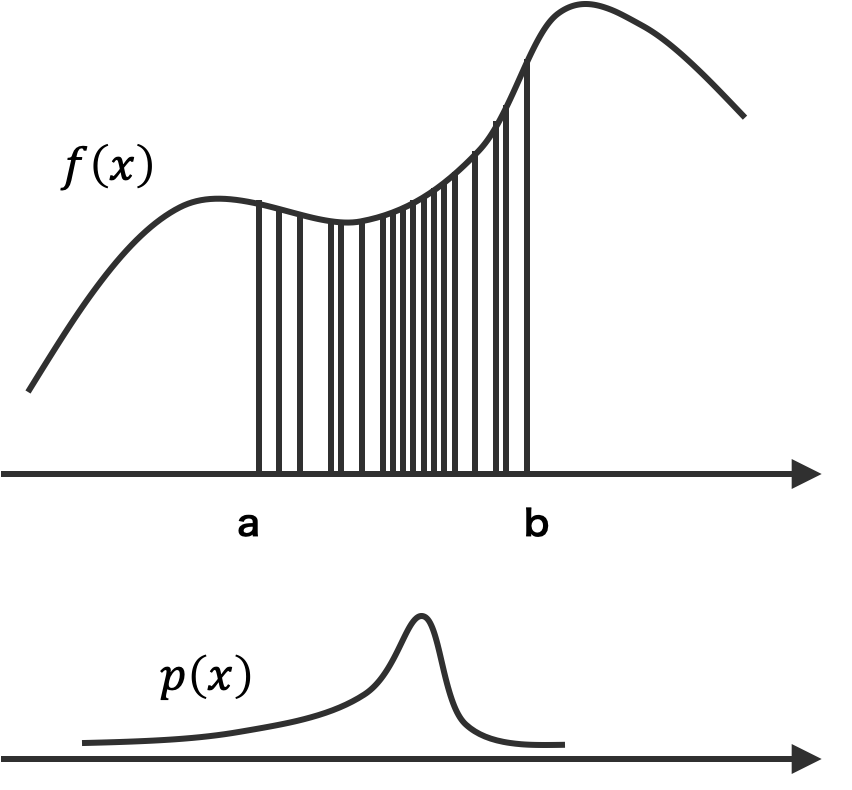
n が十分大きければ、区間 [a, b] を n 個の部分区間に等分割する必要がなく、区間 [a, b] の一様分布からランダムに n 個のサンプル x₁, x₂, ..., x_n を抽出して、サンプル 1 つを一つの長方形と見なすこともできる。このときも、次式が成り立つ。モンテカルロ法による積分では、このような考えのもとで積分計算を行っている。

ここまでの説明は、区間 [a, b] から n 個の部分区間に等分割する、あるいは区間 [a, b] の一様分布から n 個のサンプルを抽出して積分計算を行った。実際に、一様分布から n 個のサンプルを抽出するのではなく、他の確率分布から n 個のサンプルを抽出しても同じように積分できる。ただし、その際に、各長方形の横幅が同じでなくなるので、長方形の幅をその分布の確率密度関数 p(x) で補正する必要がある。