Stan 実行結果 | Stan の実行結果の見方とその図示

Stan(rstan) の実行結果は stanfit クラスのオブジェクトとして保存される。このオブジェクトの中には、MCMC サンプリングを行った時の条件や推定されたパラメーターの分布などが記録されている。このページでは、この stanfit クラスのオブジェクトかた必要なデータを取り出して、保存したり、図示したりする方法を示す。

Stan によるモデルパラメーター推定

ここで、テスト用に、R を使って平均 10 分散 4 となる正規分布に従う乱数を 100 個発生させて、次に Stan で乱数の生成元となる正規分布のパラメーターを推測して stanfit クラスのオブジェクトを作成する。

data {
    int n;
    real x[n];
}
parameters {
    real mu;
    real sigma;
}
model {
    x ~ normal(mu, sigma);
}

x <- rnorm(n = 100, mean = 10, sd = 2)
d <- list(x = x, n = length(x))
fit <- stan(file = 'normdisp.stan', data = d)
fit
## Inference for Stan model: tmp.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##          mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
## mu      10.25    0.00 0.19    9.88   10.13   10.25   10.38   10.63  3048    1
## sigma    1.90    0.00 0.13    1.66    1.80    1.89    1.98    2.17  2963    1
## lp__  -113.29    0.02 1.01 -116.08 -113.67 -112.98 -112.60 -112.32  1781    1

Stan 結果の取得

stan 関数によりモデル推定を行った結果が fit オブジェクトに保存されるため、パラメーターの推定結果を取得したい時、この fit オブジェクトの中から抽出する。

サンプリング条件

stanfit クラスのオブジェクトをそのまま表示させるか、または summary(fit) で表示させることによって、パラメーター推定結果の概要を見ることができる。例えば、次の場合、iter、warmup、および tihn にはそれぞれサンプリング回数、ウォームアップ回数、および間引き間隔を表す。

ウォームアップ回数は、サンプリング回数のうち、パラメーターに使われない最初の方のサンプリング回数を表す。サンプリング初期において、初期値から最適解付近に遷移するまでにステップ数がかかるために、ウォームアップを設けることで、その遷移過程を無視することになり、初期値の影響を軽減することができる。また、間引き間隔は、ウォームアップ後のサンプリング結果のうち、どのぐらいの間隔のものをパラメーター推定に使うのかを示している。例えば thin=2 とした場合は、パラメーター推定に使われるサンプリング結果は 1 回目、3 回目、5 回目、・・・の結果となる。

fit <- stan(file = 'normdisp.stan', data = d)
fit
## Inference for Stan model: tmp.
## 4 chains, each with iter=2000; warmup=1000; thin=1;
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##          mean se_mean   sd    2.5%     25%     50%     75%   97.5% n_eff Rhat
## mu      10.25    0.00 0.19    9.88   10.13   10.25   10.38   10.63  3048    1
## sigma    1.90    0.00 0.13    1.66    1.80    1.89    1.98    2.17  2963    1
## lp__  -113.29    0.02 1.01 -116.08 -113.67 -112.98 -112.60 -112.32  1781    1

fit オブジェクトから、Stan コードで記述されたモデルを取得することができる。この際に、get_stanmodel 関数を利用する。

ms <- rstan::extract(fit)

get_stanmodel(fit)
## S4 class stanmodel 'lm' coded as follows:
## data {
##     int n;
##     real x[n];
## }
## parameters {
##     real mu;
##     real sigma;
## }
## model {
##     x ~ normal(mu, sigma);
## }

初期化パラメーターおよびサンプリング時に使用したシードはそれぞれ get_inits と get_seeds 関数で取得できる。

ms <- rstan::extract(fit)

get_inits(fit)
## [[1]]
## [[1]]$mu
## [1] -1.676589
## [[1]]$sigma
## [1] 0.37793
## 
## [[2]]
## [[2]]$mu
## [1] -1.289332
## [[2]]$sigma
## [1] 1.433932
## 
## [[3]]
## [[3]]$mu
## [1] 1.719083
## [[3]]$sigma
## [1] 1.188696
## 
## [[4]]
## [[4]]$mu
## [1] -1.233047
## [[4]]$sigma
## [1] 0.2119928

get_seeds(fit)
## [1] 1469703516 1469703516 1469703516 1469703516

Rhat

各 Rhat について、chain 数が 3 以上のとき、すべてのパラメーターで Rhat < 1.1 ならば、MCMC サンプリングによるパラメーター推定が収束したとみなすことができる。

パラメーターの分布

各パラメーターに対する MCMC サンプリングの結果は extract 関数で取得できる。extract 関数で取得したサンプリング結果はリストの形で返される。リストの名前が、パラメーターの名前であり、リストの各要素がサンプリングの結果となる。上の例では、4 chains で、それぞれの chain では 1000 回サンプリングが行われたので、リストの各要素の長さが 4000 となっている。

ms <- rstan::extract(fit)

sapply(ms, length)
##    mu sigma  lp__
##  4000  4000  4000

sapply(ms, summary)
##                mu    sigma      lp__
## Min.     9.476039 1.517786 -120.6438
## 1st Qu. 10.125193 1.802569 -113.6709
## Median  10.248190 1.891605 -112.9778
## Mean    10.251277 1.897141 -113.2948
## 3rd Qu. 10.378800 1.980579 -112.5989
## Max.    10.917563 2.426028 -112.2946

extract 関数にはいくつかのオプションが用意されている。例えば、pars と include を組み合わせることで、特定のパラメーターだけを取り出せたり、あるいは特定のパラメーターだけを無視したりすることができる。

ms <- rstan::extract(fit, pars = c('mu', 'sigma'), include = TRUE)
names(ms)
## [1] "mu"    "sigma"

ms <- rstan::extract(fit, pars = c('mu', 'sigma'), include = FALSE)
names(ms)
## [1] "lp__"

また、ウォームアップの結果も含めたい場合は、inc_warmup オプションを利用する。ただし、この際に permuted=FALSE を指定する必要があり、このとき抽出されたデータは 3 次元配列として返される。

ms <- rstan::extract(fit, permuted = FALSE, inc_warmup = TRUE)
str(ms)
##  num [1:2000, 1:4, 1:3] -1.66 -1.66 -1.66 -1.66 -1.66 ...
##  - attr(*, "dimnames")=List of 3
##   ..$ iterations: NULL
##   ..$ chains    : chr [1:4] "chain:1" "chain:2" "chain:3" "chain:4"
##   ..$ parameters: chr [1:3] "mu" "sigma" "lp__"

対数事後確率の分布

ベイズ推定において、MCMC サンプリングにより、対数事後確率

\[ \log p(\theta | x) \propto \log p(x|\theta) + \log p(\theta) + C \]

の高いところでパラメーター探索を行われる。このときの対数事後確率は、lp__ の名前でパラメーターとして stanfit クラスのオブジェクトに保存される。そのため、他のモデルパラメーターと同様に、extract 関数で取得することができる。

ms <- rstan::extract(fit)
names(ms)
## [1]    mu sigma  lp__

sapply(ms, summary)
##                mu    sigma      lp__
## Min.     9.476039 1.517786 -120.6438
## 1st Qu. 10.125193 1.802569 -113.6709
## Median  10.248190 1.891605 -112.9778
## Mean    10.251277 1.897141 -113.2948
## 3rd Qu. 10.378800 1.980579 -112.5989
## Max.    10.917563 2.426028 -112.2946

ベイズ信頼区間

MCMC サンプリング結果がから各パラメーターのベイズ信頼区間を求めることができる。例えば、mu と singma の 95% 信頼区間は次のように求めることができる。

ms <- rstan::extract(fit)
quantile(ms$mu, probs = c(0.025, 0.975))
##      2.5%     97.5%
##  9.882575 10.632519

quantile(ms$sigma, probs = c(0.025, 0.975))
##     2.5%    97.5%
## 1.663189 2.174985

Stan 結果の図示

Stan の結果の図示は、extract 関数で取得できるため、取得した値を使用してヒストグラムなどを描くことができる。このほかに、rstan パッケージで用意された関数を使ってグラフを描くこともできる。各回の MCMC サンプリングによってパラメーターの値がどのように遷移したのかを確認したい場合は、stan_trace 関数を使うことで図示できる。

stan_trace(fit)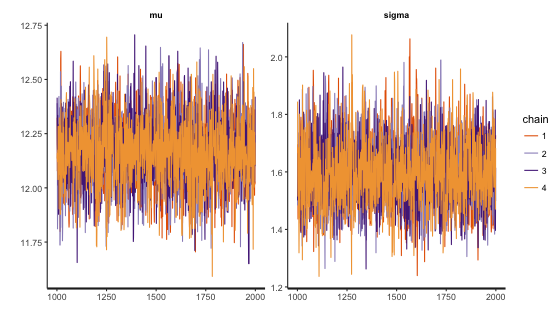

また、推定されたパラメーターの分布（ヒストグラム）は stan_hist 関数を使用する。

stan_hist(fit)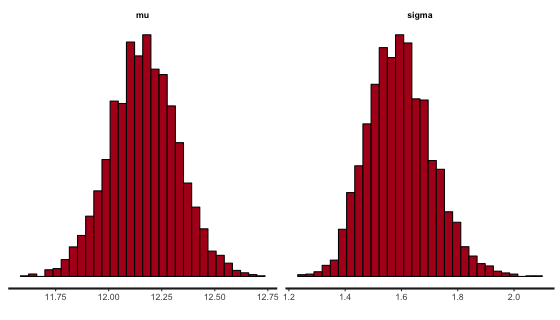

これらのプロット関数には、extract 関数と同様なオプションが用意され、特定のパラメーターのみについて図示したり、ウォームアップ区間を含まなないようにしたりすることができる。