AIC(Akaike's Information Criterion; 赤池情報量規準)は、統計モデルを評価するための指標である。ある統計モデルの最大尤度を L とし、モデルに含まれるパラメーター数を k とすると、AIC は次のように計算される。
\[ AIC = -2(logL - k) \]1 つのデータセットに対して、複数の統計モデルが考えられるとき、
観測データをモデル化しあとに、そのモデルの当てはまりの良さについて検討する必要がある。例えば、ある 1 セットの観測データがあり、左のように散布図がプロットできたとする。このデータをモデル化を行ってみる。
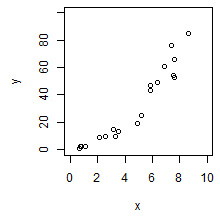
まず、1 つ目のモデルを y = ax + b とする。パラメーターとなる a および b を推定して回帰直線を書き入れると、下の左の図のようになった。次に y = ax2 + bx + c としてモデル構築し、パラメーターを推測して、二次曲線からなる近似曲線を書き入れると、下の真ん中の図のようになった。最後に、y = ax3 + bx2 + cx + d としてモデル化を行い、その近似曲線を書き入れると、下の右の図ようになった。

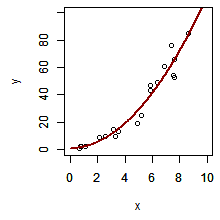
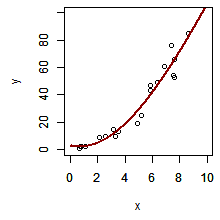
このように同じデータに対して多様なモデルを構築することができる。パラメーターの数を増やすほど、モデルの当てはまりが良くなっていく。しかし、むやみにパラメーターを増やすと、どのパラメーターが重要であるかの本質を見失う。
そこで、どのモデルが観測データを説明するのに最適なのかを評価するために、パラメーターの数やモデルの当てはまりの両方について検討を行う必要がある。例えば、2 次近似を 1 次近似に比べたとき、パラメーター数は 1 つ多いが、当てはまりの良さも非常に良くなった。一方で、3 次近似を 2 次近似を比べたとき、パラメーター数は 1 つ多いにもかかわらず当てはまりの良さがほとんど変わっていない。このような比較から 2 次近似のモデルが最適であると判定できる。(実際の検定では、当てはまりの良さやパラメーター数を計算して判定する)
上述のように 2 つのモデルが比べる方法以外に考えられる評価方法としては、まず観測データをいくつかのパラメーターでモデル構築する。次に、このモデルが最適なモデルであると仮定する。その上で、観測データをこのモデルに当てはめて、そのズレについて検討を行う。もしズレが小さければ仮定は正しく、このモデルは最適なモデルであるといえる。