補対数対数関数をリンク関数として構築した回帰モデルを補対数対数回帰回帰などとよばれている。ロジスティック回帰と同様に、一般に特徴の有無、実験動物の生死などのような 2 つの値しか取り得ない 2 値データを解析する際に適用される。このページでは、悪性黒色腫(メラノーマ)のデータセットを使用して、生存時間と悪性黒色腫に起因した生死を、補対数対数回帰を利用してモデル化する例を示す。
悪性黒色腫データ melanoma は、R の boot パッケージからを取得できる。この melanoma データには、悪性黒色腫を手術で取り除いた後の生存時間(月数)time、生存状態 status などの情報が記録されている。生存状態には 1, 2, 3 の整数が記録されている。1 は悪性黒色腫ににより死亡したことを表し、2 は調査打ち切りまで生存していたことを表し、3 は悪性黒色腫以外の原因で死亡したことを表す。ここで、モデルを構築するために、生存している場合に 1 を、悪性黒色腫により死亡した場合を 0 と表わすような変数 y を新たに作る。そして、この生存か死亡かを表わす変数 y を生存時間 x で説明する線型回帰モデルを構築する。なお、悪性黒色腫以外の原因で死亡したデータ(status が 3 のデータ)を取り除く。
※ロジスティック回帰を含む回帰モデルは、原因を用いて結果を説明するためのモデルである。このページでは、ロジスティック回帰モデルを構築するためのきれいなデータを見つけられませんでしたので、ロジスティック回帰できそうなこのデータで代用した。このデータの生存時間と悪性黒色腫の間に因果関係がなくて、本来は、このような解析を行なうべきではない。
data(melanoma, package = 'boot')
head(melanoma)
## time status sex age year thickness ulcer
## 1 10 3 1 76 1972 6.76 1
## 2 30 3 1 56 1968 0.65 0
## 3 35 2 1 41 1977 1.34 0
## 4 99 3 0 71 1968 2.90 0
## 5 185 1 1 52 1965 12.08 1
## 6 204 1 1 28 1971 4.84 1
x <- melanoma$time[melanoma$status != 3]
y <- ifelse(melanoma$status[melanoma$status != 3] == 2, 1, 0)
plot(x, y, xlab = 'time', ylab = 'alive')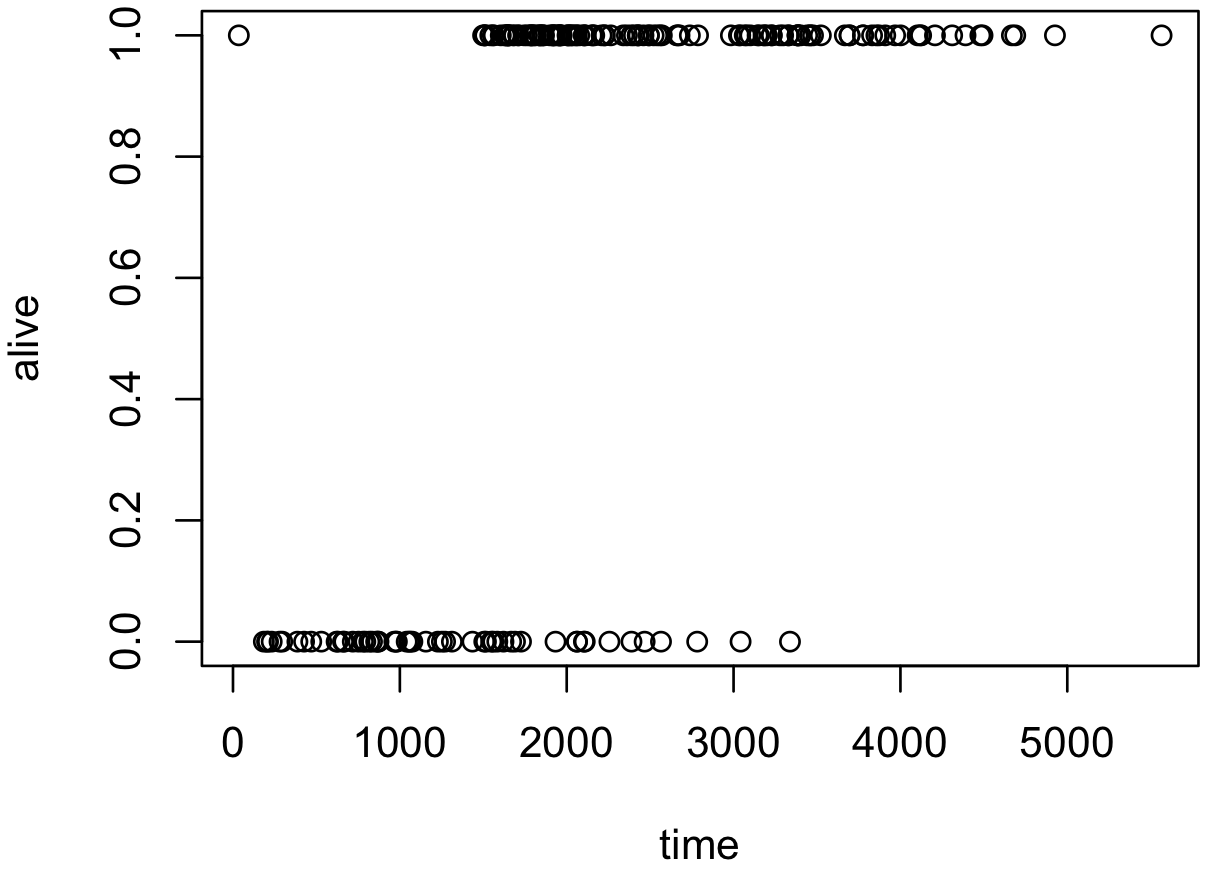
次に、プロビット回帰回帰を行うために、誤差構造を二項分布、リンク関数を補対数対数関数に指定して、glm 関数で線型回帰を行う。
model <- glm(y ~ x, family = binomial("cloglog"))
## summary(model)Call:
## glm(formula = y ~ x, family = binomial("cloglog"))
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -3.0147 -0.7318 0.1854 0.8430 1.9307
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.8156107 0.3499814 -5.188 2.13e-07 ***
## x 0.0009974 0.0001670 5.974 2.32e-09 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance: 232.84 on 190 degrees of freedom
## Residual deviance: 156.84 on 189 degrees of freedom
## AIC: 160.84
## Number of Fisher Scoring iterations: 9glm 関数の解析結果を調べると、Coefficients の項目には (Intercept) と x の行が見られる。この 2 行には、線型回帰により推定された係数が記録されている。今回の場合、生死状態 y を説明するために、生存時間 x だけを使用したので、回帰結果として生存時間にかかる係数 x と定数項 Intercept が得られる。
補対数対数回帰では、リンク関数は補対数対数関数となっている。リンク関数の各係数に上で求めた値を代入して、その逆関数を取ることで、生存率 π を計算できるようになる。
\[ \pi = 1 - \exp \left( - \exp \left( -1.8156107 + 0.0009974 \right) \right) \]この式を利用すれば実際のデータの散布図上にモデル化された曲線を描くことができる。
calc.prob <- function(xbeta) {
p <- 1 - exp(- exp(xbeta))
return(p)
}
plot(x, y, xlim = range(x), xlab = 'time', ylab = 'alive')
x.new <- seq(10, 6000, 1)
lines(x.new, calc.prob(cbind(1, x.new) %*% coef(model)))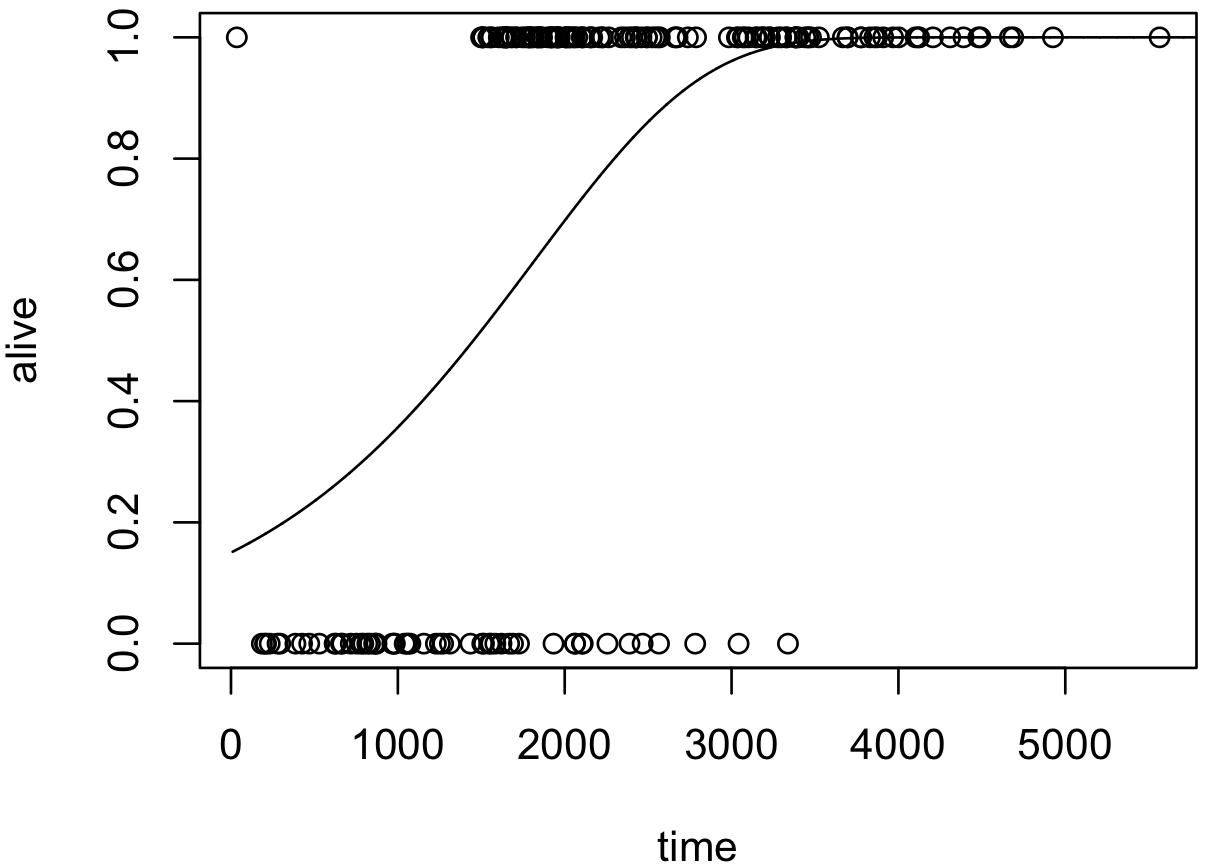
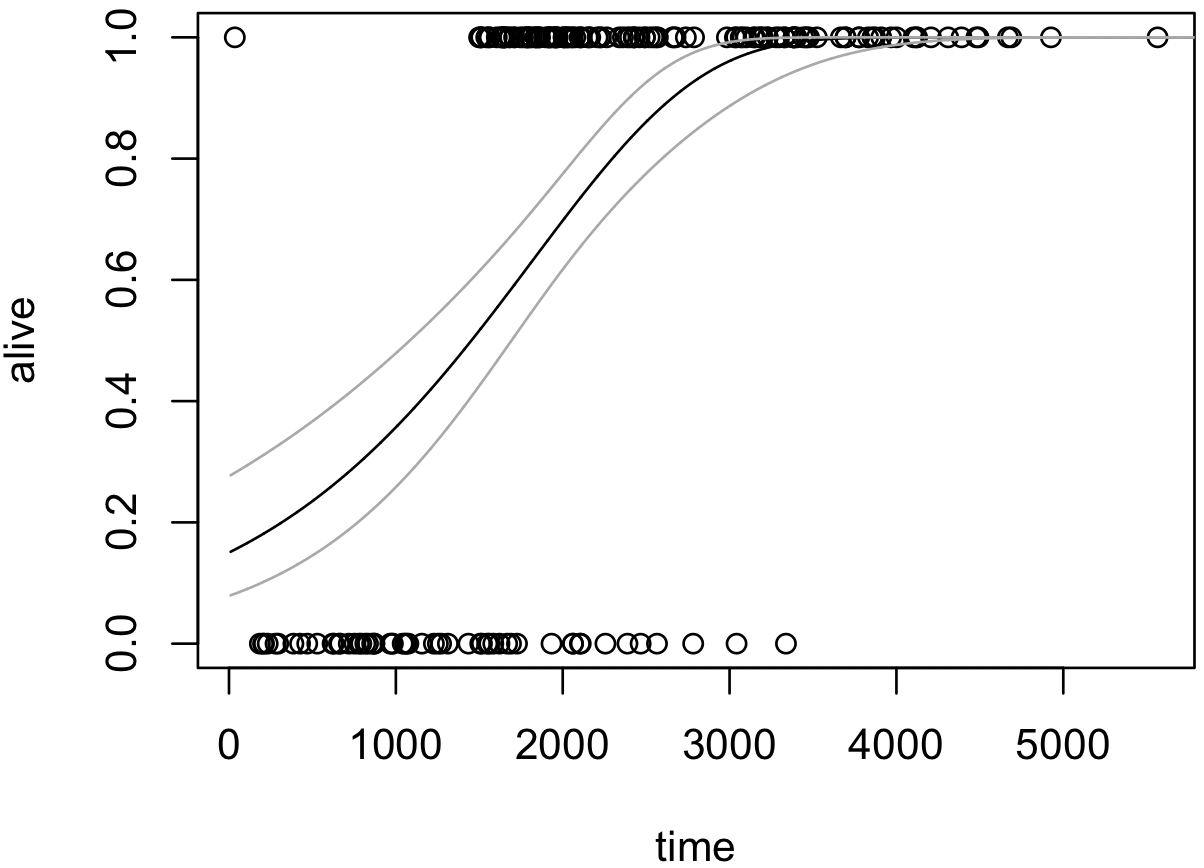
パラメーターの信頼区間について、単回帰や重回帰の場合、観測値と係数の内積 Xβ の値を計算した結果がそのまま信頼区間となる。しかし、補対数対数回帰帰を含むリンク関数が恒等関数でない一般化線型回帰モデルの場合は、自分で、線型予測子の値(Xβ)を計算し、線型予測子に対して例えば 95% 信頼区間を設けて、その上限および下限をリンク関数に代入して計算する必要がある。
線型予測子の値、すなわちリンク関数の値を計算するとき、predict 関数を使用し、オプションを type = 'link' と指定する。この関数の結果に、各 x に対応する線型予測子の期待値とその標準誤差が得られる。次に、この期待値と標準誤差を用いて 95% 信頼区間を計算する。
y.predicted <- predict(model, newdata = data.frame(x = x.new), type = 'link', se.fit = TRUE)
alpha <- 0.05
ci.lower <- y.predicted$fit - (qnorm(1 - alpha / 2) * y.predicted$se.fit)
ci.upper <- y.predicted$fit + (qnorm(1 - alpha / 2) * y.predicted$se.fit)
lines(x.new, calc.prob(ci.lower), col = 'darkgray')
lines(x.new, calc.prob(ci.upper), col = 'darkgray')