glm 関数と回帰分析 | R の glm 関数も lm 関数と同様に回帰分析を行うことができる

単回帰や重回帰は、一般化線形モデルにおいて誤差構造が正規分布で、リンク関数が恒等関数のときのことを表す。単回帰や重回帰は、基礎統計などでは lm 関数を使ってモデル構築が行われるが、一般化線形モデルを構築する際に使用する glm 関数を使用することもできる。このページでは、glm 関数を利用した回帰分析を紹介する。

単回帰分析

単回帰分析は、独立変数 X と従属変数 Y があるとき、Y を X で説明しようとする解析手法である。具体的に、2 つの変数を、Y = aX + b でモデルを立て、Y と X の関係を係数 a と b 用いて説明しようとする。ただし、従属変数 Y は正規分布に従う必要がある。

次は、sleep in mammals のデータに対して、glm 関数で単回帰分析を行う例である。sleep in mammals データは、種名（Species）、体重（BodyWt）、睡眠時間（TotalSleep）や寿命（LifeSpan）などが含むが、ここでは、寿命が睡眠時間のデータだけを使って、睡眠時間が寿命に与える影響を調べることにする。

x <- read.table("https://stats.biopapyrus.jp/data/sleep_in_mammals.txt", header = TRUE)
LifeSpan <- x$LifeSpan
TotalSleep <- x$TotalSleep

m <- glm(LifeSpan ~ TotalSleep, family = gaussian)

summary(m)
## 
## Call:
## glm(formula = LifeSpan ~ TotalSleep, family = gaussian)
## 
## Deviance Residuals:
##     Min       1Q   Median       3Q      Max
## -22.075  -10.699   -2.000    6.841   76.190
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  36.9326     5.7696   6.401 4.45e-08 ***
## TotalSleep   -1.6403     0.5057  -3.243  0.00207 **
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## 
## (Dispersion parameter for gaussian family taken to be 299.9632)
## 
##     Null deviance: 18754  on 53  degrees of freedom
## Residual deviance: 15598  on 52  degrees of freedom
##   (8 observations deleted due to missingness)
## AIC: 465.21
## 
## Number of Fisher Scoring iterations: 2

summary によって出力される各項の意味は次のようになっている。

Deviance Residuals	残差平方和の四分位数
Coefficients	予測したパラメーターの値と統計量など
Estimate	モデルパラメーターの予測値
Std. Error	標準偏差
t value	そのパラメーターが 0 かどうかの検定結果である統計量
P(>\|t\|)	t value に対応する p value
Null deviance	Null Deviance = 2(LogLikelihood(飽和モデル) - LogLikelihood(帰無モデル)) によって計算される。飽和モデルは、データの個数分だけのパラメーター（回帰係数）を用意し、構築した回帰モデルである。帰無モデルは、パラメーター（回帰係数）を 1 つだけで構築した回帰モデルである。
Residual deviance	Residual Deviance = 2(LogLikelihood(飽和モデル) - LogLikelihood(提案モデル)) によって計算される。提案モデルは、`glm` 関数に入力した回帰モデルである。上の例では、aX + b であるから、パラメーター（回帰係数）として 2 つある。
AIC	赤池情報量規準

plot(TotalSleep, LifeSpan)
abline(a = m$coefficients[1], b = m$coefficients[2])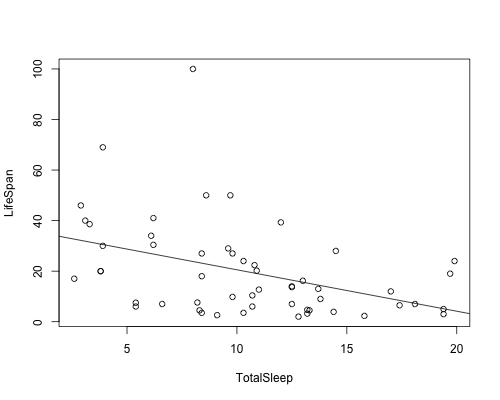

重回帰分析

glm 関数を利用した重回帰分析も、基本的に lm 関数と同じように行える。sleep in mammals のデータに対して、glm 関数で重回帰分析を行ってみる。sleep in mammals データには、種名（Species）、体重（BodyWt）、睡眠時間（TotalSleep）や寿命（LifeSpan）などが含まれている。ここで、寿命が睡眠時間と体重によって、影響されるかどうかを調べてみる。

x <- read.table("https://stats.biopapyrus.jp/data/sleep_in_mammals.html", header = TRUE)
LifeSpan <- x$LifeSpan
TotalSleep <- x$TotalSleep
BodyWt <- x$BodyWt

TotalSleep.std <- scale(TotalSleep)
BodyWt.std <- scale(BodyWt)

m <- glm(LifeSpan ~ TotalSleep.std + BodyWt.std, family = gaussian)

summary(m)
## 
## Call:
## glm(formula = LifeSpan ~ TotalSleep.std + BodyWt.std, family = gaussian)
## 
## Deviance Residuals:
##     Min       1Q   Median       3Q      Max
## -20.114  -10.484   -2.591    6.490   77.322
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)
## (Intercept)      19.630      2.333   8.415 3.28e-11 ***
## TotalSleep.std   -6.476      2.422  -2.674   0.0101 *
## BodyWt.std        3.366      2.313   1.455   0.1518
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## 
## (Dispersion parameter for gaussian family taken to be 293.6548)
## 
##     Null deviance: 18754  on 53  degrees of freedom
## Residual deviance: 14976  on 51  degrees of freedom
##   (8 observations deleted due to missingness)
## AIC: 465.01
## 
## Number of Fisher Scoring iterations: 2