1 つのデータセットに対して、2 つのモデルを作成し、2 つのモデルの応答変数の期待値に差があるかどうかを評価する方法として、検定を行う方法がある。検定は、2 つのアプローチがある。すなわち、「2 つのモデルを比較し、どのモデルが優れているかを判定する」と「構築したモデルを最適なモデルと仮定して、観測データを当てはめ、そのズレの大小でモデルが優れているかどうかを判断する」である。前者のアプローチで検定を行う方法としてWald 検定と尤度比検定がある。また、後者のアプローチで検定を行う方法としてスコア検定がある。
これらの検定手法は、2 つのモデルを想定する必要がある。一般化線形モデルによる解析において、観測データをモデル化する上で考えられるあらゆるパラメーターを使って構築したモデル(full model)と、解析者が重要と思われる少数のパラメーターのみを用いて構築したモデル(reduced model)を比較する。検定の結果として full model と reduced model がほぼ同じと判定した場合、解析者が重要と思われた少数のパラメーターが実際に重要でなかったということになる。(※目的によって full model と reduced model の作り方が異なる。ここではあくまで一例。)
full model は考えられるあらゆるパラメーターと書いたが、実際にはすべてのパラメーターを含まなくてもよい。重要な事は、reduced model を構築する際に使うパラメーターは、full model の構築する際に使うパラメーターの一部である必要がある。
つまり、考えられるあらゆるのパラメーターの集合を Θ、full model のパラメーターの集合を Θ0、reduced model のパラメーターの集合を Θ1 としたとき、各集合は以下の関係を持つ。
ここで full model のパラメーターベクトルを β0 とし、reduced model のパラメーターを β1 とすると、帰無仮説および対立仮説は以下のように表すことができる。
スコア検定
スコアは対数尤度関数の 1 次導関数として定義されている、つまり対数尤度関数の接線の傾きとなる。そこで、観測データを一般化線形モデルによりモデル化を行い、最尤法により推定されたパラメーターの最尤推定量を \(\hat{\mathbf{\beta}}\) とする。もし、現在のモデルが最適なモデルであれば、\(\hat{\mathbf{\beta}}\) における接線の傾きが限りなくゼロに近づくと考えられる。
スコア検定ではこのように、対数尤度関数の 1 次導関数(すなわち、接線の傾き)を利用した検定である。
Wald 検定
Wald 検定を利用するには full model と reduced model の 2 つのモデルを構築する必要がある。 2 つのモデルからパラメーターの最尤推定量を推定し、両者の最尤推定量の差を利用して検定を行う。
例えば、reduced model のパラメーターの最尤推定量を \(\hat{\mathbf{\beta}^{1}}\) とし、full model のパラメーターの最尤推定量を \(\hat{\mathbf{\beta}^{0}}\) とすることで、両者の差は \(\hat{\mathbf{\beta}^{1}} - \hat{\mathbf{\beta}^{0}}\) として計算できる。もし、両者の最尤推定量に差がなければ、この差がゼロに近づく。このとき、2 つのモデルは同じであるとみなせるため、reduced model に組み込んだ「重要と考えられるパラメーター」はそれほど重要でない、という判断を下すことができる。
尤度比検定
尤度比検定を利用するには full model と reduced model の 2 つのモデルを構築する必要がある。 2 つのモデルからパラメーターの最尤推定量を推定し、両者の尤度の差を利用して検定を行う。
例えば、reduced model のパラメーターの最尤推定量を \(\hat{\mathbf{\beta}^{1}}\) とし、両者の対数尤度の差は \(\log L(\hat{\mathbf{\beta}^{1}}) - \log L( \hat{\mathbf{\beta}^{1}})\) として計算できる。もし、両者の対数尤度に差がなければ、この差がゼロに近づく。このとき、2 つのモデルは同じであるとみなせるため、興味のあるモデルに組み込んだ「重要と考えられるパラメーター」はそれほど重要でない、という判断を下すことができる。
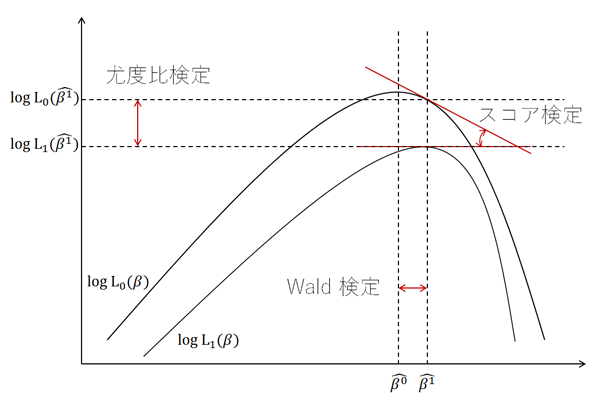
スコ検定、Wald 検定、尤度比検定の関係図
一般化線形モデルに用いられる 3 種の検定の違いを図示するとおおよそ以下のようなイメージとなる。