回帰分析で得られたモデルの適合の良さかを評価する指標として、二乗平均平方根誤差(RMSE)、平均絶対誤差(MAE)や決定係数 R2 などが用いられている。解析目的に応じて、これらを使い分ける。例えば、大きな誤差(観測値と回帰モデル出力値の差)を出すサンプルを出来るだけ少なくしたい場合は RMSE を使用するが、全サンプルの誤差を平等に評価して、サンプル全体の誤差をできるだけ小さくしたい場合は MAE を使用する。
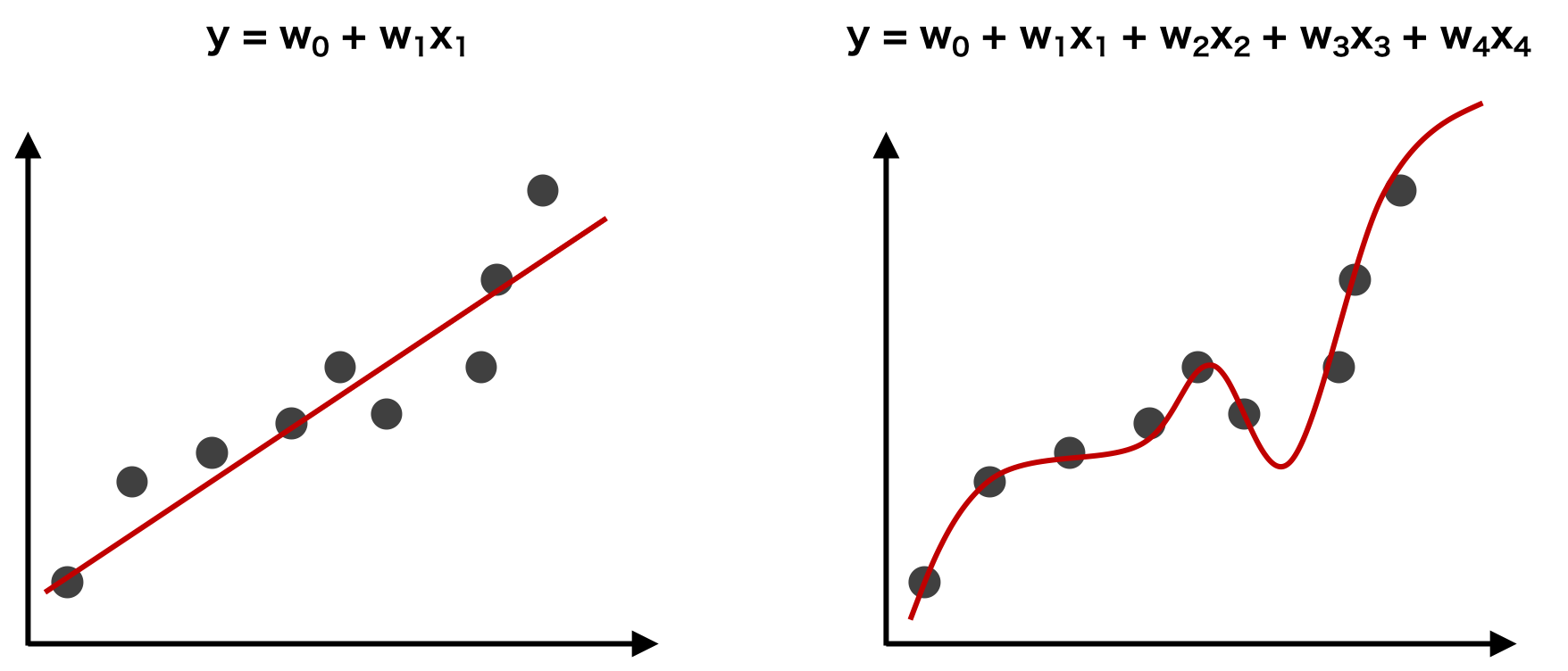
回帰モデルを評価するこれらの指標は、観測値と回帰モデルの出力値の差として計算されているため、モデルの複雑さが考慮されていない。単純なモデル(説明変数の少ないモデル)は、適合不足となり、RMSE や MAE が大きくなりがちである。一方で複雑なモデル(説明変数の多いモデル)であれば、過剰適合になり RMSE や MAE が小さくなりがちである。そのため、モデルの複雑さ適合性能の両方を評価したい場合は赤池情報量規準(AIC)などを利用する。
RMSE や MAE などの指標は、入力データに基づいて計算される。そのため、RMSE や MAE を使って二つのモデルの優劣を比較する際に、同じ入力データを使用する必要がある。例えば、アメリカのある研究室が、日本海の水温と漁獲量のデータを収集して、回帰モデル A を構築し、その RMSE が 2.3 となったとする。同様に、日本のある研究室も、まったく同じ条件で(アメリカとは独立に)データを収集して、回帰モデル J を構築し、その RMSE が 3.1 となったとする。この際に、回帰モデル A の RMSE = 2.3 が回帰モデル J の RMSE = 3.1 よりも小さいから、モデル A が優れいている、とは言えない。両者のモデルを評価するためのデータが異なっているため、その評価指標である RMSE をそのまま比較できないからである。
また、これらの指標を用いるとき、応答変数の単位にも注意する必要がある。例えば、象の重さを評価する回帰モデルにおける RMSE = 0.1 と蟻の重さを評価する回帰モデルにおける RMSE = 0.1 は同一視できない。象の重さを評価するときに 0.1g の誤差が生じても無視できるが、蟻の重さを評価するときに 0.1g の誤差が生じたときに大きな間違いとなりうる。このように、RMSE などの値のスケールは独立変数のスケールに応じて変化するため、RMSE を使ったモデル間の比較に十分に注意を支払う必要がある。
決定係数 R2
決定係数は、観測値を yi (i = 1, 2, 3, ..., n)、モデルから計算した計算値(予測値)を \(\hat{y_{i}}\)、観測値の平均を \(\bar{y}\) とすると、次の式によって定義される(他の定義方法も存在する)。観測値とモデルから計算した計算値(予測値)がほぼ同じになると、次式の分子が 0 に近づくため、R2 は 1 に近づく。逆に、観測値と予測値がかけ離れていると、分子が大きな値となり、R2 は 1 から離れた値となる。
二乗平均平方根誤差 RMSE
RMSE は、root mean squared error の略で、回帰モデルの誤差を評価する指標の一つである。RMSE は、観測値を yi (i = 1, 2, 3, ..., n)、モデルから計算した計算値(予測値)を \(\hat{y_{i}}\) とすると、次の式によって定義される。
観測値と計算値(予測値)が近づくほど、RMSE は小さくなる。逆に、観測値と計算値(予測値)が遠くなると、RMSE が著しく増える。そのため、外れ値が含まれると、観測値と計算値(予測値)の差が大きく離れるため、RMSE が著しく大きくなる。このことから、RMSE は外れ値の影響を受けやすいといわれている。
平均絶対誤差 MAE
MAE は、mean absolute error の略で、、観測値を yi (i = 1, 2, 3, ..., n)、モデルから計算した計算値(予測値)を \(\hat{y_{i}}\) とすると、次の式によって定義される。観測値と計算値(予測値)が近づくほど、MAE は小さくなる。MAE は、誤差を二乗していないので、外れ値の影響を受けにくいと言われている。
赤池情報量規準(AIC)
赤池情報量規準(Akaike's Information Criterion; AIC)は、統計モデルにおいて、モデルの複雑さ適合性能の両方を評価したい場合に用いられる。ある統計モデルの最大尤度を L とし、モデルに含まれるパラメーター数を k とすると、AIC は次のように計算される。
\[ AIC = -2(logL - k) \]