R / lm 関数による単回帰分析 | R の lm 関数で単回帰を行う方法と信頼区間・予測区間の求め方

単回帰は、1 つの独立変数で 1 つ従属変数を説明したい場合に利用される分析手法である。独立変数 x と従属変数 y を用いて、次のように数式化することができる。

\[ y = \beta_{0} + \beta_{1}x \]

単回帰のモデル式中にあるパラメーター β₀ と β₁ を求めることで、1 次関数ができる。この 1 次関数を利用することで、観測データを正しく説明できるだけでなく、予測なども行えるようになる。

lm 関数を利用した単回帰分析

ここで、trees と呼ばれているデータセットを使用して、単回帰を行う例を示す。このデータセットには 31 本の桜の木の周長（Grith）、高さ（Height）、および容積（Volume）のデータが記録されている。樹木が高くなるには、それを支えるために幹も太くなる必要がある。そのため、幹が太さを使って木の高さを説明できる可能性がある。そこで、この仮定をもとに、Grith を独立変数とし、Height を従属変数として、単回帰を行う。

data(trees)
head(trees)
##   Girth Height Volume
## 1   8.3     70   10.3
## 2   8.6     65   10.3
## 3   8.8     63   10.2
## 4  10.5     72   16.4
## 5  10.7     81   18.8
## 6  10.8     83   19.7

plot(x, y, xlab = 'Girth', ylab = 'Height')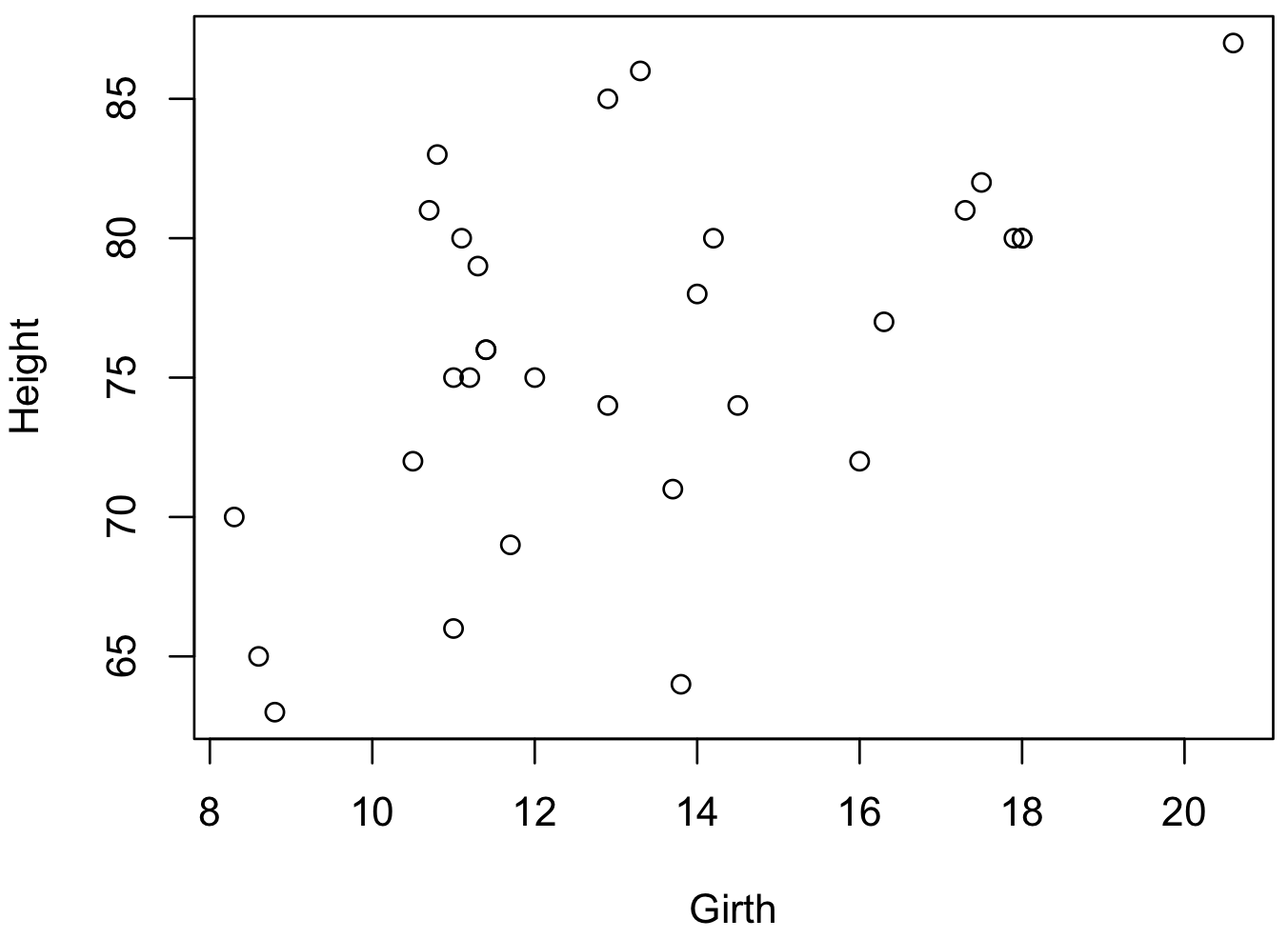

上の図から、独立変数 x の値の大きさに関わらず、従属変数 y のばらつきはほぼ一定であることが確認できる。そこで、従属変数 y が正規分布に従うと仮定して、回帰モデルを作成する。このサンプルデータを lm 関数に代入し、回帰モデルを作成する。

y <- trees$Height
x <- trees$Girth

m <- lm(y ~ x)

summary(m)Call:
## lm(formula = y ~ x)
## Residuals:
##      Min       1Q   Median       3Q      Max
## -12.5816  -2.7686   0.3163   2.4728   9.9456
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)
## (Intercept)  62.0313     4.3833  14.152 1.49e-14 ***
## x             1.0544     0.3222   3.272  0.00276 **
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## Residual standard error: 5.538 on 29 degrees of freedom
## Multiple R-squared:  0.2697,	Adjusted R-squared:  0.2445
## F-statistic: 10.71 on 1 and 29 DF,  p-value: 0.002758

 coef(m)
## (Intercept)           x
##   62.031314    1.054369

回帰モデルに含まれているパラメーター β₀ と β₁ は、Coefficients の内容をみると、それぞれ 62.031314 および 1.054369 となっていることがわかる。つまり、この解析結果から、回帰直線 y = 1.054369x + 62.031314 が求められた。また、Coefficients 項目の Pr(>|t|) の列は、各パラメーターがゼロかどうかを検定した結果を p 値で示したものである。例えば、β₁ は Pr(>|t|) = 0.00276 となっているため、有意水準 5% のもとで、この回帰モデルの係数 β₁ はゼロでないことを表している。つまり、x (Girth) は、何らかのしくみで y (Height) に関与していると説明できる。

回帰直線を描くとき、abline 関数などを使用すると便利である。

plot(x, y, xlab = 'Girth', ylab = 'Height')
abline(m)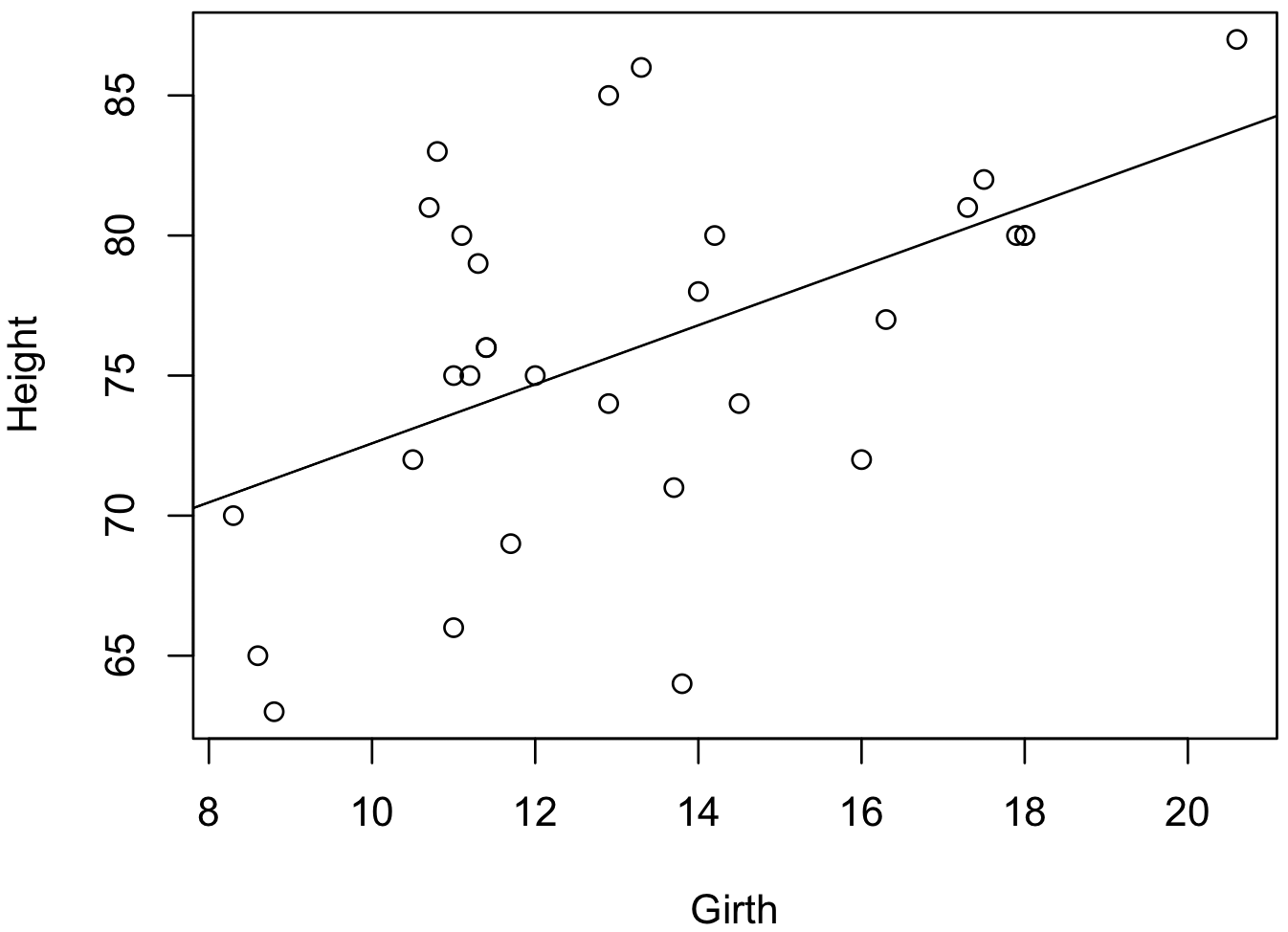

信頼区間と予測区間

回帰分析で得られる回帰モデルに対して、信頼区間と予測区間を求めることができる。信頼区間は、母平均がある確率で入る区間のことをさす。これに対して、予測区間は、今後、新たに標本（データ）を取得するとき、その標本がある確率で入る区間のことをさす。

信頼区間

単回帰で計算された回帰直線から、信頼区間を取得するのに predict 関数を利用する。このとき、引数 interval = 'confidence' を指定する。デフォルトでは 95% 信頼区間が計算されるが、信頼区間の範囲を変更する場合は level 引数を調整する。信頼区間の計算結果は、3 列からなり、fit 列は x を回帰直線に代入して得られる値であり、lwr は信頼区間の下限で、upr は信頼区間の上限である。

newx <- data.frame(x = seq(8, 22, 0.2))
conf.interval <- predict(m, newdata = newx, interval = 'confidence', level = 0.95)
head(conf.interval)
##        fit      lwr      upr
## 1 70.46626 66.45349 74.47903
## 2 70.67714 66.77740 74.57687
## 3 70.88801 67.10010 74.67592
## 4 71.09889 67.42147 74.77630
## 5 71.30976 67.74140 74.87812
## 6 71.52063 68.05974 74.98153

plot(x, y, xlab = 'Girth', ylab = 'Height')
abline(m)

lines(newx$x, conf.interval[, 1], col = 'orange')
lines(newx$x, conf.interval[, 2], col = 'darkgreen')
lines(newx$x, conf.interval[, 3], col = 'darkgreen')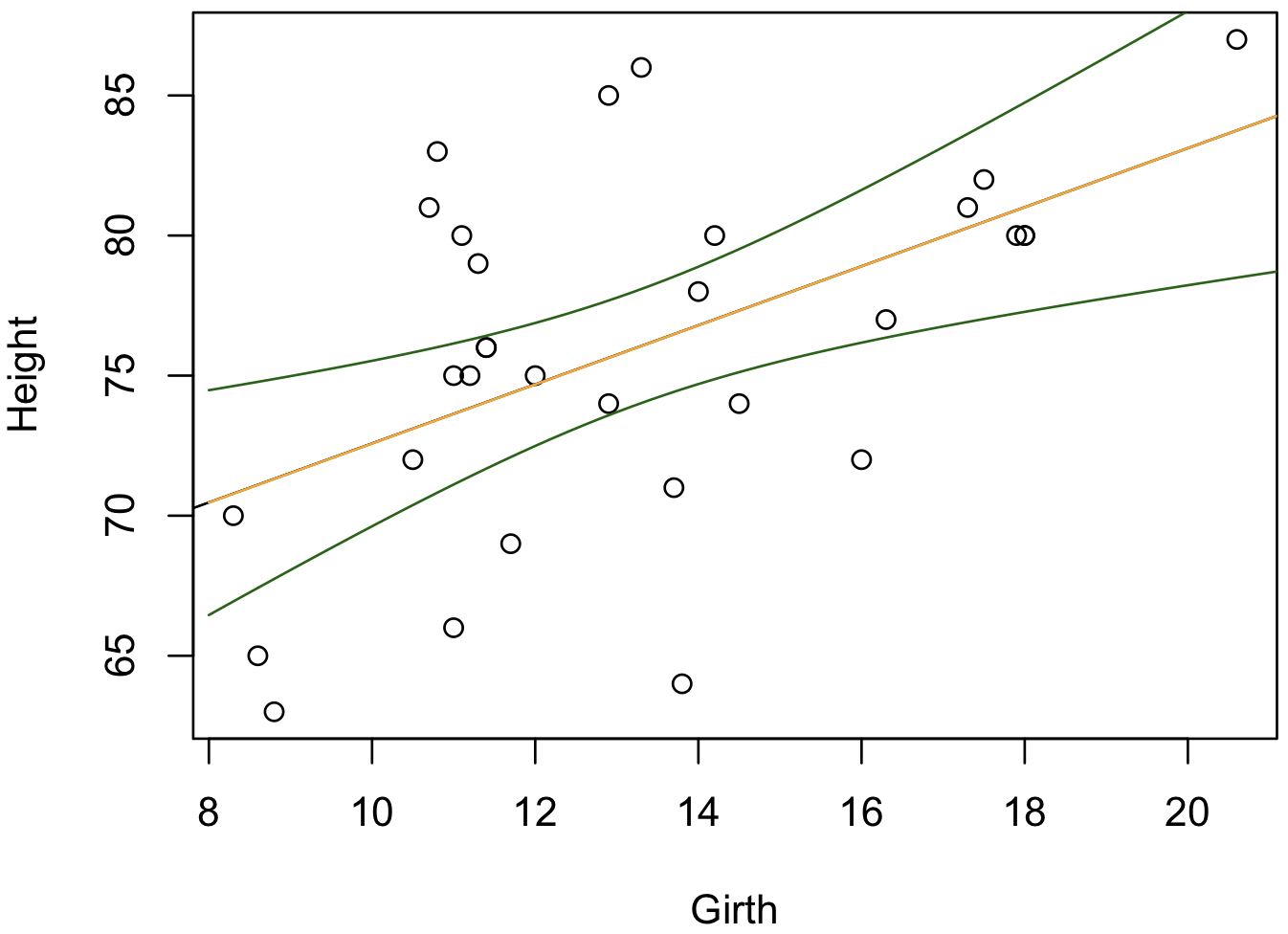

予測区間

予測区間は、 predict 関数を利用して、引数 interval = 'prediction' を指定する。信頼区間の計算結果は、3 列からなり、fit 列は x を回帰直線に代入して得られる値であり、lwr は信頼区間の下限で、upr は信頼区間の上限である。

newx <- data.frame(x = seq(8, 22, 0.2))
pred.interval <- predict(m, newdata = newx, interval = 'prediction', level = 0.95)
head(pred.interval)
##        fit      lwr      upr
## 1 70.46626 58.44906 82.48347
## 2 70.67714 58.69721 82.65707
## 3 70.88801 58.94401 82.83201
## 4 71.09889 59.18947 83.00830
## 5 71.30976 59.43356 83.18596
## 6 71.52063 59.67628 83.36498


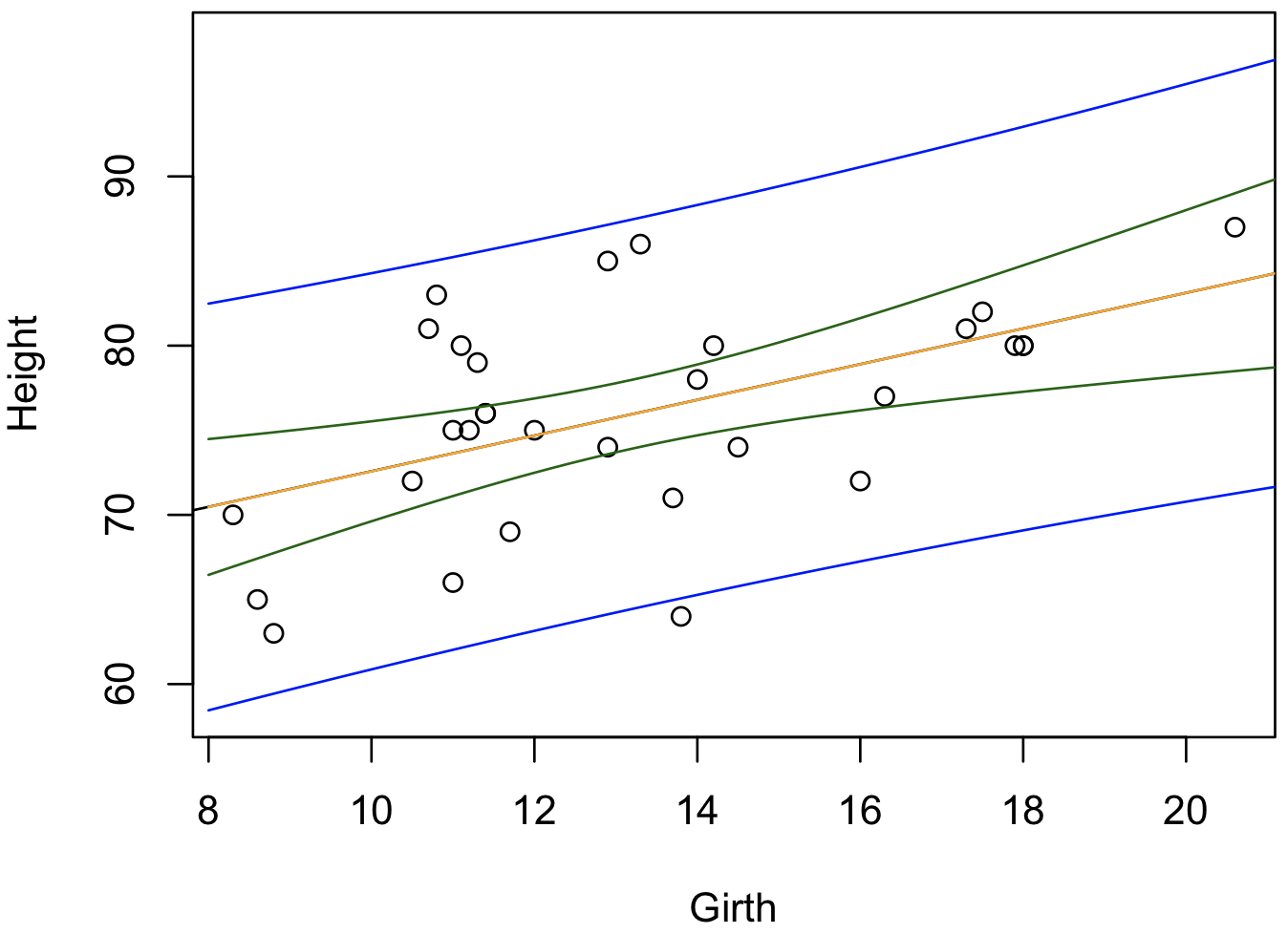
plot(x, y, xlab = 'Girth', ylab = 'Height', ylim = range(pred.interval))
abline(m)

lines(newx$x, conf.interval[, 1], col = 'orange')
lines(newx$x, conf.interval[, 2], col = 'darkgreen')
lines(newx$x, conf.interval[, 3], col = 'darkgreen')
lines(newx$x, pred.interval[, 2], col = 'blue')
lines(newx$x, pred.interval[, 3], col = 'blue')