IRLS で解く最尤推定量 | ニュートン・ラフソン法を利用して一般化線形モデルのパラメーターを推定する方法

一般化線形モデルの対数尤度関数から最尤推定量を計算する際に \(\frac{\partial l(\beta)}{\partial \beta}=0\) の解を求める必要がある。この方程式をニュートン・ラフソン法により求めることができる。

ニュートン・ラフソン法

関数 y = f(x) があり f(x)= 0 となる解を近似法によって求めるのがニュートン・ラフソン法である。

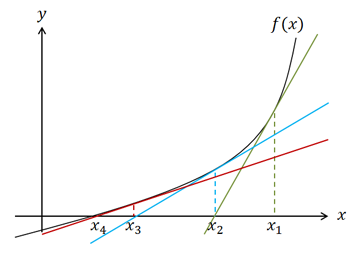
f(x) = 0 の解を求めるために、グラフ上の任意の点 x = x₁ における接線（緑色）を計算する。次に、x = x₁ における接線と x 軸の交点を x² として、x = x₂ における接線（青色）を計算する。さらに、次に、x = x₂ における接線と x 軸の交点を x₃ として、x = x₃ における接線（赤色）を計算する。このように x₄、x₅ …と繰り返して求めていけば、x_n が限りなく f(x) = 0 の解に近づく。このようなアルゴリズムを用いた方程式の解法をニュートン・ラフソン法という。

x_m から x_m+1 を求めるとき、以下のように数式化することができる。

\[ 0 - f(x_{m}) = f'(x_{m})(x_{m+1} - x_{m}) \] \[ \therefore 0 = f(x_{m}) + f'(x_{m})(x_{m+1} - x_{m}) \]

ニュートン・ラフソン法（IRLS）による最尤推定量の求め方

ニュートン・ラフソン法を応用するために、上で説明した関数 f を \( \frac{\partial l(\beta)}{\partial \beta} \) とみなせばよい。(m+1) 回目のパラメータ β^(m+1) を計算する際に以下のように計算する。

\[ 0 = \left . \frac{\partial l}{\partial \beta} \right \vert_{(m)} + \left . \frac{\partial ^{2} l}{\partial \beta \partial \beta^{T}} \right \vert_{(m)} (\beta^{(m+1)}-\beta^{(m)}) \] \[ \therefore \beta^{(m+1)} = \beta^{(m)} - \frac{\left . \frac{\partial l}{\partial \beta} \right \vert_{(m)}}{\left . \frac{\partial ^{2} l}{\partial \beta \partial \beta^{T}}\right \vert_{(m)} } \]

2 階微分の計算が難しいため、その期待値を利用する。すなわち、\( \frac{\partial ^{2} l}{\partial \beta \partial \beta^{T}} \) の代わりに \( E\left[ \frac{\partial ^{2} l}{\partial \beta \partial \beta^{T}} \right]\) を用いる。

このように対数尤度関数の 2 階微分の期待値を利用した方法は、反復重み付け最小二乗法（IRLS）とも呼ばれている。

\[ \begin{eqnarray} \beta^{(m+1)} &=& \beta^{(m)} - \frac{\left . \frac{\partial l}{\partial \beta} \right \vert_{(m)}}{\left .E\left[ \frac{\partial ^{2} l}{\partial \beta \partial \beta^{T}} \right]\right \vert_{(m)} } \\ &=& \beta^{(m)} + \frac{\left . \frac{\partial l}{\partial \beta} \right \vert_{(m)}}{\left . - E\left[ \frac{\partial ^{2} l}{\partial \beta \partial \beta^{T}} \right]\right \vert_{(m)} } \\ &=& \beta^{(m)} + \frac{\mathbf{U}^{m}}{\mathbf{I}^{(m)}} \\ &=& \beta^{(m)} + \left [ \mathbf{I}^{(m)} \right ] ^{-1} \mathbf{U}^{m} \\ &=& \beta^{(m)} + \left [ \mathbf{X}^{T}\mathbf{W}\mathbf{X}^{(m)} \right ] ^{-1} \mathbf{U}^{m} \\ \end{eqnarray} \]

この式を利用して、ニュートン・ラフソン法により、\( l(\beta^{(n+1)}) - l(\beta^{(n)}) \lt \delta \) になるまで繰り返す（\(\delta \rightarrow 0\)）。しかし、観測されたデータの分布に偏りがある場合は、計算が収束しない場合がある。例えば、ゼロ過剰の二項分布などがそうである。

R を利用したニュートン・ラフソン法の実装

以下のサンプルデータを利用して、ポアソン回帰を行い、そのパラメーターをニュートン・ラフソン法により推測する。

サンプルデータはポアソン分布に従うように乱数生成したものである。ある実験区画に入り込むある絶滅危惧種の個体数を計数したデータである。計数は 1 年間 4 回行い、これを 5 年間続けた。このデータを利用して、年が経つ毎に個体数がどのように増えたのかをポアソン回帰によりモデル化する。

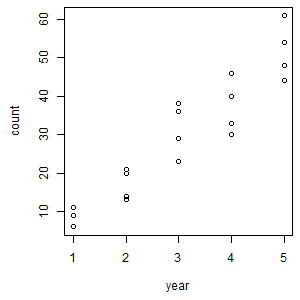
計数    1回目 2回目 3回目 4回目
1 年目    6     9    11    11
2 年目    21   14    13    20
3 年目    38   36    23    29
4 年目    30   33    46    40
5 年目    64   48    54    44

右図は、横軸を経過年数、縦軸を観測値としてプロットした散布図である。観測値が小さい時、そのばらつきも小さい。逆に、観測値が大きくなると、そのばらつきも大きくなっていることが確認できる。

ポアソン回帰を行うとき、リンク関数（g）およびパラメーター（β₁、β₂）を以下のように設定する。

\[ g(\lambda) = \log\lambda = \beta_{1} + \beta_{2} \cdot year \]

観測値ベクトル y 、パラメーターベクトル β およびデザイン行列 X は以下のように書ける。

\[ \mathbf{y} = \begin{pmatrix} 6 \\ 9 \\ 11 \\ 11 \\ 21 \\ \vdots \\ 47 \end{pmatrix}, \mathbf{X} = \begin{pmatrix} 1 & 1 \\ 1 & 1 \\ 1 & 1 \\ 1 & 1 \\ 1 & 2 \\ \vdots & \vdots \\ 1 & 5 \end{pmatrix}, \mathbf{\beta} = \begin{pmatrix} \beta_{1} \\ \beta_{2} \end{pmatrix} \]

ニュートン・ラフソン法を利用する際に上で挙げた観測値ベクトル、デザイン行列、パラメーターベクトルのほかに W や U なども必要とする。

\[ \begin{eqnarray} \mathbf{U} &=& \sum _{i=1}^{n} \frac{(y_{i} - \mu_{i})\mathbf{x}^{T}_{i \cdot}}{g'(\lambda_{i})Var[y_{i}]} \\ &=& \sum _{i=1}^{n} (y_{i} - \mu_{i})\mathbf{x}^{T}_{i \cdot} \\ \mathbf{W} &=& \begin{pmatrix} \frac{1}{(g'(\mu_{1}))^{2} Var[y_{1}]} & 0 & \cdots & 0 \\ 0 & \frac{1}{(g'(\mu_{2}))^{2} Var[y_{2}]} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \frac{1}{(g'(\mu_{n}))^{2} Var[y_{n}]} \\ \end{pmatrix} \\ &=& \begin{pmatrix} \lambda_{1} & 0 & \cdots & 0 \\ 0 & \lambda_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_{n} \\ \end{pmatrix} \end{eqnarray} \]

行列の準備はこれで終わり。次に観測値、デザイン行列およびパラメーターを R の変数に保存する。

Y <- c( 6,  9, 11, 11,
       21, 14, 13, 20,
       38, 36, 23, 29,
       30, 33, 46, 40,
       61, 48, 54, 44)
X <- cbind(
       rep(1, length(Y)),
       c(1, 1, 1, 1,
         2, 2, 2, 2,
         3, 3, 3, 3,
         4, 4, 4, 4, 
         5, 5, 5, 5))

次に、for 文を利用して 99 回ニュートン・ラフソン法を繰り返して実行する。パラメーターの初期値はそれぞれ 1 と 10 に設定する。全 100 セットのパラメーターは行列型の beta 変数に保存される。

beta <- matrix(0, ncol = 2, nrow = 100)
beta[1, ] <- c(1, 10)
for (m in 2:100) {
  lambda <- exp(X %*% beta[m - 1, ])
  W <- diag(lambda[, 1])
  XtWX <- t(X) %*% W %*% X
  U <- t(Y - lambda) %*% X
  beta[m, ] <- beta[m - 1, ] + solve(XtWX) %*% t(U)
}

推定されたパラメーターをプロットすると、約 50 回繰り返したあとに、パラメーターが収束したと確認できる。

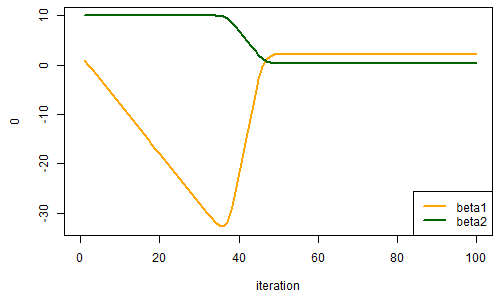
具体的にはパラメーターは以下の値に収束した。

tail(beta)
##           [,1]      [,2]
## [95,]  2.09693 0.3806021
## [96,]  2.09693 0.3806021
## [97,]  2.09693 0.3806021
## [98,]  2.09693 0.3806021
## [99,]  2.09693 0.3806021
## [100,] 2.09693 0.3806021

次に、同じことを R の glm 関数で行うと、結果は以下のようになる。(Intercept) の予測値が 2.09693、X2 の予測値が 0.38060 となり、上で求めた値と同じになったことが確認できる。

poi.model <- glm(Y ~ X, family = poisson(link = "log"))
summary(poi.model)
## Call:
## glm(formula = Y ~ X, family = poisson(link = "log"))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.8959  -0.8895  -0.2677   0.7155   2.3056  
## 
## Coefficients: (1 not defined because of singularities)
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  2.09693    0.12565   16.69   <2e-16 ***
## X1                NA         NA      NA       NA    
## X2           0.38060    0.03193   11.92   <2e-16 ***
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 180.724  on 19  degrees of freedom
## Residual deviance:  25.271  on 18  degrees of freedom
## AIC: 130.12
## 
## Number of Fisher Scoring iterations: 4

References

P.M.E.Altham, Statistical Laboratory, University of Cambridge. Introduction to Generalized Linear Modelling. 2011. PDF
Dobson AJ. An Introduction to Generalized Linear Models. Second Edition. 2002.
ニュートン法. Wikipedia