回帰分析は多変量解析法の一つである。1 つの従属変数 y を、複数の独立変数 xi (i = 1, 2, ..., n) でモデル化し、それらの関係や傾向を分析する方法である。そのモデル式は、次のように書くことができる。
\[ y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \cdots + \beta_{n}x_{n} \]データセットの準備
R の lm を利用して、重回帰分析を行なってみる。ここではサンプルデータとして、哺乳類の睡眠時間を調査したデータを利用する。このデータには、動物の名前(Species)、体重(BodyWt)、睡眠時間(TotalSleep)、寿命(LifeSpan)などが記載されている。ここでは、寿命を従属変数として、体重と睡眠時間を独立変数として、重回帰分析を行う。その結果をもとに、寿命は、体重あるいは睡眠時間のどちらかに強く影響されるかを考えてみる。
x <- read.table("https://stats.biopapyrus.jp/data/sleep_in_mammals.txt", header = TRUE)
head(x)
## Species BodyWt BrainWt NonDreaming Dreaming TotalSleep LifeSpan Gestation Predation Exposure Danger
## 1 Africanelephant 6654.000 5712.0 NA NA 3.3 38.6 645 3 5 3
## 2 Africangiantpouchedrat 1.000 6.6 6.3 2.0 8.3 4.5 42 3 1 3
## 3 ArcticFox 3.385 44.5 NA NA 12.5 14.0 60 1 1 1
## 4 Arcticgroundsquirrel 0.920 5.7 NA NA 16.5 NA 25 5 2 3
## 5 Asianelephant 2547.000 4603.0 2.1 1.8 3.9 69.0 624 3 5 4
## 6 Baboon 10.550 179.5 9.1 0.7 9.8 27.0 180 4 4 4まず、データセット全体から必要な LifeSpan, BodyWt, および TotalSleep だけを取し、欠損地を削除し、分布を確認する。
LifeSpan <- x$LifeSpan
BodyWt <- x$BodyWt
TotalSleep <- x$TotalSleep
isna <- is.na(LifeSpan) | is.na(BodyWt) | is.na(TotalSleep)
LifeSpan <- LifeSpan[!isna]
BodyWt <- BodyWt[!isna]
TotalSleep <- TotalSleep[!isna]
par(mfrow = c(1, 3))
hist(LifeSpan)
hist(BodyWt)
hist(TotalSleep)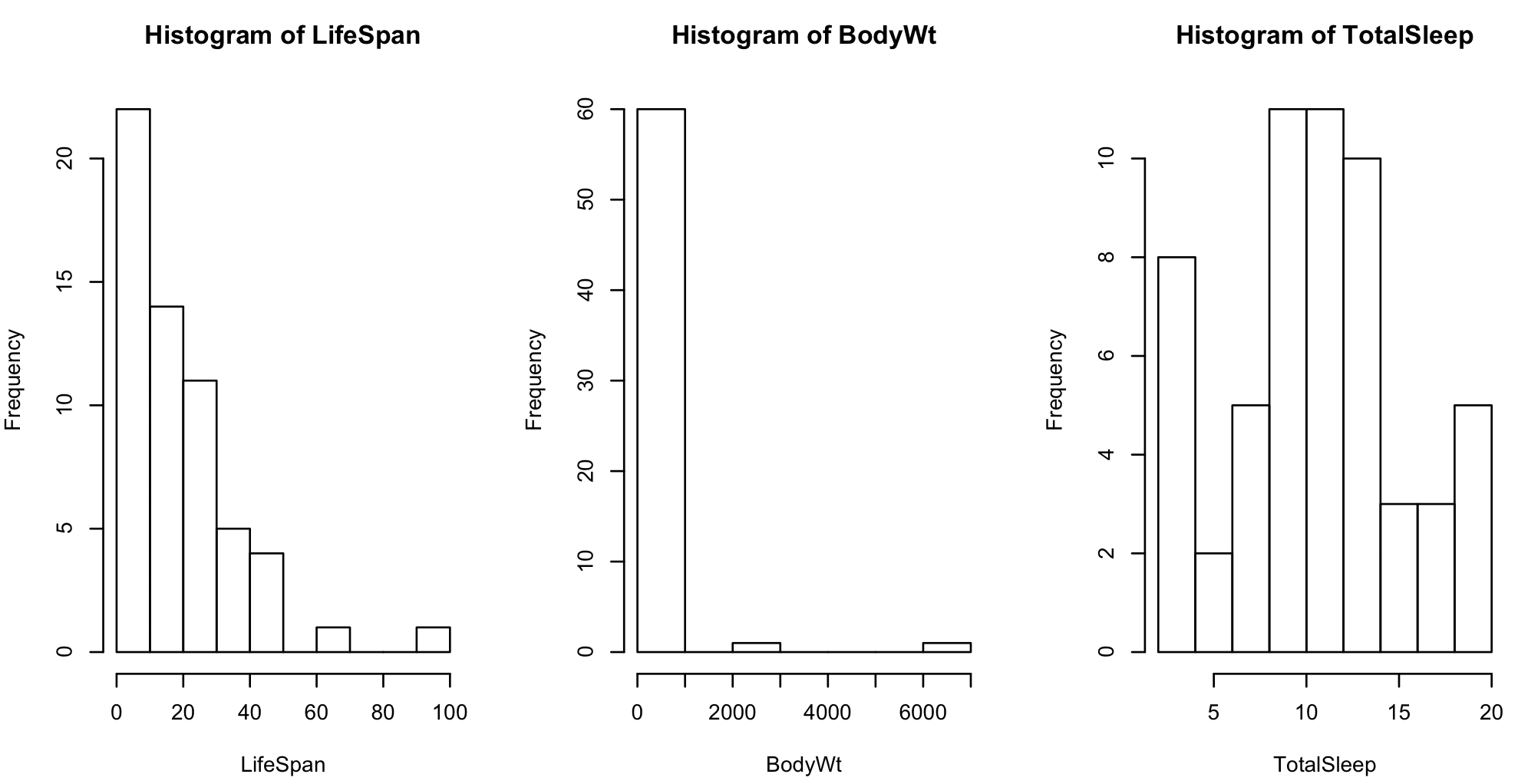
データの分布を確認すると、LifeSpan と BodyWt が、正規分布から著しく離れていることがわかる。回帰分析は、基本的にデータが正規分布に従う場合のみに利用できる。そこで、ここで対数変換を行なって、LifeSpan と BodyWt を正規分布に近づけてみる。(※ 対数変換を行わずに、GLM を利用して解析した方がいいかも。)
LifeSpan.log <- log10(LifeSpan)
BodyWt.log <- log10(BodyWt)
par(mfrow = c(1, 3))
hist(LifeSpan.log)
hist(BodyWt.log)
hist(TotalSleep)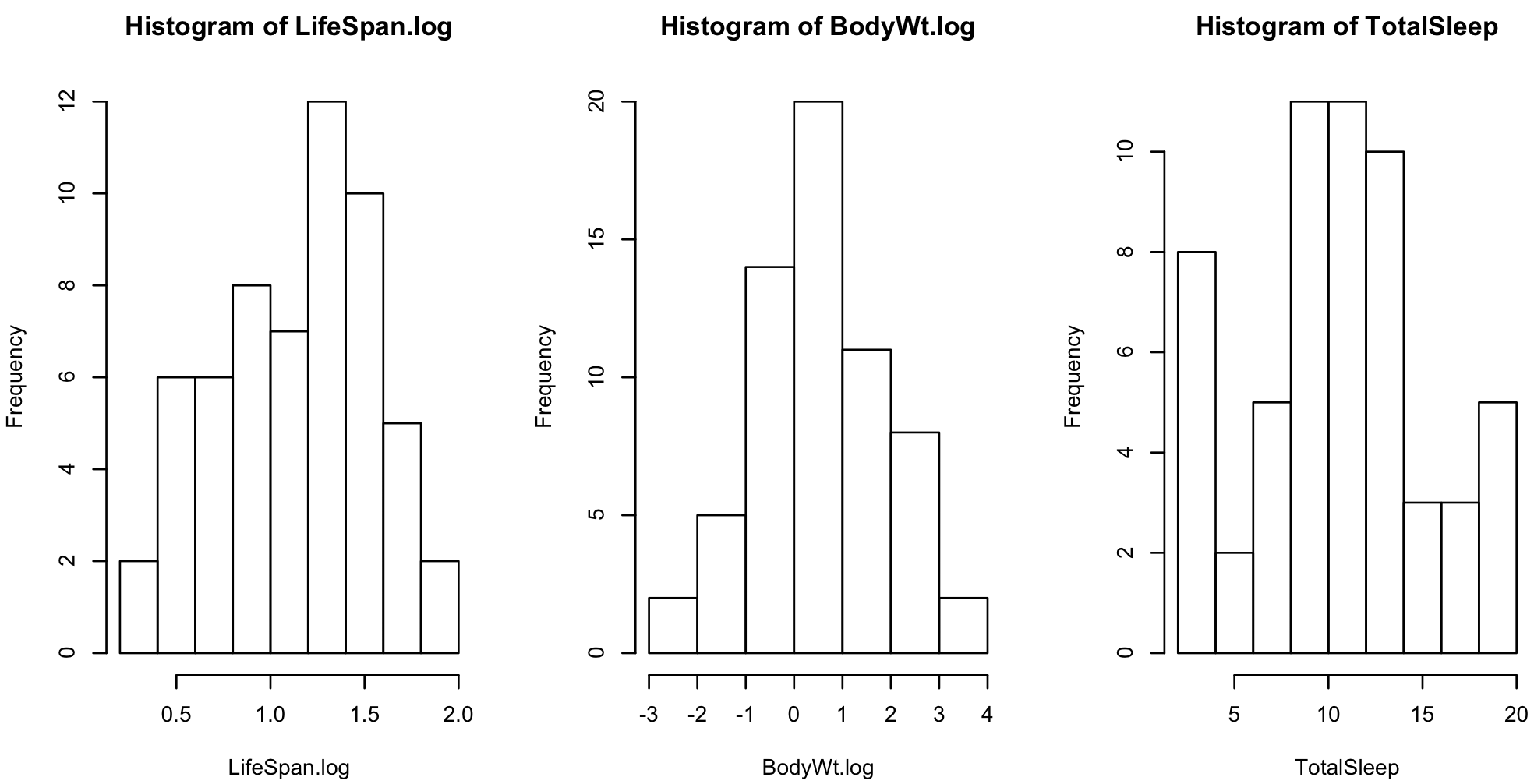
LifeSpan と BodyWt のデータ分布がだいぶ正規分布に近づいた。ここで、回帰分析を行なってみる。独立変数である体重と睡眠時間は、単位が異なるので、解析する前に両者が同じ比重となるように標準化する。
BodyWt.log.std <- scale(BodyWt.log)
TotalSleep.std <- scale(TotalSleep)回帰モデルの構築
データセットの準備と標準化が終わりに、次に重回帰モデルを作成する。
\[ LifeSpan = \beta_{0} + \beta_{1}BodyWt + \beta_{2}TotalSleep \]m <- lm(LifeSpan.log ~ TotalSleep.std + BodyWt.log.std)
summary(m)
##
## Call:
## lm(formula = LifeSpan.log ~ TotalSleep.std + BodyWt.log.std)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.57995 -0.19894 -0.05503 0.16127 0.84891
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.11941 0.04121 27.167 < 2e-16 ***
## TotalSleep.std -0.02846 0.04829 -0.589 0.558
## BodyWt.log.std 0.27866 0.04873 5.718 5.65e-07 ***
## ---
## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
##
## Residual standard error: 0.3024 on 51 degrees of freedom
## (8 observations deleted due to missingness)
## Multiple R-squared: 0.5033, Adjusted R-squared: 0.4838
## F-statistic: 25.84 on 2 and 51 DF, p-value: 1.781e-08Cofficients 項の Estimate 列に、回帰モデルの係数が書かれている。この場合、この回帰モデルは、LifeSpan = -0.02846×TotalSleep + 0.27866×BodyWt + 1.11941 となる。この解析結果から、体重が増えるほど寿命が長くなり、睡眠時間が長いほど寿命が短くなる傾向がみられる。また、睡眠時間よりも、体重が寿命に与える影響が強いと読み取ることができる。
回帰モデルの評価
睡眠時間が寿命に与える影響は比較的に弱いことがわかった。そこで、体重と睡眠時間を使ったモデル(m1)と体重のみを使ったモデル(m2)を作成し、両者の適合の良さを比較してみる。両者の RMSE を比較すると、m1 モデルの方の RMSE がわずかに小さい。しかし、AIC を比較すると、明らかに m2 モデルの方が優れていることがわかる。以上のことから、睡眠時間と体重の両方を使って寿命を説明するモデルよりも、体重だけを使って寿命を説明するモデルの方が優れていると言える。独立変数が多いとき、すべての独立変数をモデルに組み込むことが、必ずしもよいことではないことがわかる。
m1 <- lm(LifeSpan.log ~ TotalSleep.std + BodyWt.log.std)
sqrt(sum(resid(m1)^2)/length(resid(m1)))
## [1] 0.2939153
AIC(m1)
## [1] 29.00329
m2 <- lm(LifeSpan.log ~ BodyWt.log.std)
sqrt(sum(resid(m2)^2)/length(resid(m2)))
## [1] 0.2949143
AIC(m2)
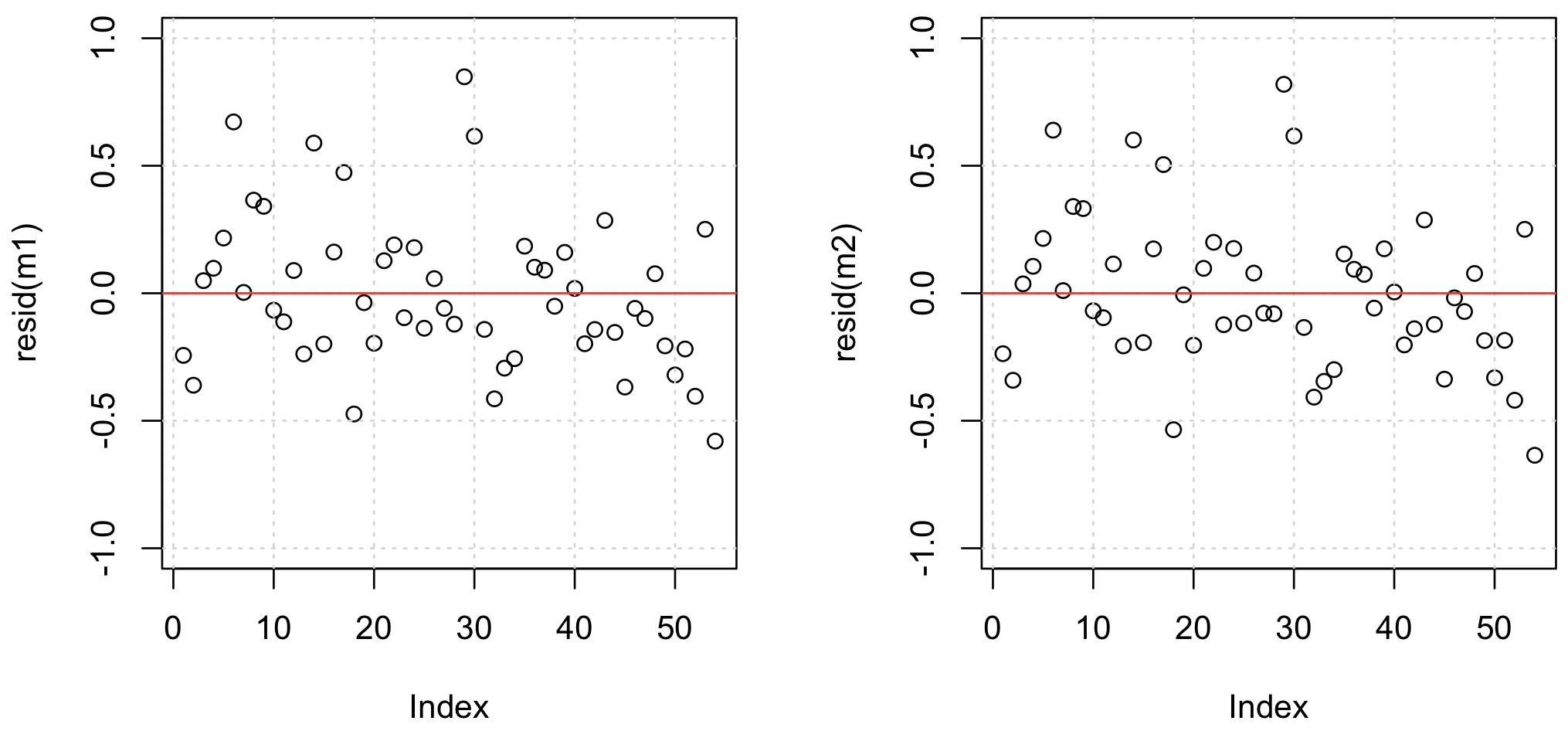
## [1] 27.36976両方のモデルの残差プロットを描き、視覚的に見比べてみる。
par(mfrow = c(1, 2))
plot(resid(m1), ylim = c(-1, 1))
grid()
abline(h = 0, col = 'red')
plot(resid(m2), ylim = c(-1, 1))
grid()
abline(h = 0, col = 'red')