ポアソン回帰はカウントデータあるいはイベントの発生率をモデル化する際に用いられる。このページでは、島の面積とその島で生息している動物の種数を、ポアソン回帰でモデル化する例を示す。このデータセットは R の faraway パッケージに保存されている。また、このデータセットには、島の面積と種数以外のデータも記録されているが、ここでは使用しない。

data(gala, package = 'faraway')
head(gala)
##              Species Endemics  Area Elevation Nearest Scruz Adjacent
## Baltra            58       23 25.09       346     0.6   0.6     1.84
## Bartolome         31       21  1.24       109     0.6  26.3   572.33
## Caldwell           3        3  0.21       114     2.8  58.7     0.78
## Champion          25        9  0.10        46     1.9  47.4     0.18
## Coamano            2        1  0.05        77     1.9   1.9   903.82
## Daphne.Major      18       11  0.34       119     8.0   8.0     1.84

plot(log10(gala$Area), gala$Species, xlab = 'log10(Area)', ylab = 'Species')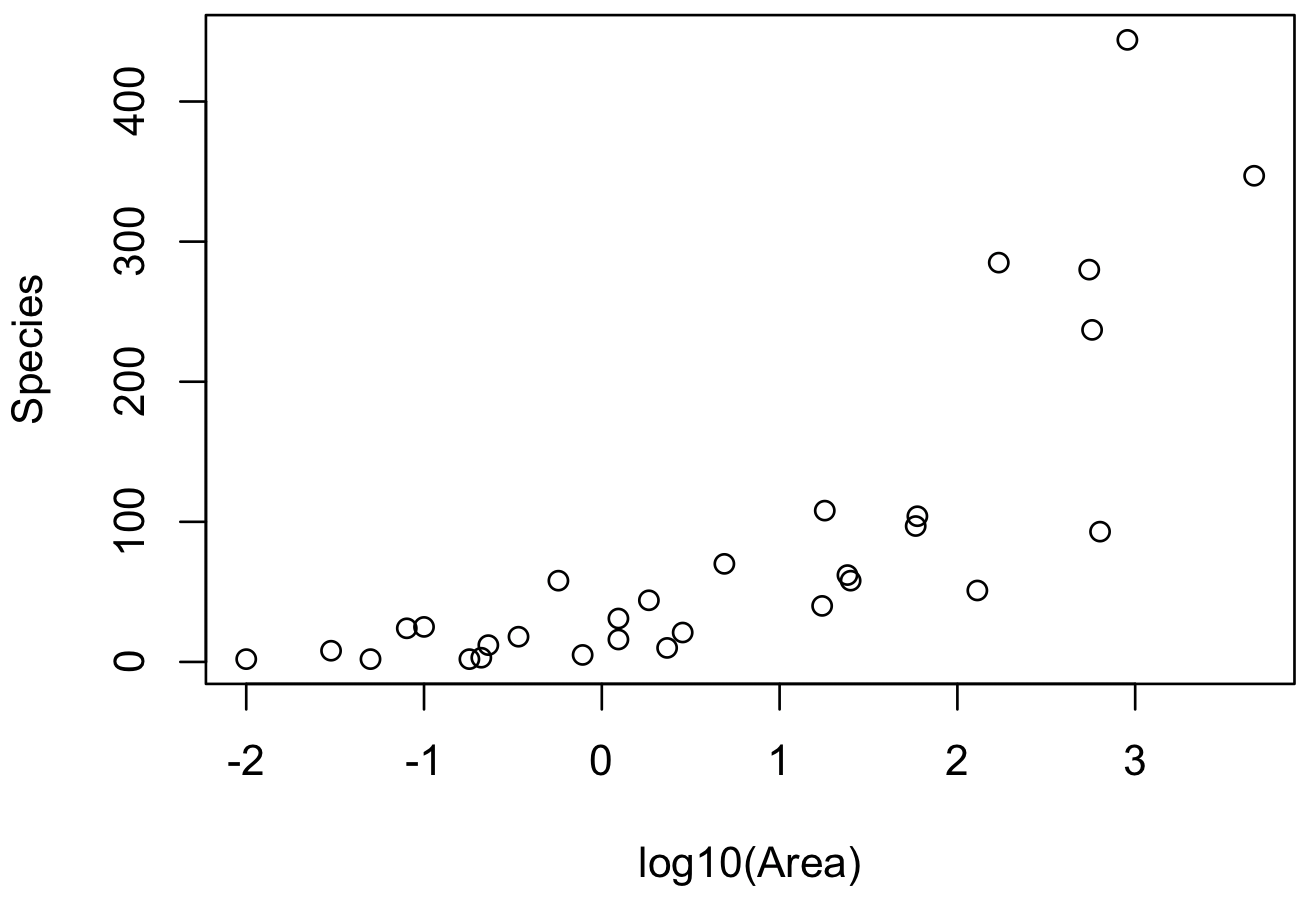

モデル化

誤差構造をポアソン分布とした時、期待値と分散はそれぞれ次のように求められる。

また、デザイン行列を X、パラメーターを β、リンク関数を g とすると、モデルは以下のように構築される。

ここで、感染者数（Y）はカウントデータであるため、マイナスの値を取ることはない。しかし、デザイン行列の値次第で上式の右辺はマイナスとなることもある。そのため、リンク関数の逆関数を、上の式の右辺を常にプラスにするような関数を選ぶ必要がある。ポアソン回帰では一般的に対数関数をリンク関数として用いる。

R によるポアソン回帰のパラメーター推定

R ではポアソン回帰を含む一般化線形モデルのパラメーターを推定する時、glm 関数を用いる。ここで、ポアソン回帰モデルのパラメーター推定を行うので、誤差構造をポアソン分布に、リンク関数を対数関数に指定する。ただし、島の面積をそのまま使用すると、面積のスケールが大きすぎてうまく回帰できないので、ここでは面積を対数化してからモデルに入力する。また、そのまま対数化すると、島の面積 1 km² 未満のときは対数化面積がマイナスの値になる。これを避けるために、島の面積の単位を m² にしてから対数化を行うことにする。

x <- log10(gala$Area * 1000000)
y <- gala$Species

m <- glm(y ~ x, family = poisson(link = "log"))

summary(m)
## Call:
## glm(formula = y ~ x, family = poisson(link = "log"))
## Deviance Residuals:
##      Min        1Q    Median        3Q       Max
## -10.4688   -3.6073   -0.8874    2.9028   10.1517
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.39281    0.13694  -10.17   <2e-16 ***
## x            0.77767    0.01647   47.21   <2e-16 ***
## ---
## Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## (Dispersion parameter for poisson family taken to be 1)
##     Null deviance: 3510.73  on 29  degrees of freedom
## Residual deviance:  651.67  on 28  degrees of freedom
## AIC: 816.5
## Number of Fisher Scoring iterations: 5

Coefficients の項目をみると (Intercept) と x の値は、それぞれ -1.39281 と 0.77767 である。この数値をポアソン回帰のモデル式に代入すると次のようになる。

これを利用して、ポアソン回帰線を散布図に書き入れると以下のようになる。

plot(x, y, xlab = "log10(Area)", ylab = "Species")

x.new <- seq(2, 10, 0.1)
lines(x.new, exp(cbind(1, x.new) %*% coef(m)))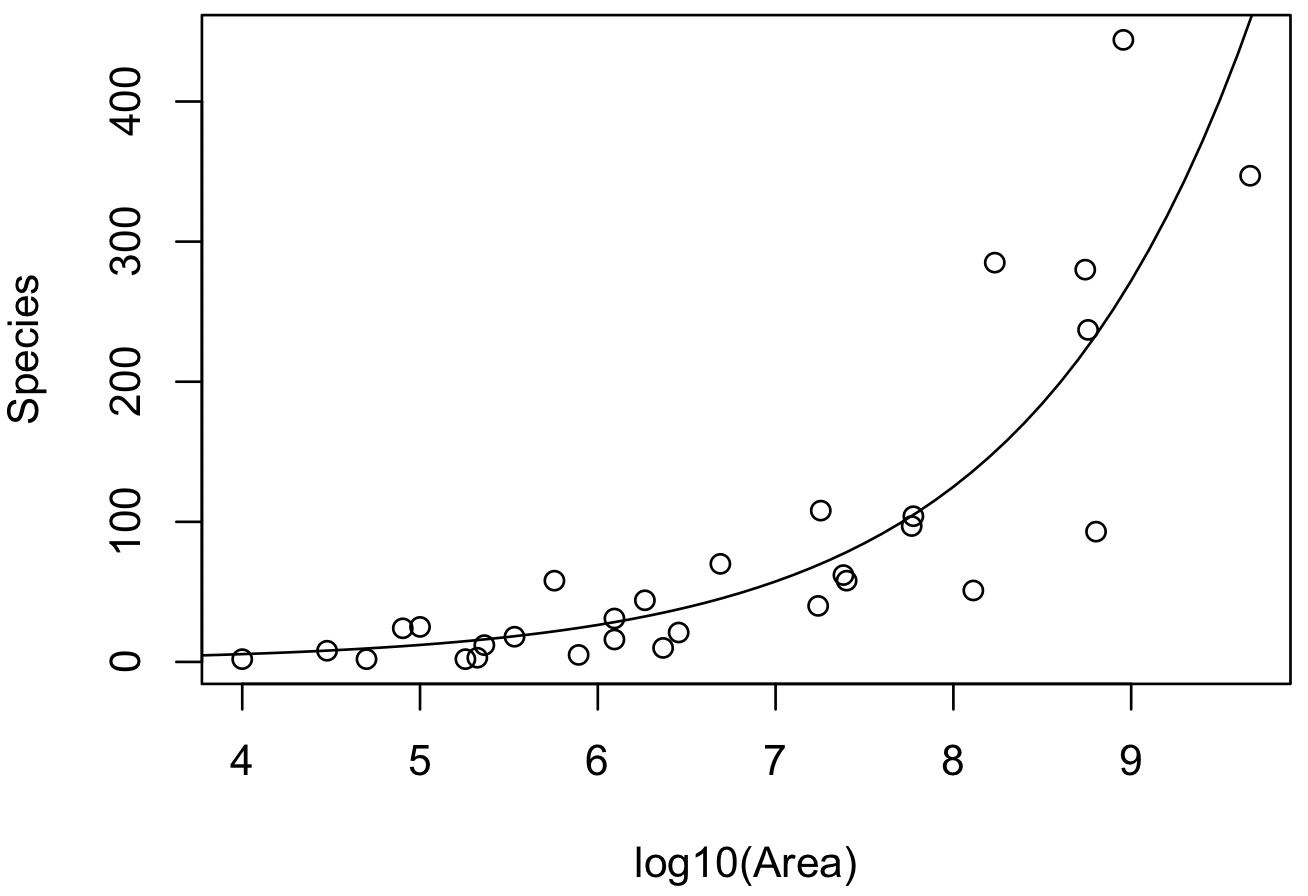

推定されたパラメータの信頼区間も図示する場合、自分で信頼区間を計算する必要がある。この場合、predict 関数で、type = 'link' を指定して、線型予測子（Xβ）の標準誤差を計算するようにする。次に、線型予測子の期待値と標準誤差を利用して、95% 信頼区間の上限と下限を計算する。

y.predicted <- predict(m, newdata = data.frame(x = x.new), type = 'link', se.fit = TRUE)

alpha <- 0.05
ci.upper <- y.predicted$fit + (qnorm(1 - alpha / 2) * y.predicted$se.fit)
ci.lower <- y.predicted$fit - (qnorm(1 - alpha / 2) * y.predicted$se.fit)

lines(x.new, exp(ci.upper), col = 'darkgray')
lines(x.new, exp(ci.lower), col = 'darkgray')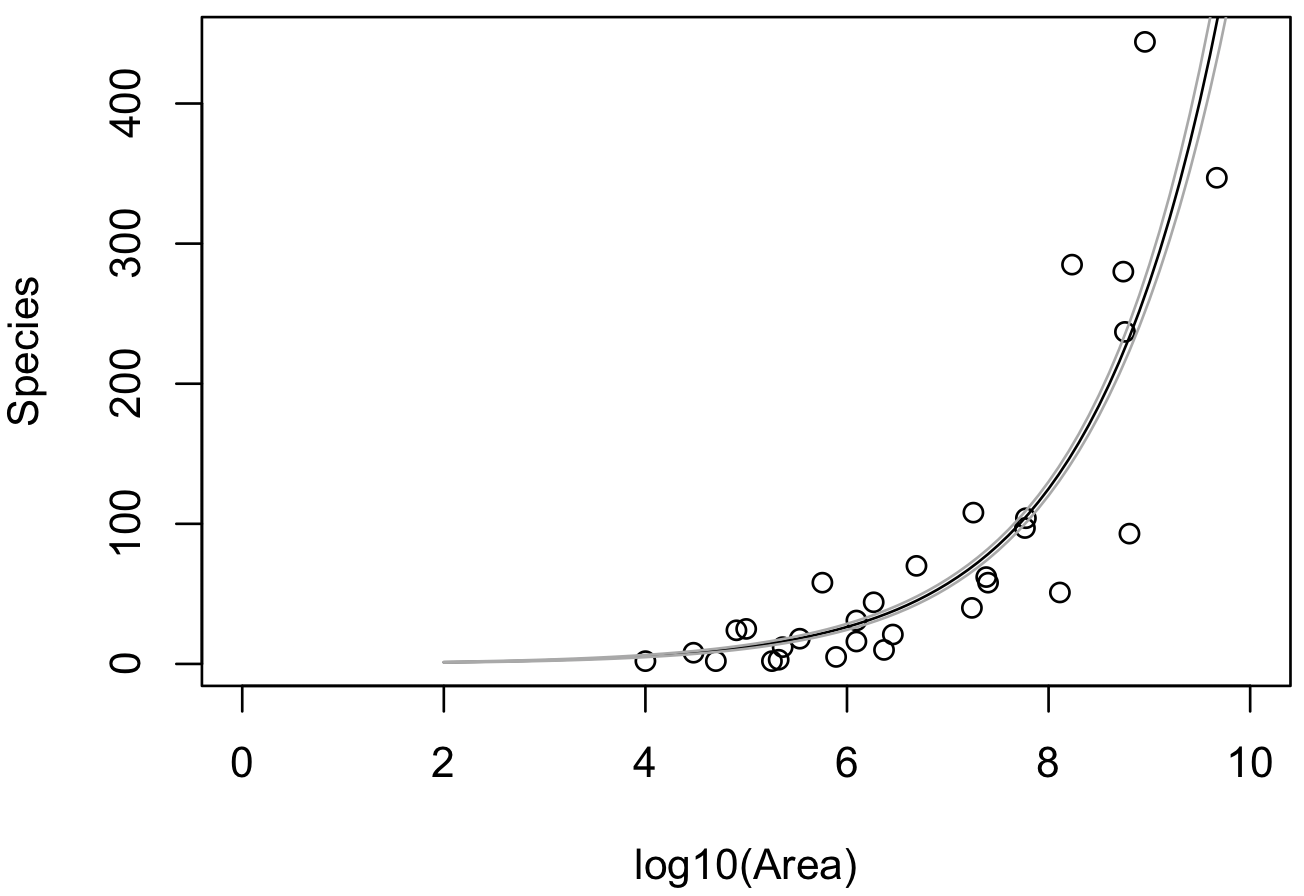

上の図からわかるように 95% 信頼区間が非常に狭い。また、図に示していないが、予測区間についても非常に狭くなっている。つまり、観測値の多くは予測区間の外側にある状態となっている。このとこから、このデータをポアソン回帰でモデル化すると、過分散問題が生じる。そのため、このデータに関して負の二項回帰などの大きな分散を許容する確率分布でモデル化することがふさわしい。