生物統計学

Bridge

モデルのパラメーターを最小二乗法で推定するとき、データのサンプル数が少なかったり、あるいは互いに相関が高い説明変数が複数存在したりする場合は、最小二乗推定量が存在しない。このとき、パラメーターに対して何らかの制約条件を与えることで、最小二乗推定量に近い値が推定されるようになる。制約条件として、パラメーターのノルムが使われることがある。比較的によく使われている制約条件として L1 ノルムと L2 ノルムがある。L1 ノルムを制約条件として用いた場合のパラメーター推定は LASSO とよばれている。また、L2 ノルムを制約条件として用いた場合のパラメーター推定は Ridge とよばれている。

Bridge

一般に p 次のノルム（Lp ノルム）を制約条件として用いたパラメーター推定は Bridge とよばれている。制約条件として Lp ノルムの与え方を説明するために、まず簡単な回帰モデルを考える。説明変数を X とし、目的変数を y とする。また、パラメーターを β とする。このとき、この回帰モデルは次式で書き表すことができる。

\[ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon} \qquad \boldsymbol{\beta} = \begin{pmatrix} \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{n} \end{pmatrix} \]

このモデルにおいてパラメーターの p 次のノルムは次のように定義される。

\[ ||\boldsymbol{\beta}||_{p}^{p} = \sqrt[p]{||\beta_{1}||^{p} + ||\beta_{2}||^{p} + \cdots + ||\beta_{n}||^{p}} \]

最小二乗推定による回帰モデルのパラメーター推定は、モデルの計算値 Xβ と実際の観測値 y の二乗誤差が最も小さくなるようにパラメーターを求めることである。これを式で書き表すと次のようになる。

\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ || \mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\} \]

このパラメーター推定式に対して、Lp ノルムを制約条件として与えると、任意の定数を t とおくと、パラメーターの推測値は \( ||\boldsymbol{\beta}||_{p}^{p} \le t \) をも満たす必要がでてくる。このとき、t を無限に大きな値にすると、実質制約条件を与えていないときと同じ状況になる。逆に t を限りなく 0 に近づけると、ほぼすべてのパラメーターが 0 となる。このように、t は制限条件の寄与を調整するためのパラメーターである。制約条件を与えるとき、あらかじめ t の値を決めておく必要がある。

\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ || \mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\} \quad \text{subject to} \quad ||\boldsymbol{\beta}||_{p}^{p} \le t \]

上記のパラメーターの推定式をラグランジュの未定乗数法を用いて書くと次のようにある。このとき、λ は正則化パラメーターと呼ばれて、t の逆数と同じ効果を持つ。つまり、λ → 0 (t → ∞) ならば制約条件を与えていないときと同じ状況になり、逆に λ → ∞ (t → 0) ならばほぼすべてのパラメーターが 0 となる。

\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ ||\mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} + \lambda ||\boldsymbol{\beta}||_{p}^{p} \right\} \]

スパース推定

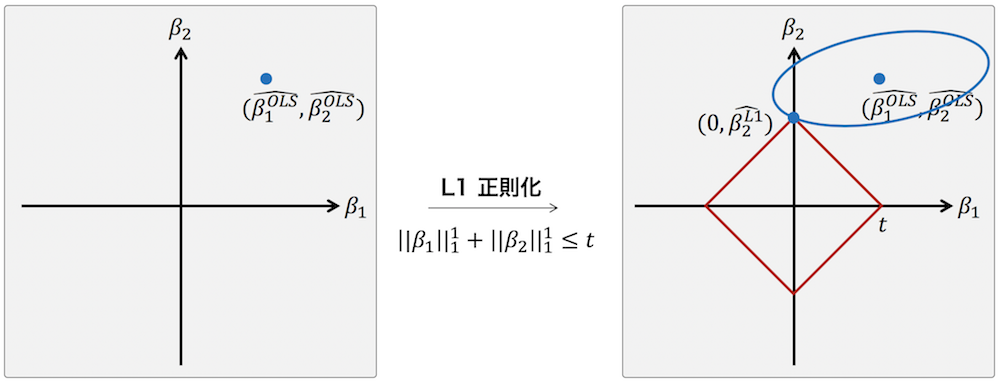
スパース推定が可能となるのは、ある βj = 0 かつ βi≠j ≠ 0 となるような点が存在することである。具体例を示すために、2 つのパラメーター β1 および β2 のみを持つ簡単な線形回帰モデルを考える。このモデルのパラメーターを最小二乗推定により推定すると、下の右図のように β1OLS および β2OLS になったと仮定する。次に、このモデルのパラメーターを最小二乗推定するときに L1 ノルムを制約条件として与えることで、パラメーターの取りうる値は下の右図の赤枠内に制限される。そして、t の値をうまく選ぶことで、下の右図のように、β1 = 0 かつ β2 ≠ 0 となる点が見つかる。このとき、β1 = 0 と推定され、パラメーターの推定結果がスパースになる。スパース推定はこのような仕組みで行われている。

L1 ノルムを制約条件としてLASSO回帰を行ったときにパラメーターの推定値（解）はスパースになる。

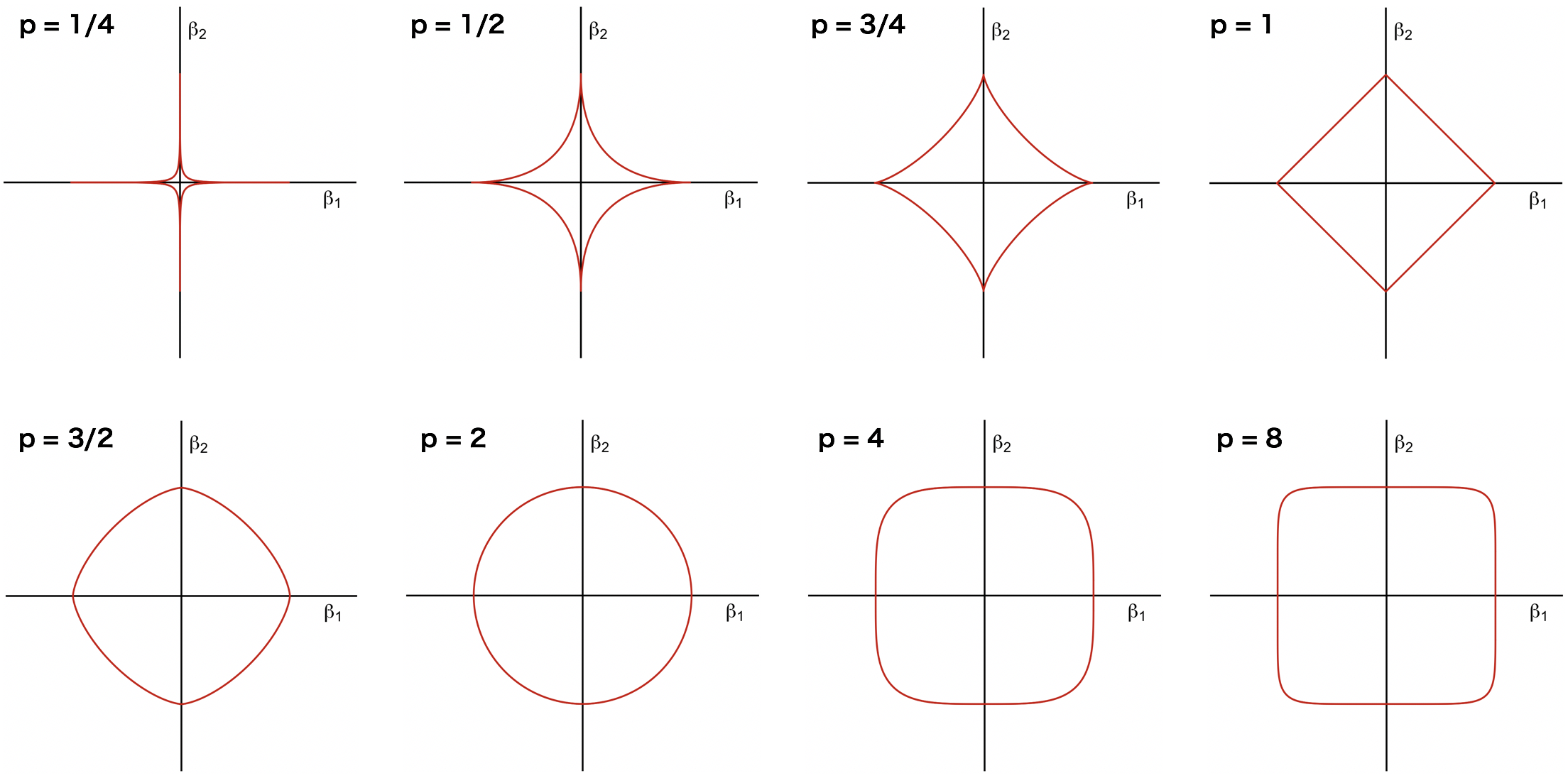
スパース推定できるのは、上述のように、ある βj = 0 かつ βi≠j ≠ 0 となるような点が存在することである。ここで、p = 1/4, 1/2, 3/4, 1, 3/2, 2, 4, 8 のときの制約条件を図示すると次のようになる。これらのグラフから、0 < p ≤ 1 のときに、解をスパースにできる機会が多いことが確認できる。とくに、0 < p < 1 のとき、p = 1 よりも解をスパースにできる機会が多い。しかし、0 < p < 1 のときは非凸関数となるため、パラメーターの推定が非常に困難となる。このため、スパース推定は p = 1 のときの L1 ノルムを制約条件として利用する LASSO がよく使われている。

Lpノルムの概形（スパース推定可能）

Lp ノルム制約条件の範囲

R で Lp ノルム制約条件の範囲を描くには、次のスクリプトを使う。

plot.LpNorm <- function(p) {
  # adjust device environment
  par(pty = 's')
  par(mar = c(1, 1, 1, 1))
  
  # prepare a blank device
  plot(0, 0, type = 'n', xlim = c(-1.5, 1.5), ylim = c(-1.5, 1.5), axes = FALSE,
       xlab = expression(beta[1]), ylab = expression(beta[2]))

  # plot lines: y = 0 and x = 0  
  abline(v = 0, lwd = 2)
  abline(h = 0, lwd = 2)  

  # plot Lp Norm curve
  beta1 <- seq(-1, 1, 0.0001)
  beta2 <- seq(-1, 1, 0.0001)
  lines(beta1, (1^p - abs(beta1)^p)^(1/p), col = '#CC0000', lwd = 2)
  lines(beta1, -(1^p - abs(beta1)^p)^(1/p), col = '#CC0000', lwd = 2)
  text(1.4, -0.16, expression(beta[1]), cex = 1.4)
  text(0.16, 1.4, expression(beta[2]), cex = 1.4)
}

plot.LpNorm(1/2)
plot.LpNorm(1)
plot.LpNorm(2)

References

  • lldiko E. Frank, Jerome H. Friedman. A statistical view of some chemometrics regression tools. J. Technometrics 1993, 35(2):109-135. DOI: 10.1080/00401706.1993.10485033