LASSO（Tibshirani, 1996）と Elastic Net（Zou et al, 2005）は、統計モデル式中の変数選択に利用されることがある。統計モデルのなかに含まれる複数のパラメータにペナルティをつけることによって、重要でないパラメータが次々と取り除くことが可能である。ペナルティのつけ方として、L1 正則化と L2 正則化などが一般的に用いられている。

L1 正則化は次のようにして、パラメーターベクトルの β を推測する。λ は正則化パラメーターを表し、λ が大きいほどモデルがシンプルになり、λ が小さいほどモデルが複雑になる。λ = 0 のとき、パラメーターの推定値は最小二乗法と同じ推定値になる。

L2 正則化は次のようにして、パラメーターベクトルの β を推測する。λ は正則化パラメーターを表す。

回帰モデルのパラメーターを推定する時、ペナルティとして L1 正則化を用い他場合に、LASSO 推定（LASSO 回帰）とよばれる。他方で、ペナルティとして L2 正則化を用いるパラメーター推定は、Ridge 推定とよばれる。また、L1 正則化と L2 正則化を任意の割合で混合させた推測方法は Elastic Net とよばれている。式に表すと、次のようになる。

R を利用して LASSO 推定などを行うには、glmnet パッケージを利用する（Hastie et al., 2016）。

ここで、LASSO 推定などに利用するサンプルデータを作成する。独立変数を 5 つ（x1, x2, x3, x4, x5）用意する。また、従属変数を Y = 4x₁ - 2x₂ + x₅ となるように作成する。変数選択がうまく行われれば、x3 と x4 の推定値が 0 になるはずである。

x1 <- rpois(1000, 5)
x2 <- rnorm(1000, 20, 3)
x3 <- x2 + rnorm(1000, 0, 1)
x4 <- x1 + x2 + rnorm(1000, 0, 1)
x5 <- rnbinom(1000, 10, 0.5)
X <- cbind(x1, x2, x3, x4, x5)
Y <- 4 * x1 - 2 * x2 + x5 + rnorm(1000, 0, 1)

LASSO

LASSO 推定は、R の glmnet パッケージ中の glmnet 関数を利用する。glmnet 関数を利用する時、 α を 1 に指定する（α > 1 の場合は、Elastic Net になる）。また、LASSO 推定を行うには、正則化パラメータ λ を指定する必要がある。一般に、クロスバリデーションにより、推定値と観測値の平均二乗誤差が最小となるように λ を決定する。

ここで、cv.glmnet 関数を利用して、クロスバリデーションにより最適な λ を見つける。cv.glmnet 関数のデフォルトでは、10-foldで、逸脱度（deviance）をクロスバリデーションの評価に利用している。クロスバリデーションの実行には多くの時間を要する。そのため、並列計算を行うパッケージ doMC や snow などを利用するとよい。

library(glmnet)
lasso.model.cv <- cv.glmnet(x = X, y = Y, family = "gaussian", alpha = 1)
## lasso.model.cv <- cv.glmnet(x = X, y = Y, family = "gaussian", alpha = 1, nfold = 5, type.measure = "deviance")
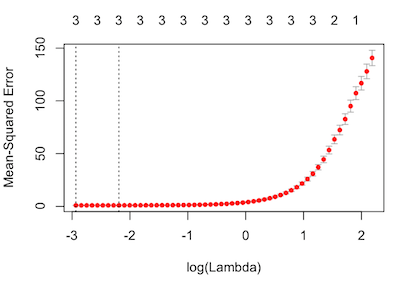
plot(lasso.model.cv)
lasso.model.cv$lambda.min
## [1] 0.05325009

λ の値と平均二乗誤差の関係を示したプロットをみると、平均二乗誤差を最小にする λ は 0.05325009 であることが確認できる。また、このときのパラメーター数は 3 つであることがわかった。

次に、この最適な λ = 0.05325009 を利用して、モデルを作成する。

lasso.model <- glmnet(x = X, y = Y, family = "gaussian", lambda = 0.05325009, alpha = 1)
lasso.model$beta
##            s0
## x1  3.9580543
## x2 -1.9763906
## x3  .
## x4  .
## x5  0.9835511

LASSO 推定の結果をみると、およそ Y = 4x₁ - 2x₂ + x₅ とみなすことができる。これは、サンプルデータを作成する時に利用した数式と同じであることがわかる。また、x2 と x1 に相関の高い x3 と x4 が取り除かれた（推定値が 0）ことがわかる。

Ridge

glmnet 関数で Ridge 推測を行うには、α をゼロに設定する。また、最適な正則化パラメータ λ を決定するには、クロスバリデーションを行うのが一般てである。

library(glmnet)
ridge.model.cv <- cv.glmnet(x = X, y = Y, family = "gaussian", alpha = 0)
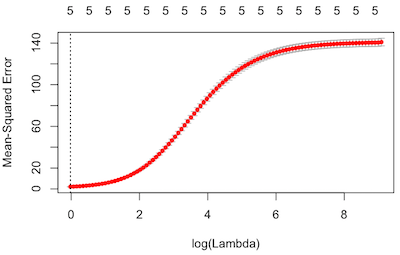
plot(ridge.model.cv)
ridge.model.cv$lambda.min
## [1] 0.9748698

平均二乗誤差を最小にする λ は 0.9748698 であることがわかり、この値を利用してモデルを作成していく。なお、Ridge 推定では、LASSO 推定とは異なり、パラメータの値をゼロにすることは難しい。

ridge.model <- glmnet(x = X, y = Y, family = "gaussian", lambda = 0.9748698, alpha = 0)
ridge.model$beta
## 5 x 1 sparse Matrix of class "dgCMatrix"
##            s0
## x1  3.5464086
## x2 -1.4479859
## x3 -0.5785474
## x4  0.1391204
## x5  0.9231415

Ridge 推定結果をみると、 x2 の係数が約 -1.5 で、x3 の係数が約 -0.5 となっていることがわかる。x3 は x2 にノイズを少し加えたものとして考えれば、両者はほぼ同じ値をとると考えられる。x2 と x3 のように、相関の高いパラメーターが存在するとき、Ridge 推定はパラメータ推定をうまく行えない。

Elastic Net

Elastic Net は Ridge 推定と LASSO 推定を割合 α で混合したものである。glmnet 関数を利用して Elastic Net 推定を行うには、α を 0 より大きく、1 より小さい値に指定する必要がある。最適な α はクロスバリデーションによって決めるのが一般である。

具体的に、0 から 1 の間に等間隔な実数値を用意し、これを α とする。次に、1 つの α に対して、cv.glmnet 関数を実行し、平均二乗誤差を最小にする λ を求める。この作業をすべての α に対して行い、最終的に、平均二乗誤差を最小にする最適な α と λ を見つける。R で行うには次のようにする。

library(glmnet)
alpha <- seq(0.01, 0.99, 0.01)
mse.df <- NULL

for (i in 1:length(alpha)) {
    m <- cv.glmnet(x = X, y = Y, family = "gaussian", alpha = alpha[i])
    mse.df <- rbind(mse.df, data.frame(alpha = alpha[i],
                                       mse = min(m$cvm)))
}

best.alpha <- mse.df$alpha[mse.df$mse == min(mse.df$mse)]

m <- cv.glmnet(x = X, y = Y, family = "gaussian", alpha = best.alpha)

best.lambda <- m$lambda.min

次に、最適な α と λ の組み合わせを利用して Elastic Net 推定を行う。

en.model <- glmnet(x = X, y = Y, family = "gaussian",
                   lambda = best.lambda, alpha = best.alpha)
en.model$beta
## 5 x 1 sparse Matrix of class "dgCMatrix"
##            s0
## x1  3.9577563
## x2 -1.9770722
## x3  .
## x4  .
## x5  0.9844043

この推定結果をみると、およそ Y = 4x₁ - 2x₂ + x₅ とみなすことができる。これは、サンプルデータを作成する時に利用した数式と同じであることがわかる。