複数の遺伝子発現プロファイルが渡されたときに、遺伝子共発現ネットワークを構築することができる。例えば、発現プロファイルの似ている遺伝子同士を近くで結びつき、発現プロファイルの異なる遺伝子をできるだけ遠くに配置するようにするネットワークを構築することができる。
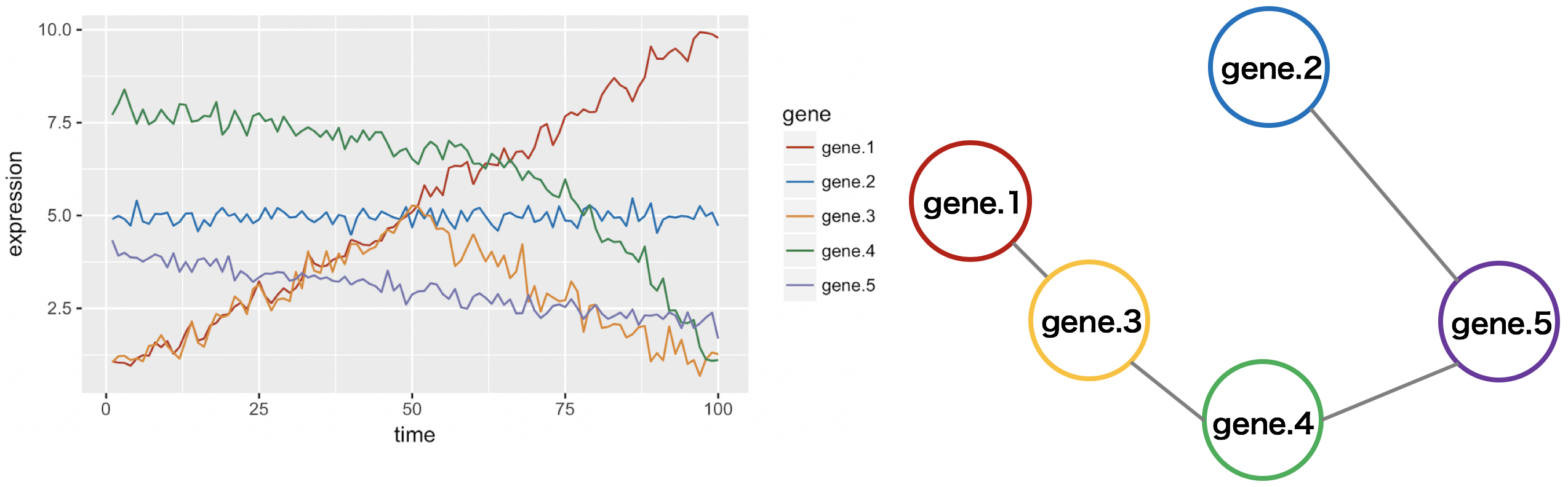
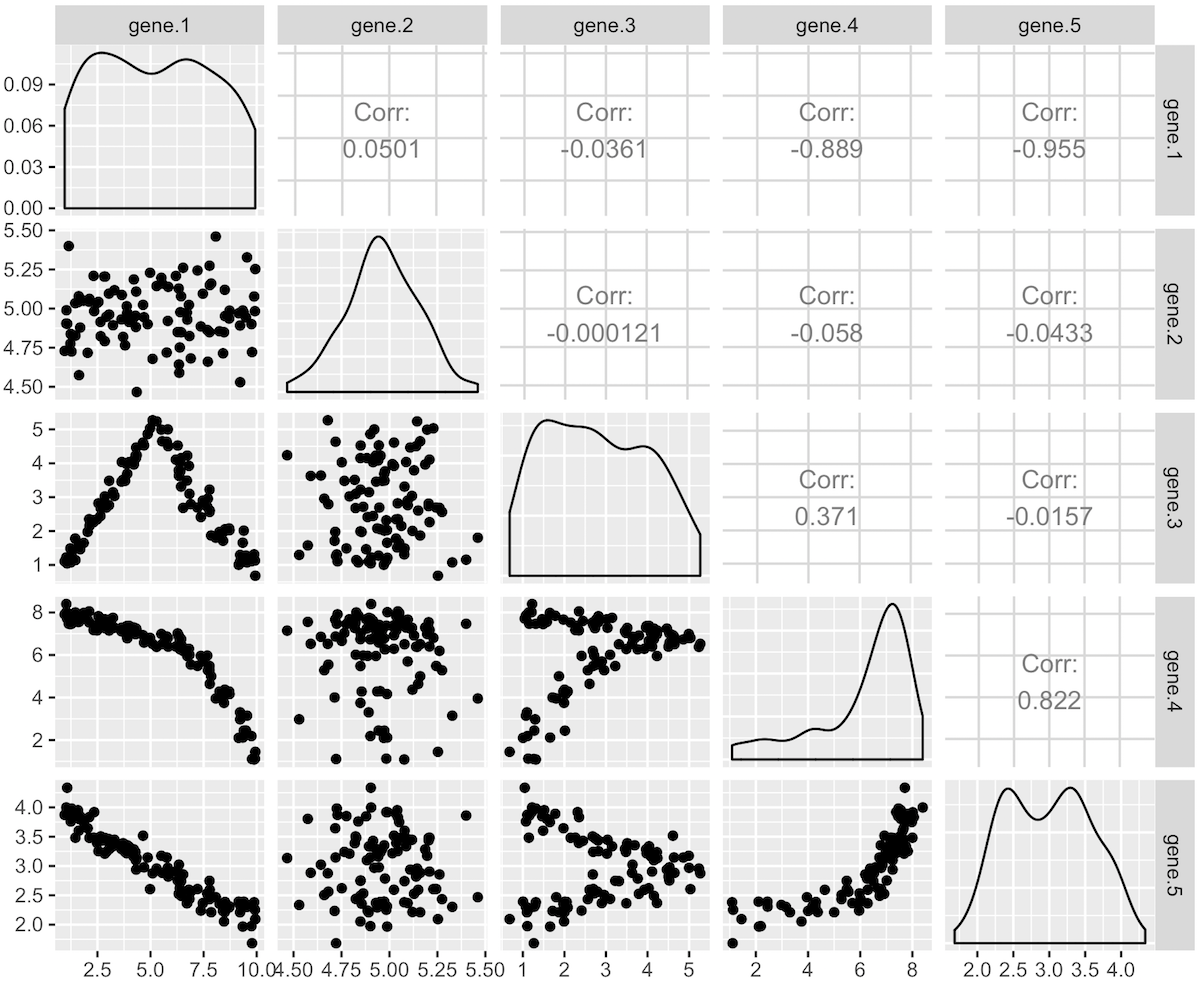
遺伝子共発現ネットワークを構築するとき、遺伝子発現プロファイル同士の相関係数に着目する方法がある。しかし、この方法は、発現プロファイル同士が完全相関あるいは完全逆相関のときにおいてのみ有効である。例えば、次の図のように gene.1 と gene.3 のプロファイルのように、前半ではほぼ同じ値であるにも関わらず、プロファイル全体では相関係数が 0.0361 となり、ほとんど相関していないという結果となった。このようなケースにおいて、相関係数は指標として信頼できなくなる。
ガウシアングラフィカルモデル
相関係数の代わりとなるネットワーク構築のアプローチがいくつか提案されている。そのうちの 1 つがガウシアングラフィカルモデルである。2 つの変数が相関していない、言い換えれば、2 つの確率変数が統計的に独立であるということである。ガウシアングラフィカルモデルでは、確率変数間の統計的な独立性に着目して、ネットワークを構築する方法である。
独立性を測る指標として共分散を用いている。2 つの確率変数の共分散を考えたとき、共分散が大きな正の値をとるとき、片方の確率変数が増加するともう片方の確率変数も増加する。逆に、共分散が大きな負の値をとるとき、片方の確率変数が増加すると、もう片方の確率変数は減少する。共分散が 0 に近い値をとるとき、両者の確率変数は互いに独立する。
ガウシアングラフィカルモデルでは、各遺伝子プロファイルをそれぞれ確率変数 x1、x2、...、xn とみなして、これらの確率変数は、多変量正規分布に従うものと仮定している。これを式で表すと、以下のようになる。ここで、X = (x1, x2, ..., xn) とし、μ を平均とし、Σ を分散共分散行列とし、|Σ| を Σ の行列式とする。
\[ \mathbf{X} \sim \mathscr{N} (\boldsymbol{\mu}, \boldsymbol{\Sigma}) \equiv \sqrt{\frac{|\Sigma^{-1}|}{(2\pi)^{n}}} \exp \left\{ -\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^{T}\Sigma^{-1}((\mathbf{x} - \boldsymbol{\mu})) \right\}\]ここで、Λ = Σ-1 となる Λ を導入する。これを精度行列という。精度行列に関して、精度行列の (i,j) 要素が 0 ならば、確率変数 xi と確率変数 xj が無関係になる性質を持つ。例えば、x3, x4, ..., xn が与えられたとき、x1 と x2 の同時確率分布は、次のように求められる。Λ12 = Λ21 であること考慮して、式を整形している。
\[ \begin{eqnarray} p(\mathbf{x}_{1}, \mathbf{x}_{2}|\mathbf{x}_{3}, \mathbf{x}_{4}, \cdots, \mathbf{x}_{n}) &=& \frac{p(\mathbf{x}_{1}, \mathbf{x}_{2}, \mathbf{x}_{3}, \mathbf{x}_{4}, \cdots, \mathbf{x}_{n})}{p(\mathbf{x}_{3}, \mathbf{x}_{4}, \cdots, \mathbf{x}_{n})} \\ &\propto & \exp \left \{ -\frac{1}{2} \left( \Lambda_{11}\mathbf{x}_{1}^{2} + 2\Lambda_{12} \mathbf{x}_{1}\mathbf{x}_{2} + \Lambda_{22}\mathbf{x}_{2}^{2} \right) \right \} \end{eqnarray} \]もし、x1 と x2 が独立ならば、x1 と x2 の同時確率分布は、p(x1) と p(x2) の積として書き表わせる必要がある。これを満たすのは、Λ12 = 0 のときに限る。つまり、Λ12 = 0 のとき、x1 と x2 は無関係であるといえる。このように、精度行列は、分散共分散行列同様に、各変数間の関係性を測る指標として使うことができる。
与えられた確率変数から精度行列を推定できれば、確率変数間の関係も明らかとなり、変数間のネットワーク構造も構築できるようになる。今、確率変数 x1、x2、...、xn が与えられたとき、その精度行列は、最尤法により、次のように求めることができる。ここでは \(\mathbf{S} = \frac{1}{n}\mathbf{X}\mathbf{X}^{T}\) とする。
\[ \begin{eqnarray} \log \prod_{i=1}^{n} \mathscr{N}(\mathbf{0}, \boldsymbol{\lambda}) &=& \sum_{i=1}^{n}\left\{ \frac{n}{2} \log(2\pi) + \frac{1}{2}\log |\boldsymbol{\Lambda}| - \frac{1}{2}\mathbf{x}^{(n)^{T}} \boldsymbol{\Lambda}\mathbf{x}^{(n)} \right\} \\ &=& \cdots \\ &=& Const. - \frac{n}{2} \left\{ tr(\boldsymbol{\Lambda}\mathbf{S}) - \log |\boldsymbol{\Lambda}| \right\} \end{eqnarray} \]上式における尤度最大化は、次式の最小化と同等である。
\[ \hat{\boldsymbol{\Lambda}} = \arg \min_{\boldsymbol{\Lambda}} \left\{ tr(\boldsymbol{\Lambda}\mathbf{S}) - \log |\boldsymbol{\Lambda}| \right\} \]グラフィカル LASSO
グラフは精度行列から作られる。よりスパースなグラフを構築するには、よりスパースな精度行列を求める必要がある。つまり、精度行列の各要素をできるだけ 0 にするようにすれば、スパースな精度行列が求められる。そこで、上に示した最尤法より精度行列を推測する式に Λ の要素をできるだけ 0 にする正則化項を加えれば良い。
\[ \hat{\boldsymbol{\Lambda}} = \arg \min_{\boldsymbol{\Lambda}} \left\{ tr(\boldsymbol{\Lambda}\mathbf{S}) - \log |\boldsymbol{\Lambda}| + \lambda \sum_{i\ne j}|\Lambda_{ij}| \right\} \]精度行列推定時において、L 1正則化項を加えて推測する方法は、グラフィカル LASSO と呼ばれている。この推定式において、正則化パラメーター λ を大きくすすると、制約が大きくなる、精度行列の各要素が 0 になりやすくなる。これにより、求められる解がスパースになり、精度行列から作られるグラフもスパースになる。
References
- Convex optimization techniques for fitting sparse Gaussian graphical models. In Proc. Intl. Conf. Machine Learning 2006, 89-96. PDF
- Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008, 9(3):432-441. DOI: 10.1093/biostatistics/kxm045
- 依存関係にスパース性を入れる — グラフィカル lasso の話. 岩波データサイエンス 2016, 5. PDF