説明変数の属性に基づいていくつかのグループに分けられるとき、変数選択においてグループ毎に選択したい場合に group LASSO を使用する。例えば、植物にエチレンを過剰に与えたときの反応を調べるために、エチレンの濃度と植物ホルモン応答遺伝子の発現量をモデリングしようとする。植物ホルモン応答遺伝子は、エチレン応答遺伝子群、アブシジン酸応答遺伝子群、オーキシン応答遺伝子群などいくつかのグループに分けることができる。このとき、LASSO を使用してモデリングを行うと、エチレン応答遺伝子群に含まれている遺伝子がすべて選択されるとは限らない。また、他の植物ホルモン応答遺伝子群に含まれる遺伝子が選択されたりする場合もある。これに対して、group LASSO を使用してモデリングを行うと、エチレン応答遺伝子群に含まれる遺伝子がすべて選択されるようになり、他の植物ホルモン応答遺伝子群に含まれる遺伝子がまったく選択されなくなる。ただし、1 つの遺伝子が複数のグループに分けられるとき、group LASSO に比べ overlapping group LASSO が有効である。
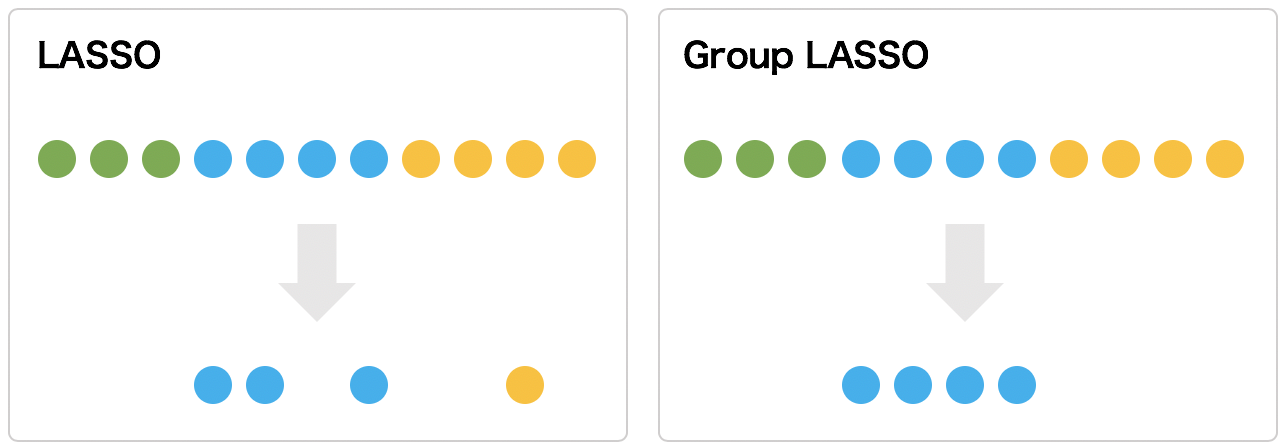
Group LASSO を説明するために簡単な回帰モデルを考える。このモデルの目的変数を y として、説明変数と X とする。また、データのサンプル数を n 個とし、説明変数の数を p 個とする。
p 個の説明変数は G 個のグループに分けられるものとする。グループ g に分けられる説明変数の個数を pg 個とする。このとき、グループ g に含まれている pg 個の説明変数だけでモデルを構築した場合は、次のようになる。ただし、Xg は n × pg の計画行列を表し、βg はグループ g に対するパラメーター(回帰係数)を表す。
\[ \mathbf{y} = \mathbf{X}_{g}\boldsymbol{\beta}_{g} + \boldsymbol{\epsilon} \]このとき、このデータセット全体に対する回帰モデルを式で表すと次のようになる。
\[ \mathbf{y} = \sum_{g=1}^{G} \mathbf{X}_{g}\boldsymbol{\beta}_{g} + \boldsymbol{\epsilon} \]この回帰モデルに対して、group LASSO では次のように正規化項を与えてパラメーター推定を行なっている。ここで Kg を正定値行列(ηTKη が正になるときの行列 K)とする。
Kg は Kg = pgIpg が用いられている。このとき、
\[ \sqrt{\boldsymbol{\beta}_{g} ^{T}K_{g}\boldsymbol{\beta}_{g}} = \sqrt{\boldsymbol{\beta}_{g} ^{T}(p_{g}\mathbf{I}_{g})\boldsymbol{\beta}_{g}} = \sqrt{p_{g}||\boldsymbol{\beta}_{g} ||^{2}_{2}} \]が成り立つので、上記のパラメーターの推定式は、次のように計算される。
ここで、\( \zeta^{2}_{g} = ||\boldsymbol{\beta}_{g} ||^{2}_{2} \) とおくと、上式は次のようにかける。つまり、グループごとに L1 正則化項を与えている式とみなすことができる。この式から、グループ g に含まれているパラメーターがすべて 0 になるときに限り、このグループ g 全体にかかる正則化項が 0 になることがわかる。これにより group LASSO はグループごとの選択を可能にしている。