まず、サンプルデータを作成する。真の説明変数として 2 つ（z₁, z₂）を作り、真の説明変数にノイズを与えて 5 つの説明変数 （x₁, x₂, x₃, x₄, x₅）を作る。また、応答変数 y を 2z₁ - z₂ にノイズを加えた値とする。

z1 <- runif(100, 0, 10)
z2 <- runif(100, 0, 10)

x1 <- z1 + rnorm(100, 0, 1)
x2 <- z1 + rnorm(100, 0, 1)
x3 <- 2 * z1 + rnorm(100, 0, 1)
x4 <- z2 + rnorm(100, 0, 1)
x5 <- - 3 * z2 + rnorm(100, 0, 1)

X <- cbind(x1, x2, x3, x4, x5)
X.scaled <- scale(X)
Y <- 2 * z1 - z2 + rnorm(100, 0, 1)

LASSO 回帰

R の glmnet パッケージの glmnet 関数を使って LASSO 回帰を行うことができる。glmnet 関数を使うとき、 α を 1 に指定する（α = 0 のときは Rdige 回帰、0 < α < 1 のときは Elastic Net になる）。LASSO 回帰を行う前に、正則化パラメーターを与える必要があるが、ここでは与えずに glmnet 関数で実行してみる。この場合、λ を与えていないので、glmnet 関数はデータセットに応じて複数の λ で試してそれらの結果を返す。

library(glmnet)
lasso.model <- glmnet(x = X.scaled, y = Y, family = "gaussian", alpha = 1)
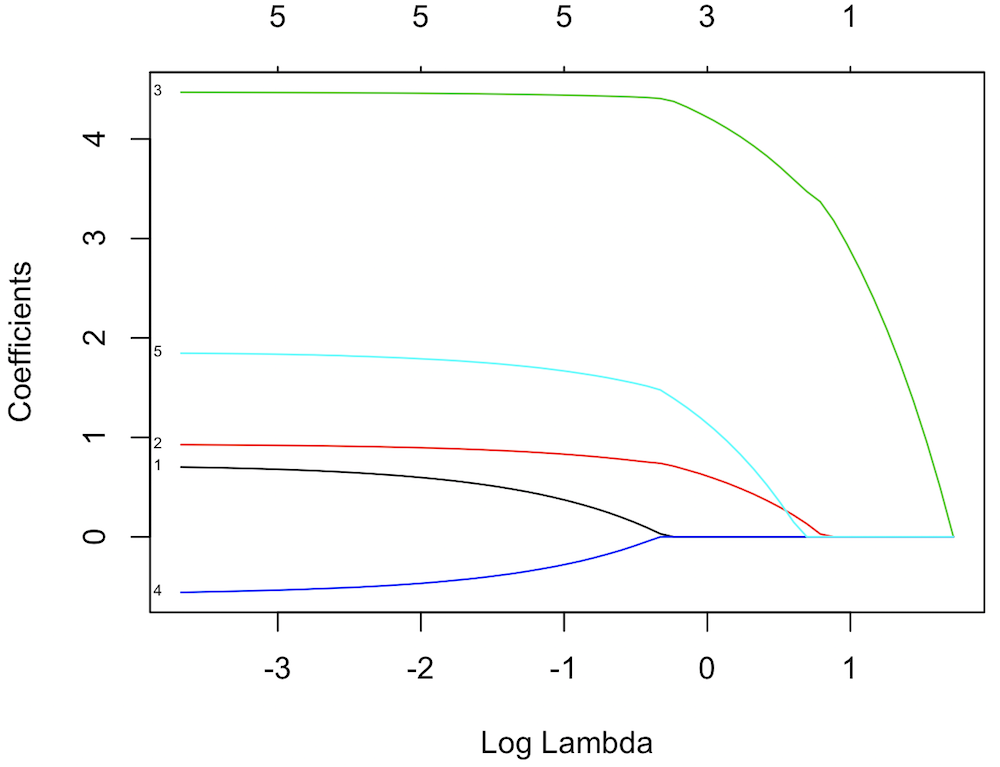
plot(lasso.model, xvar="lambda", label=TRUE)

plot 関数で glmnet の実行結果を視覚化すると、解パスと呼ばれるグラフが描かれる。このグラフの横軸は λ の値で、縦軸は各パラメーターの係数となっている。λ の値が大きいとき、正則化項の寄与が大きいのでパラメーターの係数がほとんど 0 の値をとるようになる。逆に λ の値が小さいとき、正則化項の寄与が小さく、ほとんどペナルティのない状態となるので、パラメーターは様々な値を取れるようになる。λ が 0.1 以下ならば、このモデルは 5 つのパラメーターを持つ。λ が 1 以上ならば、このモデルはパラメーターを 1 つだけ（x₃）を持つことが図から読み取れる。

クロスバリデーション

最適な λ を決めるためにはクロスバリデーションを行う必要がある。ここで、glmnet パッケージ中の cv.glmnet 関数を利用して、10-fold クロスバリデーションを行って今回のデータセットに最適な λ の値を決定しておく。

lasso.model.cv <- cv.glmnet(x = X.scaled, y = Y, family = "gaussian", alpha = 1)
plot(lasso.model.cv)
lasso.model.cv$lambda.min
## [1] 0.02778313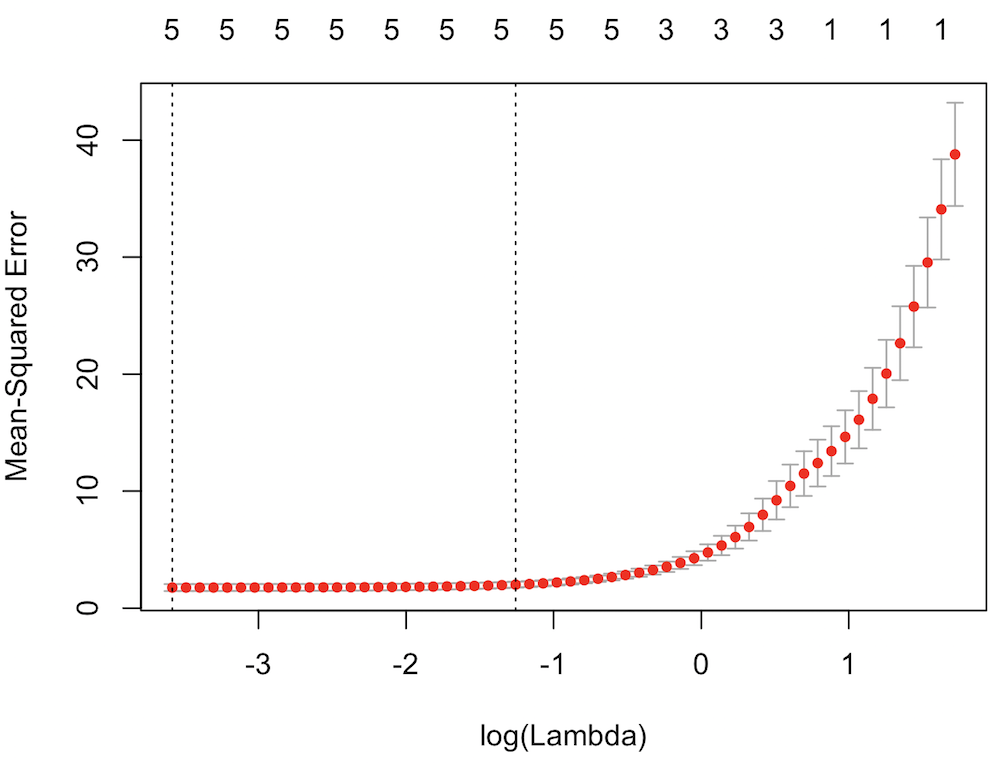

λ の値と平均二乗誤差の関係を示したプロットをみると、平均二乗誤差を最小にする λ は 0.02778313 であることが確認できる。また、このときのパラメーター数は 5 つであることがわかった。

モデル評価

LASSO 回帰によって求めら得たモデルは lasso.model に保存されている。また、クロスバリデーションでによって求められた最適な λ は lasso.model.cv$lambda.min に保存されている。これらを用いて、モデルの評価を行う。モデルで計算した値と実際の観測値の平均二乗誤差を計算してみると 1.45 とった。

※ 平均二乗誤差の値の大きさは応答変数の桁数に依存する。比較なしに、MSE が小さいからモデルの精度がよいと主張することはできない。また、応答変数（の性質など）が異なる複数のモデルを比較する際にも、平均二乗誤差を用いるときに十分注意すること。さらに、LASSO 回帰で作ったモデルを予測モデルとして精度評価を行う場合は、パラメーター推定のときとは別のデータセットを用意して検証を行う必要がある。

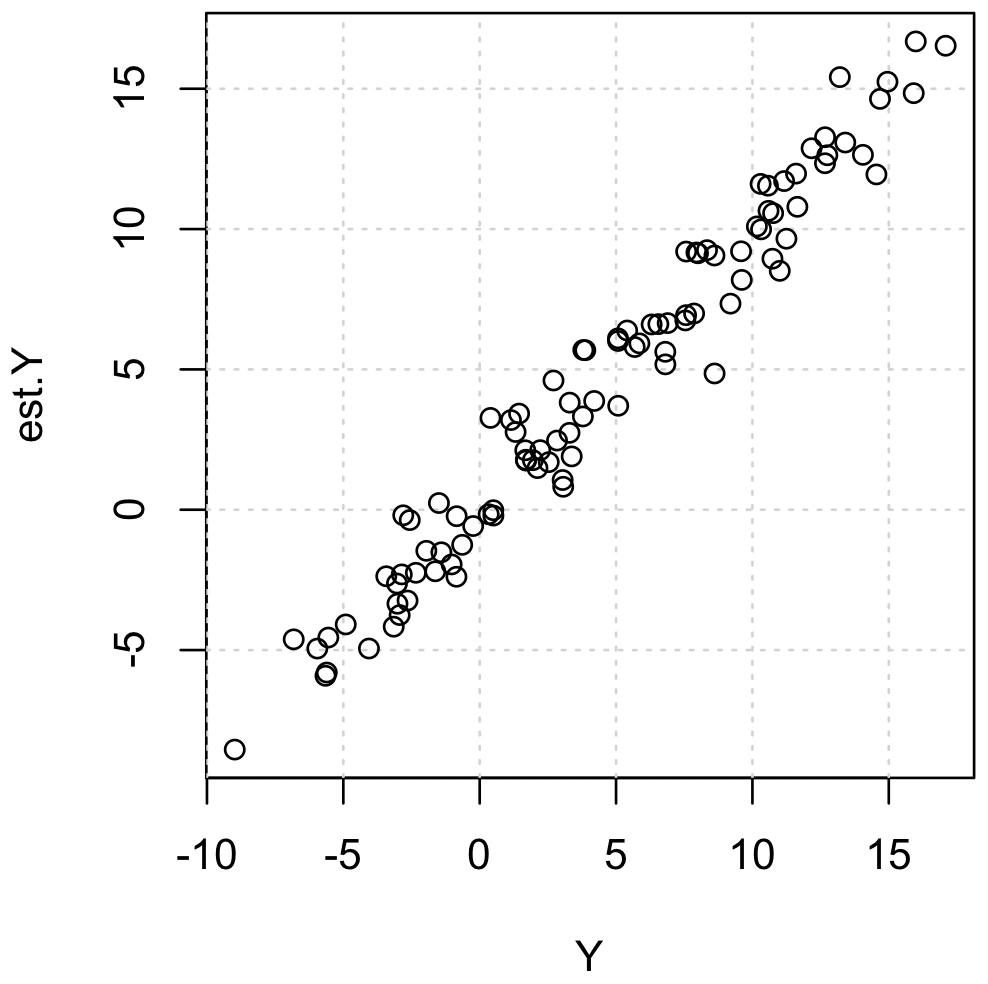
est.Y <- predict(lasso.model, newx = X.scaled, s = lasso.model.cv$lambda.min, type = 'response')
mse <- sum((Y - est.Y)^2) / length(Y)
mse
## [1] 1.447778
plot(Y, est.Y)