生物統計学

LASSO

LASSO (Least absolute shrinkage and selection operator) (Tibshirani, 1996) は、スパース推定を実現する手法の一つである。モデルのパラメーターを最小二乗法で推定するとき、データのサンプル数が少なかったり、あるいは互いに相関が高い説明変数が複数存在したりする場合は、最小二乗推定量が存在しない。このとき、パラメーターに対して L1 ノルムとよばれる制約条件を与えることで、最小二乗推定量に近い値が推定されるようになる。L1 ノルムを制約条件として用いた場合のパラメーター推定を LASSO とよぶ。

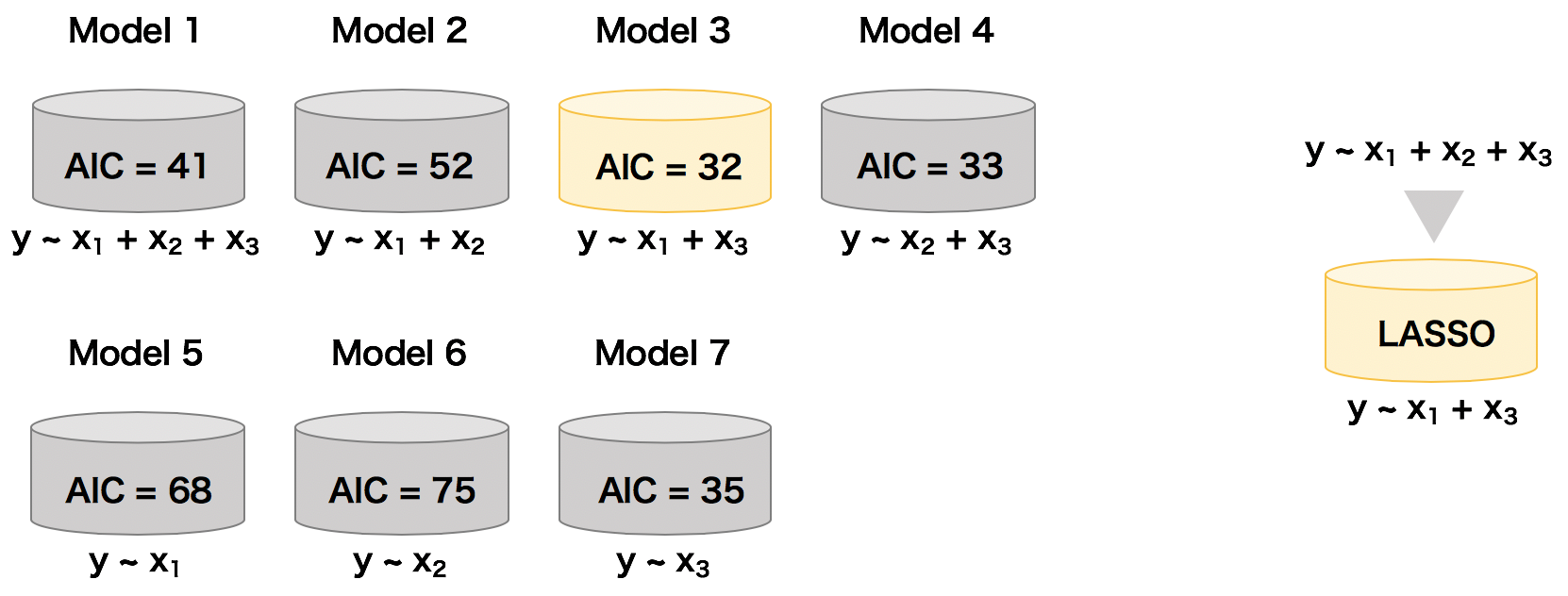
LASSO は目的変数を説明するために最適な説明変数を自動的に選択してモデルを作成している。言い換えれば、LASSO は変数選択とモデル構築を同時に行ってくれるモデリング手法である。LASSO を使えば、従来のように、異なる種類のパラメーターを含んだ複数のモデルを作成して、それらのモデルの AIC を比較して最適なモデルを決める、といった必要がなくなる。

LASSOは変数選択とモデル構築を同時に行えて、従来の手法よりも効率的にモデリングすることができる。

スパース推定

LASSO によるパラメーターのスパース推定を説明するために、簡単な回帰モデルを考える。説明変数を X とし、目的変数を y とする。また、パラメーターを β とする。このとき、この回帰モデルは次式で書き表すことができる。

\[ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon} \qquad \boldsymbol{\beta} = \begin{pmatrix} \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{n} \end{pmatrix} \]

このモデルにおいてパラメーターの L1 ノルムは次のように定義される。

\[ ||\boldsymbol{\beta}||_{1}^{1} = |\beta_{1}| + |\beta_{2}| + \cdots + |\beta_{n}|\]

最小二乗推定による回帰モデルのパラメーター推定は、モデルの計算値 Xβ と実際の観測値 y の二乗誤差が最も小さくなるようにパラメーターを求めることである。これを式で書き表すと次のようになる。

\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ || \mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\} \]

このパラメーター推定式に対して、L1 ノルムを制約条件として与えると、任意の定数を t とおくと、パラメーターの推測値は \( ||\boldsymbol{\beta}||_{1}^{1} \le t \) をも満たす必要がでてくる。このとき、t を無限に大きな値にすると、実質制約条件を与えていないときと同じ状況になる。逆に t を限りなく 0 に近づけると、ほぼすべてのパラメーターが 0 となる。このように、t は制限条件の寄与を調整するためのパラメーターである。制約条件を与えるとき、あらかじめ t の値を決めておく必要がある。

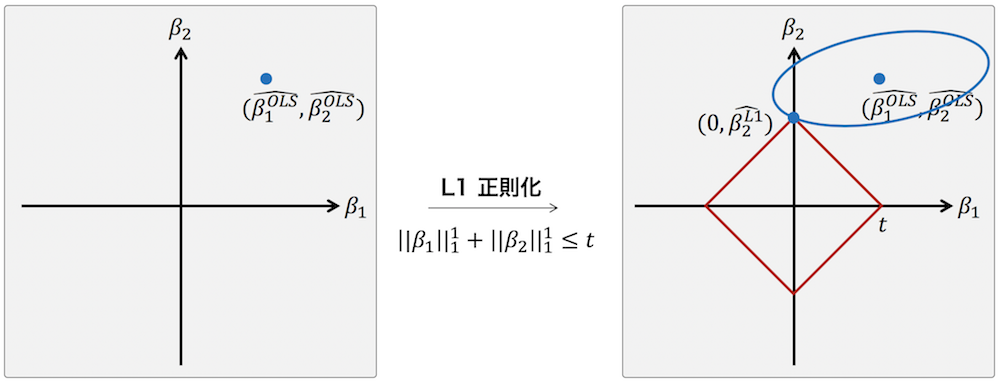
\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ || \mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\} \quad \text{subject to} \quad ||\boldsymbol{\beta}||_{1}^{1} \le t \]

パラメーター推定時に L1 ノルムを制約条件として与えた場合、推定されるパラメーターがスパースになることを説明するために、2 つのパラメーター β1 および β2 のみを持つ簡単な線形回帰モデルを考える。このモデルのパラメーターを最小二乗推定により推定すると、下の右図のように β1OLS および β2OLS になったと仮定する。次に、このモデルのパラメーターを最小二乗推定するときに L1 ノルムを制約条件として与えることで、パラメーターの取りうる値は下の右図の赤枠内に制限される。t を大きくすることで、実質制約条件がない状況と同じになるので、パラメーターの推定値は最小二乗推定量と同じになる。また、t を 0 に近づけることで、パラメーター全体が 0 となったりあるいは限りなく小さな値をとるようになる。そして、t の値をうまく選ぶことで、下の右図のように、β1 = 0 かつ β2 ≠ 0 となる点が見つかる。このとき、β1 = 0 と推定され、パラメーターの推定結果がスパースになる。LASSO はこのような仕組みで行われている。

L1 正則化のイメージ図

上記のパラメーターの推定式をラグランジュの未定乗数法を用いて書くと次のようにある。このとき、λ は正則化パラメーターと呼ばれて、t の逆数と同じ効果を持つ。つまり、λ → 0 (t → ∞) ならば制約条件を与えていないときと同じ状況になり、パラメーターの推定値は最小二乗推定量と同じものになる。逆に λ → ∞ (t → 0) ならばほぼすべてのパラメーターが 0 となる。

\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ ||\mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} + \lambda ||\boldsymbol{\beta}||_{1}^{1} \right\} \]

正則化パラメーター λ（調整パラメーター t）は、自動的に決まらない値である。LASSO によるスパース推定を行う前に、決めておく必要がある。一般的には、これをハイパーパラメーターとみなして、クロスバリデーションを通して最適な値を決めている。

過剰適合（過学習）の抑制

統計モデルあるいは機械学習モデル（予測モデル）を構築するときに、モデルのパラメーター（説明変数あるいは特徴量）を多くすることで、モデルの性能が高くなる。例えば、重回帰モデルにおいて、説明変数の数を増やすことで、モデルの平均二乗誤差を小さくすることができる。しかし、説明変数を過度に増してしまうと、構築されたモデルは手持ちのデータに過剰適合してしまい、他のデータセットに適用できなくなる。

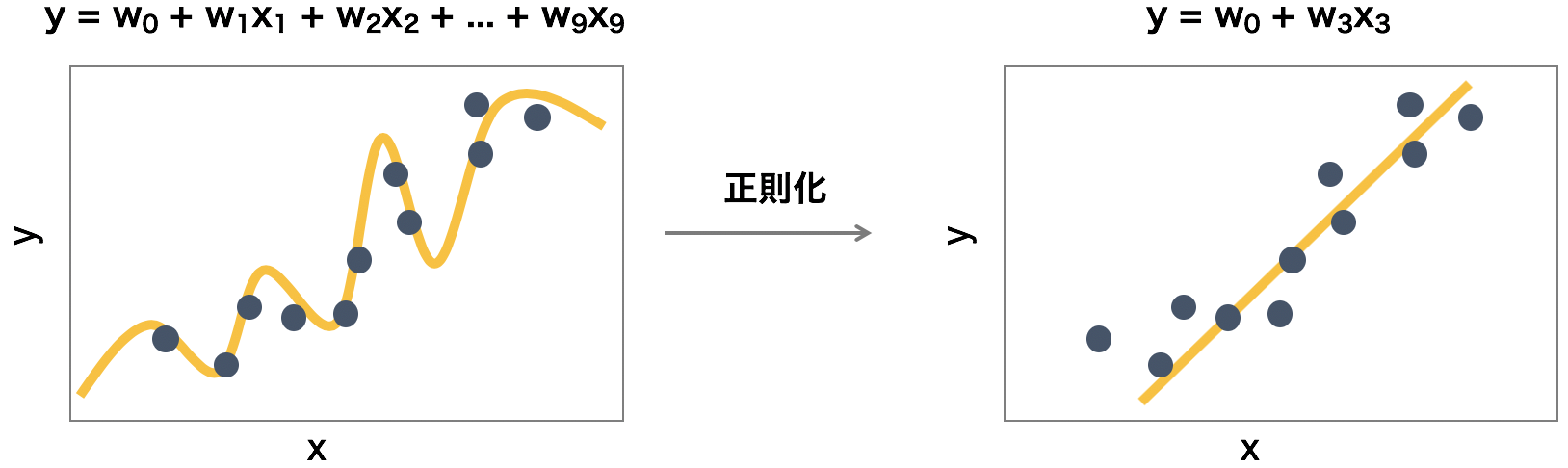
LASSO によるスパース推定はモデルの過剰適合を防ぐことができる。例えば、下の左図のように、重回帰モデルを作成すると 9 つのパラメーターを必要とする。これに対して、LASSO を用いてスパース推定を行うと、目的変数を説明するために重要と考えられるパラメーターだけが選択されてモデルが構築される。このように構築されたモデルは、重要なパラメーターしか含んでおらず、様々なデータセットに対して頑健性を持つと考えられる。

LASSOによるスパース推定はモデルの過剰適合を防ぐことができる。

LASSO の問題点

LASSO はスパース推定法として非常に有用であるが、2 つの問題点を持つ。1 つ目の問題点とは、データのサンプル数が n 個、説明変数の数が p 個のとき、p < n のとき LASSO は高々 n 個のパラメーターまでしか選択できないことである。2 つ目の問題点とは、説明変数同士の相関が高い場合、その中から 1 つしか選択されないことである。

LASSO の拡張

LASSO を用いてモデルを構築するとき、相関の高い説明変数が複数存在すると、LASSO はその中から任意に 1 つだけ選択してモデル化を行う。相関の高い説明変数が存在しているとき、それらの説明変数をすべて選択したい場合に使われるスパース推定の手法として、group LASSO、overlapping group LASSO、cluster LASSO、そして OSCAR などがある。group LASSO および overlapping group LASSO はあらかじめ説明変数のグループ情報を与える必要があるのに対して、cluster LASSO と OSCAR ではそのようなグループ情報を与える必要はない。そのため、cluster LASSO と OSCAR はクラスタリング手法としても使われている。

References