Overlapping group LASSO | 説明変数間でグループを形成しているときの変数選択

説明変数の属性に基づいていくつかのグループに分けられるとき、変数選択においてグループ毎に選択したい場合にグルーピング効果を取り入れた LASSO を使用する。そのような LASSO には group LASSO や overlapping group LASSO などがある。説明変数のグループ分けにおいて、1 つの説明変数が 1 つだけのグループに分けられるときに、group LASSO が有効である。これに対して、1 つの説明変数が複数のグループに分けられるとき、overlapping group LASSO が有効である。

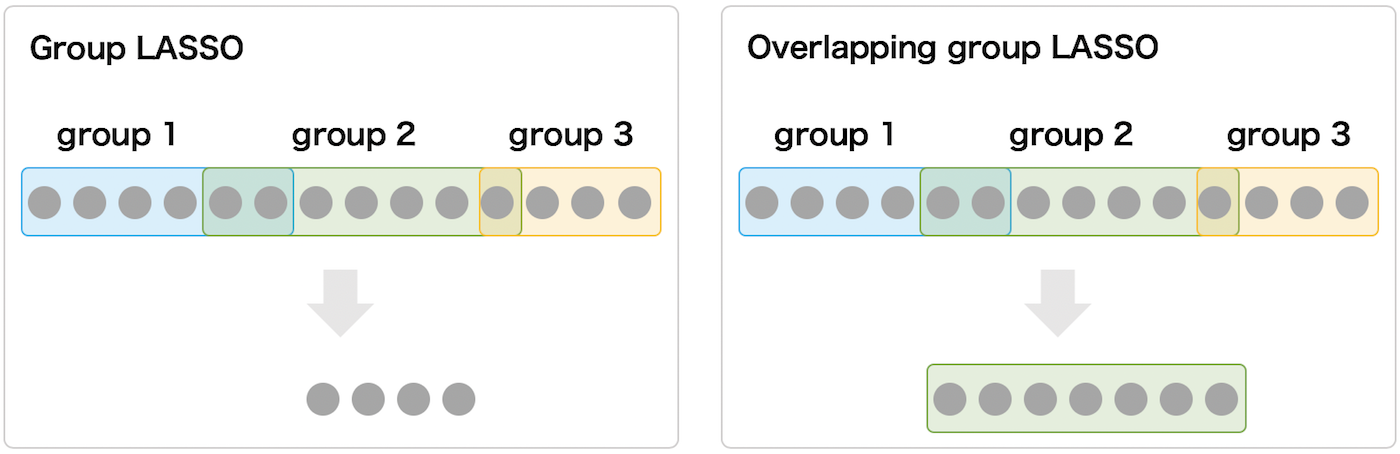
例えば、下図のように group 1, 2, 3 に分類できる 14 個の説明変数に対してスパースモデリングを行なって、重要と思われる group 2 のグループを選択したいと仮定する。このとき、group LASSO を使うと、group 1 と group 3 にかかる係数が 0 となり、group 2 にかかる係数が 0 以外の値にあると考えられる。これにより group LASSO では group 2 が選択されるが、group 2 に含まれている説明変数がいくつかかけている状態となる。これは、欠けた説明変数が、group 1 および group 3 にも分類されているために係数が 0 となったためである。これに対しして、グループ間の重なりを考慮した overlapping group LASSO を使用すると、group 2 に含まれている説明変数全体を選択できるようになる。

Overlapping group LASSO を説明するために簡単な回帰モデルを考える。このモデルの目的変数を y として、説明変数と X とする。また、データのサンプル数を n 個とし、説明変数の数を p 個とする。p 個の説明変数が G 個のグループに分けられるものとする。このとき、1 個の説明変数が複数のグループに分けられることも許可する。

次に、LASSO を行うときに正則化項として重複ありのグルーピング効果を考慮した項を与える必要がある。このような項として、p 次元の潜在変数ベクトル ν = (ν₁, ν₂, ..., ν_G) を考える。ν_g の各要素の値について、グループ g に含まれている説明変数に対応している要素（位置）の値は β と同じ値として、それ以外の要素（位置）の値を 0 とする。

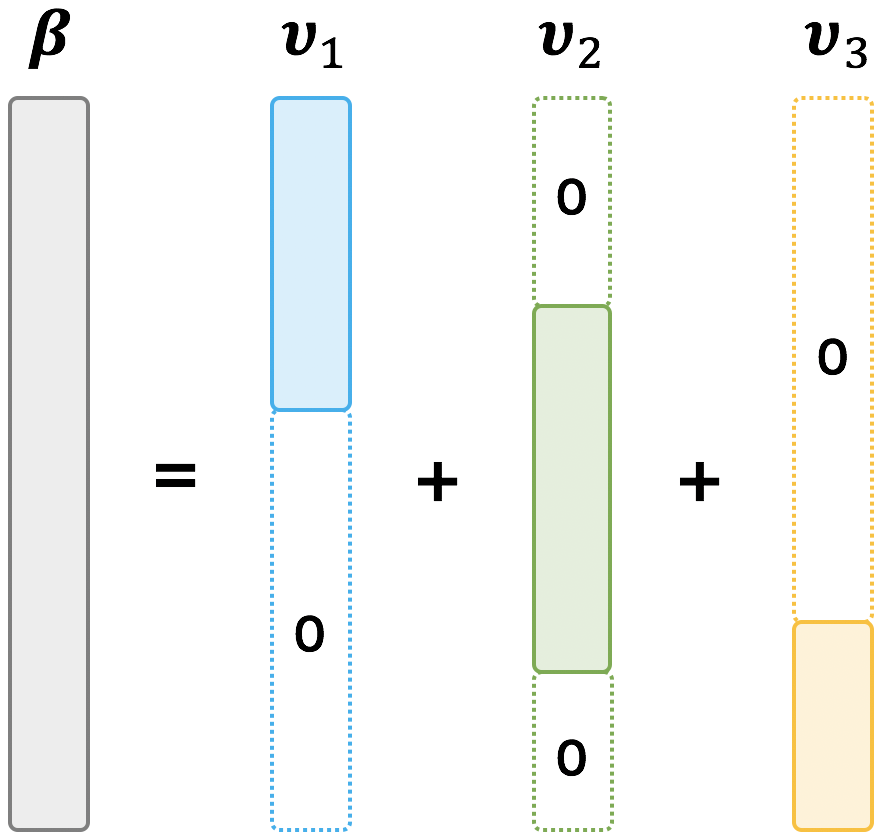
overlapping group LASSO における潜在変数ベクトルのイメージ。

例えば、上の図の例では、ベクトル ν は以下のようになる。

\[ \boldsymbol{\nu} = \begin{pmatrix} \boldsymbol{\nu}_{1} & \boldsymbol{\nu}_{2} & \boldsymbol{\nu}_{3} \\ \end{pmatrix} = \begin{pmatrix} \beta_{1} & 0 & 0 \\ \beta_{2} & 0 & 0 \\ \beta_{3} & 0 & 0 \\ \beta_{4} & 0 & 0 \\ \beta_{5} & \beta_{5} & 0 \\ \beta_{6} & \beta_{6} & 0 \\ 0 & \beta_{7} & 0 \\ 0 & \beta_{8} & 0 \\ 0 & \beta_{9} & 0 \\ 0 & \beta_{10} & 0 \\ 0 & \beta_{11} & \beta_{11} \\ 0 & 0 & \beta_{12} \\ 0 & 0 & \beta_{13} \\ 0 & 0 & \beta_{14} \\ \end{pmatrix} \]

重複ありのグルーピング効果を考慮したスパース推定では、正則化項として ||ν||₂ を設けて、||ν||₂ が最小化した上でパラメーター推定を行えばよい。これを式で表すと次のようになる。

\[ \hat{\boldsymbol{\beta}} = \arg \min_{\boldsymbol{\beta}} \left\{ ||\mathbf{y} - \sum_{g=1}^{G} \mathbf{X}_{g}\boldsymbol{\beta}_{g} ||^{2}_{2} + \lambda \left( \arg \min_{\boldsymbol{\nu}} \left\{ \sum_{g=1}^{G}||\boldsymbol{\nu}_{g}||\right\} \right) \right\} \]

ν の成分に着目すると、上式の最適化は次の式の最適化と等価である。すると、この問題は group LASSO と同様な問題に帰着できる。

\[ \hat{\boldsymbol{\nu}} = \arg \min_{\boldsymbol{\beta}} \left\{ ||\mathbf{y} - \sum_{g=1}^{G} \mathbf{X}\boldsymbol{\nu}_{g} ||^{2}_{2} + \lambda \sum_{g=1}^{G}||\boldsymbol{\nu}_{g}||_{2} \right\} \]