モデルのパラメーターを最小二乗法で推定するとき、データのサンプル数が少なかったり、あるいは互いに相関が高い説明変数が複数存在したりする場合は、最小二乗推定量が存在しない。このとき、パラメーターに対して L2 ノルムとよばれる制約条件を与えることで、最小二乗推定量に近い値が推定されるようになる。L2 ノルムを制約条件として用いた場合のパラメーター推定を Ridge (Hoerl et al., 1970) とよぶ。
Ridge によるパラメーター推定を説明するために、簡単な回帰モデルを考える。説明変数を X とし、目的変数を y とする。また、パラメーターを β とする。このとき、この回帰モデルは次式で書き表すことができる。
\[ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon} \qquad \boldsymbol{\beta} = \begin{pmatrix} \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{n} \end{pmatrix} \]回帰モデルに対して最小二乗推定によりパラメーターを推定することは、モデルの計算値と実際の観測値の二乗誤差が最も小さくなるようにパラメーターを推定することである。これを式で書き表すと、次のようになる。
\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{||\mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\} \]これを解くために、\( S(\boldsymbol{\beta}) = \frac{1}{2}||\mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \) として、各パラメーター βi に関して偏微分して、連立方程式としてとけばよい。
\[ \begin{eqnarray} && \frac{\partial S(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = -X^{T}(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) = \mathbf{0} \\ &\Longrightarrow& \hat{\boldsymbol{\beta}} = (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{y} \end{eqnarray} \]ここで、β が求まるには、XTX の逆行列が存在する必要がある。しかし、説明変数の数がサンプルの数よりも多い場合、また、説明変数同士の相関が非常に高い場合は、XTX の逆行列を計算できないケースが生じる。このとき、逆行列内の XTX にノイズを少し与えることで、逆行列を持たせるようにすることが可能である。このノイズは、パラメーター推定時に L2 ノルムを設けることで現れるようになる。
このモデルにおいてパラメーターの L2 ノルムは次のように定義される。
\[ ||\boldsymbol{\beta}||_{2}^{2} = |\beta_{1}|^{2} + |\beta_{2}|^{2} + \cdots + |\beta_{n}|^{2} \]パラメーターの最小二乗推定を行うときに、L2 ノルムを制約条件として与えた場合、次式のように書き表すことができる。
\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ ||\mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} \right\} \quad \text{subject to} \quad ||\boldsymbol{\beta}||_{2}^{2} \le t \]上記のパラメーターの推定式をラグランジュの未定乗数法を用いて書くと次のようにある。λ は正則化パラメーターとよばれ、L2 ノルムの寄与の大きさを調整する役割を果たす。パラメーター推定時に、この λ は定数として扱われる。
\[ \hat{\boldsymbol{\beta}} = \arg \min \left\{ ||\mathbf{y} - \mathbf{X}\boldsymbol{\beta}||^{2}_{2} + \lambda ||\boldsymbol{\beta}||_{2}^{2} \right\} \]これを解くために、まず λ を定数として、\( S(\boldsymbol{\beta}) = \frac{1}{2}||\mathbf{y}-\mathbf{X}\boldsymbol{\beta}||^{2}_{2} + \frac{\lambda}{2}||\boldsymbol{\beta}||_{2}^{2} \) とおいて、β に関して偏微分すればよく、I を単位行列とすると、以下のように解ける。
\[ \begin{eqnarray} && \frac{\partial S(\boldsymbol{\beta})}{\partial \boldsymbol{\beta}} = -X^{T}(\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) + \lambda\boldsymbol{\beta} = \mathbf{0} \\ &\Longrightarrow& \hat{\boldsymbol{\beta}} = (\mathbf{X}^{T}\mathbf{X} + \lambda\mathbf{I})^{-1}\mathbf{X}^{T}\mathbf{y} \end{eqnarray} \]ここまで λ を定数とみなしていた。上述の計算結果からみると、λ の値を大きくすると、逆行列内は大きな値を持つ対角行列となるので、推定量のすべての成分が 0 となるあるいは非常に小さな値をとることがわかる。逆に λ の値を小さくすると、逆行列内は XTX に近づくので、パラメーターの推定値が最小二乗推定の推定値に近づくことがわかる。この λ の値は自動的に決まらないので、Ridge 推定を行うときにあらかじめ与えておく必要がある。一般には、クロスバリデーションにより最適な λ を決めている。
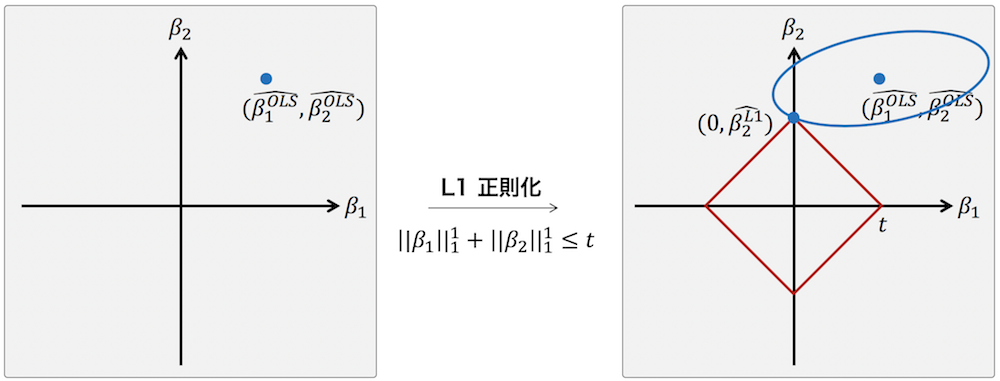
L1 ノルムを制約条件として用いる LASSO ではスパース推定が可能であるのに対して、Ridge ではスパース推定が不可能である。スパース推定が可能となるのは、パラメーター βj = 0 かつ βi≠j ≠ 0 となるような点が存在することである。具体例を示すために、2 つのパラメーター β1 および β2 のみを持つ簡単な線形回帰モデルを考える。このモデルのパラメーターを最小二乗推定により推定すると、下の右図のように β1OLS および β2OLS になったと仮定する。次に、LASSO によるパラメーター推定では、パラメーターの取りうる値は下の右図の赤枠内に制限される。そして、t の値をうまく選ぶことで、下の右図のように、β1 = 0 かつ β2 ≠ 0 となる点が見つかる。このとき、β1 = 0 と推定され、パラメーターの推定結果がスパースになる。
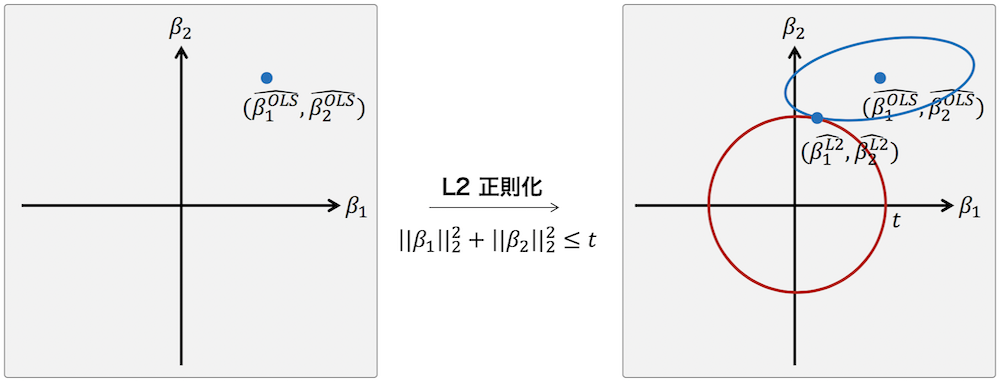
これに対して Ridge 推定では、L2 ノルムを制約条件として使っている。L2 ノルムの制約条件を図示すると次のように円となっていることがわかる。このとき、2 つの楕円(青色の楕円と赤色の円)の接点が縦軸または横軸上になるケースは非常に限られている(接線の傾きが 0 あるいは無限大になるケースは非常に限られている)。このため、Ridge によるパラメーターの推定結果はスパースにならない。
References
- Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12:55-67. DOI: 10.1080/00401706.1970.10488634