主成分分析は次元圧縮や特徴抽出などに使われている。例えば、p 次元の特徴量を持つデータに対して主成分分析を行うと、p 個の主成分が得られる。ほとんどの場合、p 個の主成分のうち最初の(寄与率の高い) 2, 3 個を取り出して、それらの主成分を散布図にプロットして、分析結果を視覚的に確認して解釈を与えるという方法で使われる。最初の 2, 3 個の主成分を選んで、それらの寄与率が大きければ、(例えば 10 個の特徴量が持つ情報量を 2 個の主成分で 8 割説明できれば、)主成分分析として解釈しやすいものとなる。しかし、各主成分の寄与率が小さいとき、(例えば 10 個の特徴量が持つ情報量を 5 個の主成分で 6 割しか説明できないよう場合であれば、)データ全体を解釈するために、より多くの主成分を選ぶ必要がある。より多くの主成分を選ぶと、その主成分の解釈が難しくなる。
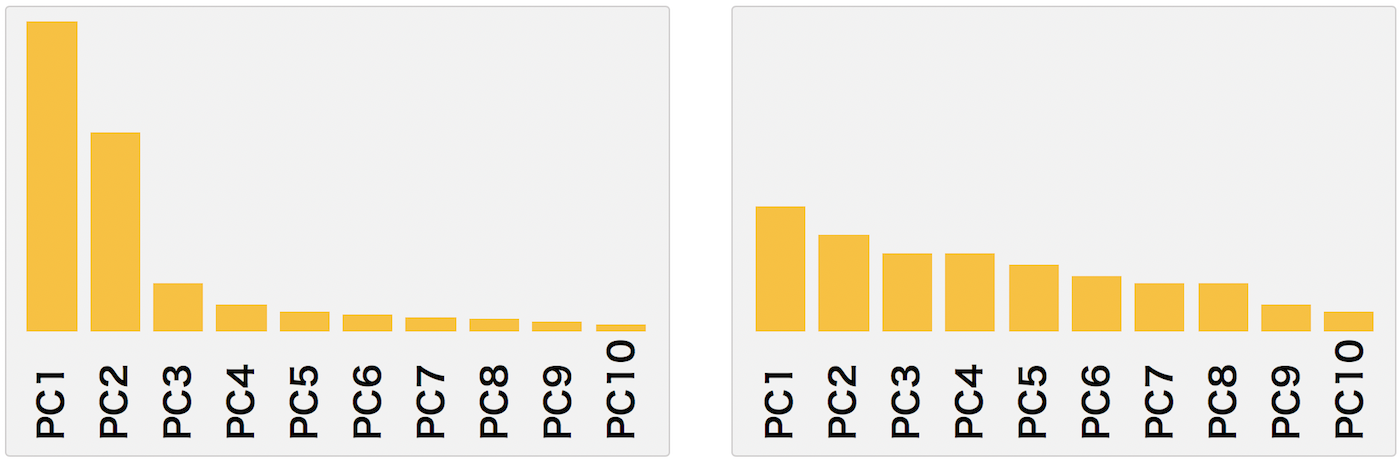
この主成分に対してもスパース推定というアプローチをすることができる。主成分を推定する際に、主成分がなるべく 0 になるように推定するアプローチである。スパース推定による主成分分析には、分散最大化による推定 SCoTLASS と二乗誤差最小化による推定 Sparse PCA などの方法がある。SCoTLASS の結果にスパース性があまり得られないことがわかっている。
α1, α2, ... を主成分分析により得られた主成分ベクトルとし、主成分ベクトルからなる行列を A = (α1, α2, ..., αn) とすると、二乗誤差最小化による主成分計算は次の式で表せる。
\[ \hat{A} = \arg \min_{A}\left\{\sum_{i=1}^{n}||\mathbf{x}_{i}-AA^{T}\mathbf{x}_{i}||^{2}_{2} \right\} \quad \text{subject to} \quad A^{T}A = I_{k} \]求められた主成分に対してスパース性を持たせたいので、各主成分ベクトルに対して正則化項を加える。λ, λ1, λ2, ..., λk > 0 を正則化パラメーターとする。
\[ \hat{A} = \arg \min_{A}\left\{\sum_{i=1}^{n}||\mathbf{x}_{i}-AA^{T}\mathbf{x}_{i}||^{2}_{2} + \lambda \sum_{j=1}^{k}||\boldsymbol{\alpha}_{j}||_{2}^{2} + \sum_{j=1}^{k}\lambda_{j}||\boldsymbol{\alpha}_{j}||_{1}^{1} \right\} \quad \text{subject to} \quad A^{T}A = I_{k} \]しかし、この式を用いて主成分分析を行うと、行列 A が直行制約と L1 正則化項を同時に満たしながら推定していくことになる。このような A を求めるのが非常に困難である。そこで、A ≓ B となる行列 B = (β1, β2, ..., βn) を考える。このとき、行列 A には直行制約を、行列 B には L1 正則化項を与えることで、計算が簡単になる。実際の計算では、行列 A と行列 B の推定を交互に繰り返すことで、両方を最小化している。
\[ \hat{A}, \hat{B} = \arg \min_{A, B}\left\{\sum_{i=1}^{n}||\mathbf{x}_{i}-AB^{T}\mathbf{x}_{i}||^{2}_{2} + \lambda \sum_{j=1}^{k}||\boldsymbol{\beta}_{j}||_{2}^{2} + \sum_{j=1}^{k}\lambda_{j}||\boldsymbol{\beta}_{j}||_{1}^{1} \right\} \quad \text{subject to} \quad A^{T}A = I_{k} \]この式に基づいたスパース推定の結果として行列 A および行列 B が得られる。行列 A は直行制約のかかった結果で、行列 B は L1 正則化項目がかかった結果となる。そのため、スパース性を持った主成分ベクトルとして、行列 B が使われる。つまり、sparse PCA によって求められた主成分ベクトルは β1, β2, ..., βk となる。ただし、行列 B は基準化されていないので、実際に k 番目の主成分は以下のように基準化されたものを利用する。
\[ \frac{\boldsymbol{\beta}_{k}}{||\boldsymbol{\beta}_{k}||_{2}} \]