2 つの確率変数の間の類似性の度合いを表す指標として相関係数がある。相関係数は -1 から +1 までの値をとり、+1 に近いときは 2 つの確率変数には正の相関があるといい、-1 に近いときは両者には負の相関があるという。相関係数は以下に示すようなものがある。
ピアソンの積率相関係数
2 セットのデータ (xi, yi) (i = 1, 2, ..., n) に対して、ピアソンの積率相関係数 rxy は次のように求められる。ただし、\(\overline{x}\) は xi (i = 1, 2, ..., n) の平均、\(\overline{y}\) は yi (i = 1, 2, ..., n) の平均である。
上式の分子は共変動とよばれ、相関の程度を表す。2 つのデータに正の相関があるときには正の値を取り、負の相関があるときには負の値を取る。相関が弱い時 0 に近い値をとる。分母は変数 x, y それぞれの標準偏差であり、共変動の絶対値を 1 以下にする役割である。そのため、相関係数は -1 以上 +1 以下の値をとる。また、分子を分母で割ることによって、相関係数は単位なしの無名数となるため、xi と yi の単位が異なっていても、相関を計算することができる。
xi (i = 1, 2, ..., n) の分散を σx2、yi (i = 1, 2, ..., n) の分散を σy2 とすると、相関係数は次のように導くこともできる。
この式の分子は、変数 x の偏差 \(x_{i} - \overline{x}\) と y の偏差 \(y_{i} - \overline{y}\) を同時に考慮していることから、共分散とよばれている。共分散は次のように計算される。
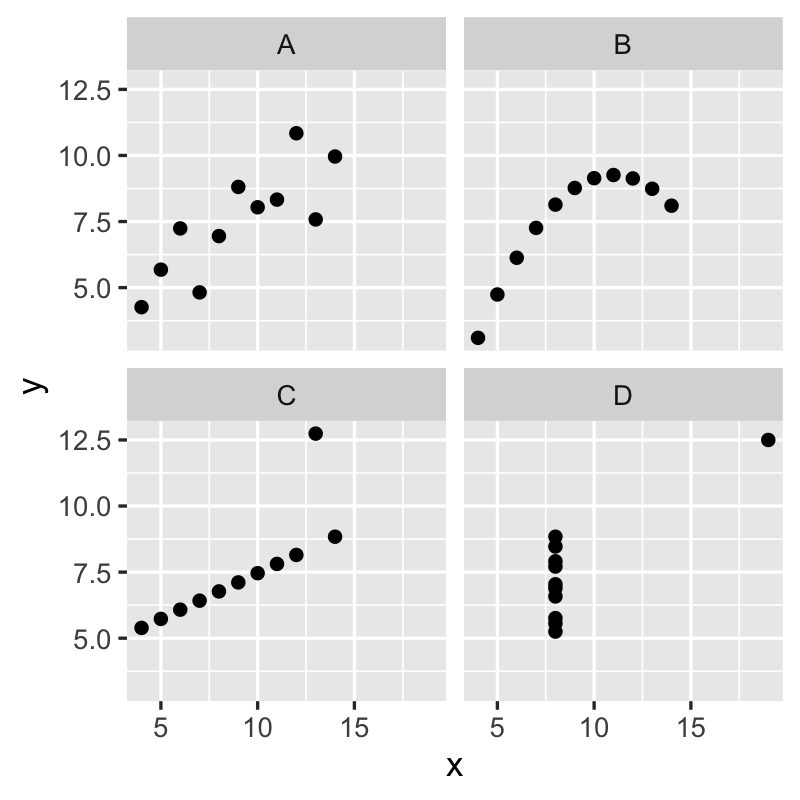
相関係数から、データの散らばり具合を正確に解釈できると限らない。相関係数の値は、データの散らばり具合やデータ中の異常値の影響を受ける。例えば下記のアンスコムの例をみると、4 つのデータセットの相関が共に 0.816 であるが、そのデータの散らばり具合が大きく異なっている。そのため、相関の程度を判断するときに、相関係数だけでなく、散布図も合わせて利用することが重要である。
R を利用してピアソンの積率相関係数を求める例。
x <- c(1.32, 2.32, 1.11, 2.42, 4.32, 2.01)
y <- c(4.61, 9.01, 3.92, 9.20, 9.86, 7.14)
cor(x, y, method = "pearson")
## [1] 0.8417847スピアマンの順位相関係数
スピアマンの順位相関係数は、値の大小関係から計算される相関係数である。2 セットのデータ (xi, yi) (i = 1, 2, ..., n) に対して、まず、その順位 (x'i, y'i) (i = 1, 2, ..., n) を求め、その順位をもとに相関係数 ρxy を計算する。ただし、di = x'i - y'i (i = 1, 2, ..., n) である。
R を利用してスピアマンの順位相関係数を求める例。
x <- c(1.32, 2.32, 1.11, 2.42, 4.32, 2.01)
y <- c(4.61, 9.01, 3.92, 9.20, 9.86, 7.14)
cor(x, y, method = "spearman")
## [1] 1ケンドールの順位相関係数
ケンドールの順位相関係数もデータの大小関係に着目して計算される相関である。ケンドールの順位相関係数の場合は、比較するペア同士の大小関係を +1 および -1 で数値化し、+1 および -1 の個数から相関を求める方法である。
(xi, yi) (i = 1, 2, ..., n) に対して、「xi>xj かつ yi>yj」または、「xi<xj かつ yi<yj」のとき +1 とする。また、「xi>xj かつ yi<yj」または、「xi<xj かつ yi>yj」のとき -1 とする。+1 を与えたペアの個数を G 個とし、-1 を与えたペアの個数を H 個とし、ケンドールの順位相関係数は次のように計算される。
\[ \tau_{xy} = \frac{G-H}{\frac{n(n-1)}{2}} \]R を利用してケンドールの順位相関係数を求める例。
x <- c(1.32, 2.32, 1.11, 2.42, 4.32, 2.01)
y <- c(4.61, 9.01, 3.92, 9.20, 9.86, 7.14)
cor(x, y, method = "kendall")
## [1] 1相関と擬似相関
相関を扱ううえで注意すべき点として、因果関係と擬似相関(見かけ上の相関)がある。2 つの変数が相関関係にあるとき、それらが必ずしも因果関係にあると限らない。例えば、アイスクリームと扇風機の売上高を調べると、両者の相関が 0.879 であった。このとき、両者は相関関係であるといえる。しかし、アイスクリームの売り上げ量の増加が原因となって、扇風機の売り上げ量を増加させたといえないので、因果関係ではない。
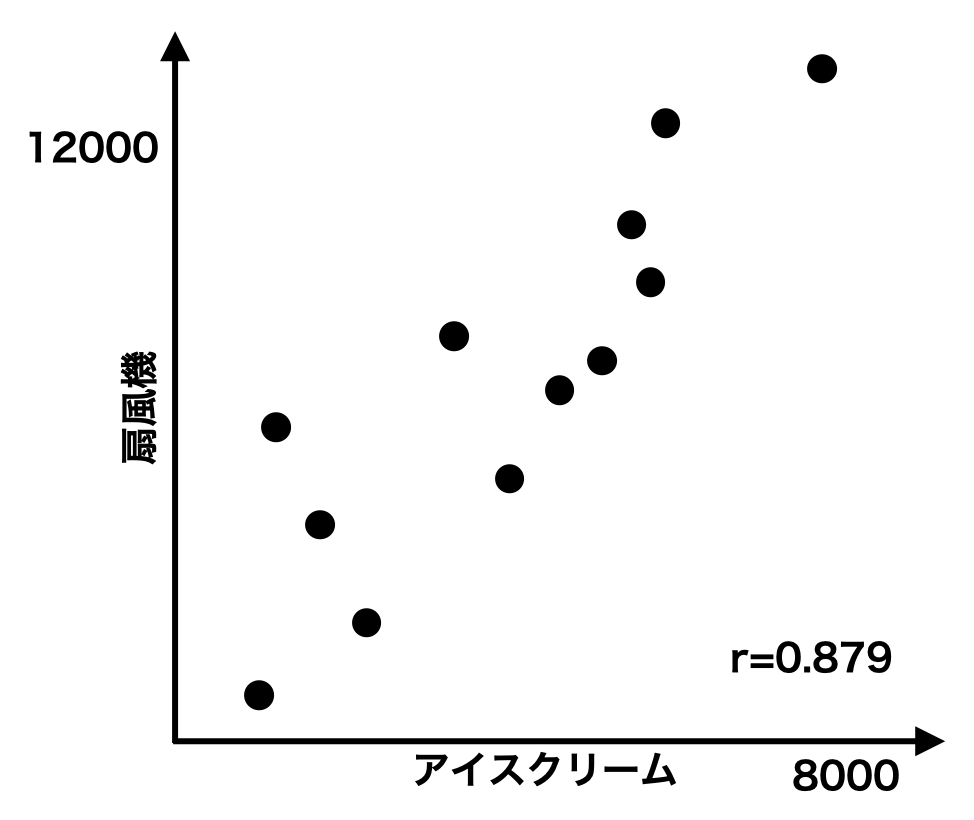
アイスクリームと扇風機の売上高を詳しく考えてみると、どちらも気温が高くなるほど売上高が増加することが考えられる。つまり、両者は見えない要因(潜伏変数)である気温に影響されていると考えられる。このように、因果関係がないのに潜伏変数の影響で相関になることを擬似相関あるいは見かけ上の相関とよぶ。
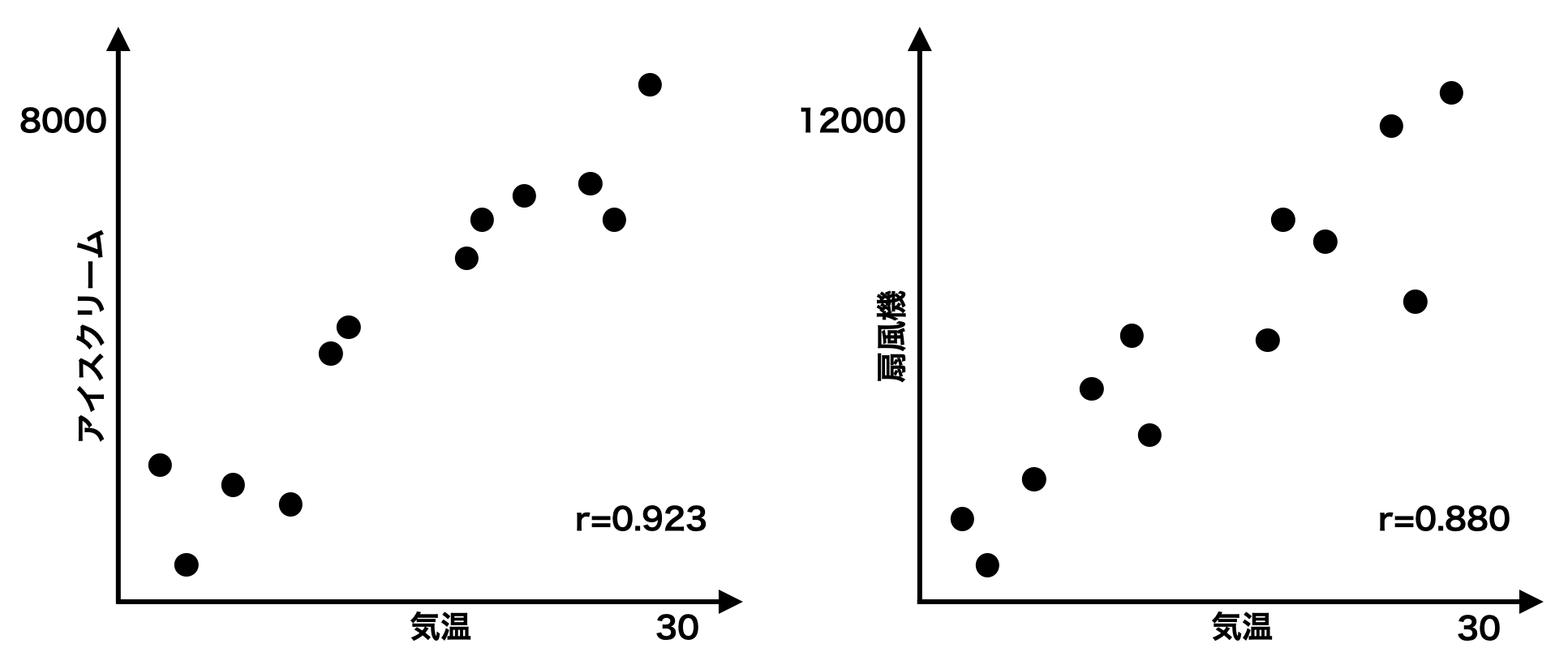
気温とアイスクリームの売上高、気温と扇風機の売上高を図示すると以下のようになる。気温の増加が、アイスクリームの売上高と扇風機の売上高を増加させたと断定できる。したがって、この場合、気温とアイスクリーム、気温と売上高は相関関係および因果関係を持つといえる。
| 気温 | 5.6 | 7.2 | 10.6 | 13.6 | 20.0 | 21.8 | 24.1 | 28.4 | 25.1 | 19.4 | 13.1 | 8.3 |
| アイスクリーム | 2285.2 | 876.9 | 1083.0 | 4302.4 | 5304.2 | 5501.9 | 5467.2 | 8402.6 | 5139.1 | 4809.9 | 4064.5 | 2052.5 |
| 扇風機 | 1752.3 | 529.3 | 6208.2 | 4365.5 | 9804.6 | 9061.3 | 9909.4 | 9804.2 | 7381.6 | 6707.3 | 8115.3 | 3704.5 |
偏相関係数
2 つの変数間に擬似相関が考えられるとき、潜伏変数を影響を取り除いた偏相関係数が用いられる。アイスクリーム売上高(変数 1)、扇風機の売上高(変数 2)から気温(変数 3)を取り除いた偏相関係数は次のように計算される。実際に、アイスクリーム売上高と扇風機の売上高の偏相関係数を計算すると 0.361 になり、たしかに相関が低いことがわかる。
\[ r_{12\cdot 3} = \frac{r_{12} - r_{13}r_{23}}{\sqrt{1-r_{13}^{2}}\sqrt{1-r_{23}^{2}}} \]