点推定と区間推定 | 正規分布における平均の点推定と区間推定

分布パラメーターの推定には点推定と区間推定というものがある。例えば、点推定は、標本データから母平均を一つの数値として推定する方法である。これに対して、区間推定は標本データから母平均が存在しうる範囲を推定する方法である。

点推定

平均や分散などを推定する際に、最尤法が使われる。ここで、正規分布の平均および分散を、最尤法による点推定を行う例を示す。

確率関数 X が平均 μ、分散 σ² の正規分布に従うとき、その確率密度関数は以下のように表すことができる。

\[ f(X; \mu, \sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\left( -\frac{(X-\mu)^{2}}{2\sigma^{2}} \right) \]

平均 μ、分散 σ² の正規分布から n 個の標本 x₁, x₂, ..., x_n を独立に抽出したとき、その同時確率関数は次のように書ける。

\[ f(x_{1},x_{2},\cdots,x_{n}; \mu, \sigma^{2}) = \left(\frac{1}{\sqrt{2\pi\sigma^{2}}}\right)^{n} \exp\left( -\sum_{i=1}^{n}\frac{(x_{i}-\mu)^{2}}{2\sigma^{2}} \right) \]

このとき、対数尤度関数は次のように計算できる。

\[ \begin{eqnarray} l(\mu, \sigma^{2}; x_{1},x_{2},\cdots,x_{n}) &=& \log L(x_{1},x_{2},\cdots,x_{n}; \mu, \sigma^{2}) \\ &=& \log f(x_{1},x_{2},\cdots,x_{n}; \mu, \sigma^{2}) \\ &=& n\log\frac{1}{\sqrt{2\pi\sigma^{2}}} - \sum_{i=1}^{n}\frac{(x_{i}-\mu)^{2}}{2\sigma^{2}} \\ &=& -\frac{n}{2}\log2\pi - \frac{n}{2}\log\sigma^{2} - \frac{1}{{2\sigma^{2}}}\sum_{i=1}^{n}(x_{i}-\mu)^{2} \end{eqnarray} \]

ここで、対数尤度関数を μ で偏微分して 0 とおくと、

\[ \frac{\partial l}{\partial \mu} = 0 \Leftrightarrow \frac{1}{{\sigma^{2}}}\left(\sum_{i=1}^{n}x_{i} - n\mu\right) = 0 \]

よって、母平均は標本平均と同じ値になる。

\[ \hat{\mu} = \overline{x} = \frac{1}{n}\sum_{i=1}^{n}x_{i} \]

次に、対数尤度関数を σ² で偏微分して 0 とおくと、σ² は次のように求められる。

\[ \begin{eqnarray} \frac{\partial l}{\partial \sigma^{2}} = 0 &\Leftrightarrow& -\frac{n}{2\sigma^{2}} + \frac{1}{{2\sigma^{4}}}\sum_{i=1}^{n}(x_{i}-\mu)^{2} = 0 \\ &\Leftrightarrow& \frac{1}{{2\sigma^{4}}}\sum_{i=1}^{n}(x_{i}-\mu)^{2} = \frac{n}{2\sigma^{2}} \\ \end{eqnarray} \]

よって、母分散は次のように推定される。

\[ \hat{\sigma}^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i}-\mu)^{2} = \frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})^{2} \]

実際には、対数尤度関数が \( \mu = \hat{\mu} \) および \(\sigma^{2} = \hat{\sigma}^{2}\) において最大値を取ることも証明する必要がある。また、ここで推定されている母分散は、不偏分散と異なることに注意すること。

区間推定

サンプルサイズが大きい場合

中心極限定理により、母集団が平均 μ および分散 σ の分布であるとき、母集団から抽出された標本の平均は、平均 μ および分散 σ²/n の正規分布に従うことが知られている。

\[ \overline{x} \sim \mathcal{N}(\mu, \frac{\sigma^{2}}{n}) \]

書き換えると（標準化すると）、

\[ z_{n} = \frac{(\overline{x} - \mu)}{\frac{\sigma}{\sqrt{n}}} \sim \mathcal{N}(0, 1) \]

ここで、標準正規分布において、確率変数 z が z_α/2 よりも大きくなる確率は α/2 とする。また、確率変数 z が z_-α/2 よりも大きくなる確率は α/2 とする。

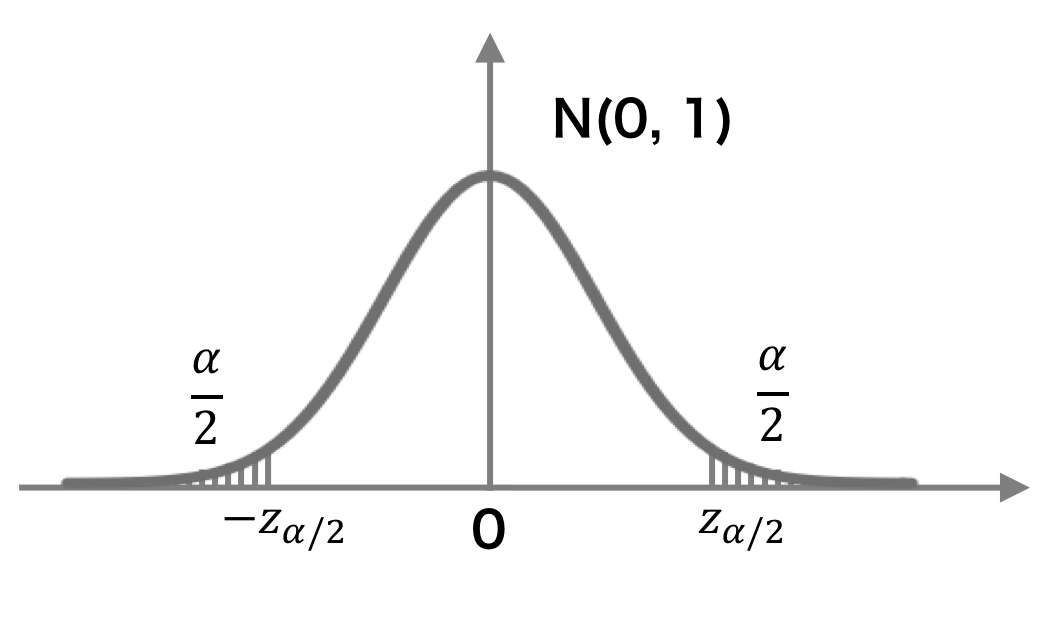
このとき、z_n は 1-α の確率で次の範囲の値を取ることがわかる。

\[ P\left( -z_{\alpha/2} \le z_{n} \le z_{\alpha/2} \right) = 1 - \alpha \]

よって、母平均は 1-α の確率で次の範囲の値を取ることがわかる。

\[ P\left( -z_{\alpha/2} \le \frac{(\overline{x} - \mu)}{\frac{\sigma}{\sqrt{n}}} \le z_{\alpha/2} \right) = 1 - \alpha \]

これより、

\[ P\left( \overline{x} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \le \mu \le \overline{x} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}} \right) = 1 - \alpha \]

例えば 0.95 の確率で母平均は次の範囲にあることが推定される。z_0.05/2 = 1.96 により、

\[ P\left( \overline{x} - 1.96\frac{\sigma}{\sqrt{n}} \le \mu \le \overline{x} + 1.96\frac{\sigma}{\sqrt{n}} \right) = 0.95 \]

また、母分散 σ² が未知のとき、母分散を標本不偏分散 s² で代用する。

\[ P\left( \overline{x} - z_{\alpha/2}\frac{s}{\sqrt{n}} \le \mu \le \overline{x} + z_{\alpha/2}\frac{s}{\sqrt{n}} \right) = 1 - \alpha \] \[ s^{2} = \frac{1}{n-1} \sum_{i=1}^{n}(x_{i} - \overline{x})^{2} \]

サンプルサイズが小さい場合

サンプルサイズが小さいとき、母分散 σ² を標本不偏分散 s² に置き換えると、z_n は自由度 n - 1 の t 分布に従うことが W.S. Gosset および R.A. Fisher によって示されている。すなわち、

\[ z_{n} = \frac{(\overline{x} - \mu)}{\frac{s}{\sqrt{n}}} \sim \mathcal{t}(n - 1) \]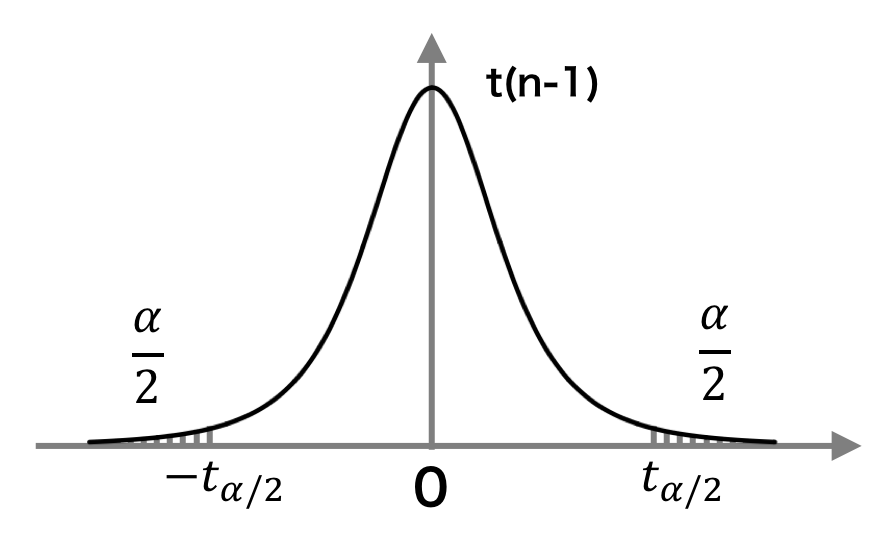

これにより、サンプルサイズが小さいときの、母平均の区間推定は次のように推定される。

\[ P\left( \overline{x} - t_{\alpha/2}\frac{s}{\sqrt{n}} \le \mu \le \overline{x} + t_{\alpha/2}\frac{s}{\sqrt{n}} \right) = 1 - \alpha \] \[ s^{2} = \frac{1}{n-1} \sum_{i=1}^{n}(x_{i} - \overline{x})^{2} \]