密度推定

y = ax + b のような回帰を locfit 関数で推定する例を示す。まず、乱数でデータを生成する。

x <- runif(100, 0, 100)
y <- rnorm(100 , 10, 3) * x + rnorm(100, 5, 2)  # y = 10x + 5
dat <- data.frame(y = y, x = x)

locfit で密度推定を行う。

fit <- locfit(y ~ x, data = dat)

推定した密度をグラフ上に示す。

plot(dat$x, dat$y, pch = 19, cex = 0.8, col = "grey")

# 回帰曲線
fit.fun <- function(x) predict(fit, data.frame(x = x))
curve(fit.fun, add = TRUE, col = "orange", lwd = 2)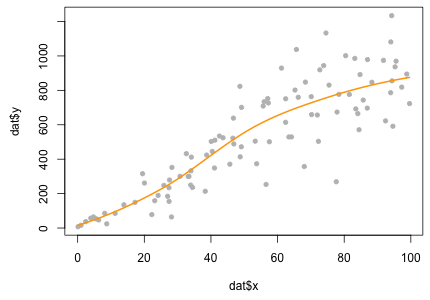

局所回帰（負の二項分布における平均とばらつきの関係について）

RNA-seq を利用したトランスクリプトーム解析ではリードのカウントデータを利用してモデル構築を行う場合がある。この際に、カウントデータを負の二項分布に従うもとして、平均とばらつきの関係を求めるステップがある。

まず、RNA-seq のリードカウントデータから平均およびばらつきを求める。サンプルデータは A 群と B 群からなるが、ここでは A 群のデータのみを利用する。本来は平均と分散を求める際に正規化を行う必要はあるが、ここでは locfit の使い方に着目しているので、正規化の作業を略する。

counts <- read.table("https://stats.biopapyrus.jp/data/counts_3_3.txt", header = TRUE)
counts <- counts[, 2:4]

bm <- apply(counts, 1, mean)
bv <- apply(counts, 1, var)

dat <- data.frame(logMean = log(bm), logDisp = log((bv - bm) / bm^2))
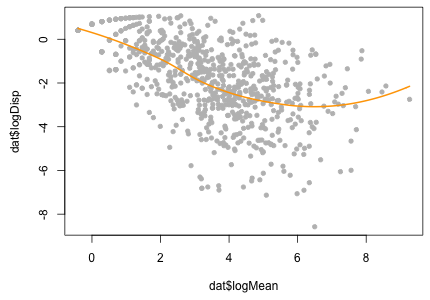
dat <- dat[!(is.na(dat[, 2]) | is.infinite(dat[, 2])), ]

次に、locfit 関数を利用して、平均とばらつきの回帰曲線を予測する。

fit <- locfit(logDisp ~ logMean, data = dat)

予測結果をグラフに示す。

# 観測データ
plot(dat$logMean, dat$logDisp, pch = 19, cex = 0.8, col = "grey")

# 回帰曲線
fit.fun <- function(x) predict(fit, data.frame(logMean = x))
curve(fit.fun, add = TRUE, col = "orange", lwd = 2)