主成分分析(PCA)は、多次元のデータをより少次元に置き換える、次元縮約の方法の一つである。多次元のデータに対して、分散が最も大きくなるような次元を探し当てれば、その次元だけで、データが持つ情報の多くを説明できるようになる。PCA はそのような分散が最も大きくなるような次元(主成分)を探す方法である。
主成分の計算
n 個のサンプルのそれぞれに対して、p 項目の調査データ(特徴)があると仮定したとき、データ全体は n × p の行列で表せる。ここで、i (1 ≤ i ≤ p) 番目の特徴を \(\mathbf{x}_{i} = (x_{1i}, x_{2i}, \cdots, x_{ni})^{T} \) で表し、全サンプルのデータからなる n × p の行列をベクトル表示で \(\mathbf{X} = (\mathbf{x}_{1}, \mathbf{x}_{2}, \cdots, \mathbf{x}_{n})\) と表す。
分散共分散行列
次に、p 個の特徴(調査項目)のうち、k 番目と l 番目の特徴の共分散は、定義式に従って、次のように計算することができる。
\[ \begin{eqnarray} Cov(\mathbf{x}_{k}, \mathbf{x}_{l}) &=& E\left[\left(\mathbf{x}_{k}-E[\mathbf{x}_{k}]\right)\left(\mathbf{x}_{l}-E[\mathbf{x}_{l}]\right)\right] \\ &=& \frac{1}{n}\sum_{j=1}^{n}\left( x_{jk} - \mu_{k} \right) \left( x_{jl} - \mu_{l} \right) \\ &=& \frac{1}{n}\mathbf{x'}_{k}^{T}\mathbf{x'}_{l} \end{eqnarray} \]ただし、\( \mu_{k} = \sum_{j=1}^{n}x_{jk} \) とし、また、\( \mathbf{x'}_{k} = (x_{1k}-\mu_{k}, x_{2k}-\mu_{k}, \cdots, x_{nk}-\mu_{k})^{T} \) とした。
p 個の特徴に対して、特徴のペア同士の共分散を、すべての組み合わせに対して計算すると、次のような分散共分散行列 Σ が得られる。
\[ \mathbf{\Sigma}_{\mathbf{X}} = \begin{bmatrix} Cov(\mathbf{x}_{1}, \mathbf{x}_{1}) & Cov(\mathbf{x}_{1}, \mathbf{x}_{2}) & \cdots & Cov(\mathbf{x}_{1}, \mathbf{x}_{n}) \\ Cov(\mathbf{x}_{2}, \mathbf{x}_{1}) & Cov(\mathbf{x}_{2}, \mathbf{x}_{2}) & \cdots & Cov(\mathbf{x}_{2}, \mathbf{x}_{n}) \\ \vdots & \vdots & \ddots & \vdots \\ Cov(\mathbf{x}_{n}, \mathbf{x}_{1}) & Cov(\mathbf{x}_{n}, \mathbf{x}_{2}) & \cdots & Cov(\mathbf{x}_{n}, \mathbf{x}_{n}) \end{bmatrix} = \frac{1}{n}\mathbf{X'}^{T}\mathbf{X'} \]
ただし、\(\mathbf{X'} = (\mathbf{x'}_{1}, \mathbf{x'}_{2}, \cdots, \mathbf{x'}_{n} )\) とした。
固有値問題への帰着
PCA の目標は、特徴の分散が最大となるような次元を見つけることである。そのため、既存のデータ \(\mathbf{X}\) に対して座標変換を行い、変換後のデータの分散が最大となるような変換を見つければよい。ここで、\(\mathbf{X}\) に対して、座標変換を行うために、ある射影ベクトル \( \mathbf{w} \) をかけて、新しい座標を \(\mathbf{z}\) を計算する。このとき、n 次元であったサンプルの特徴量が射影ベクトル \( \mathbf{w} \) によって 1 つの点に置換されることに注意。
\[ \mathbf{z} = \mathbf{X}\mathbf{w} \]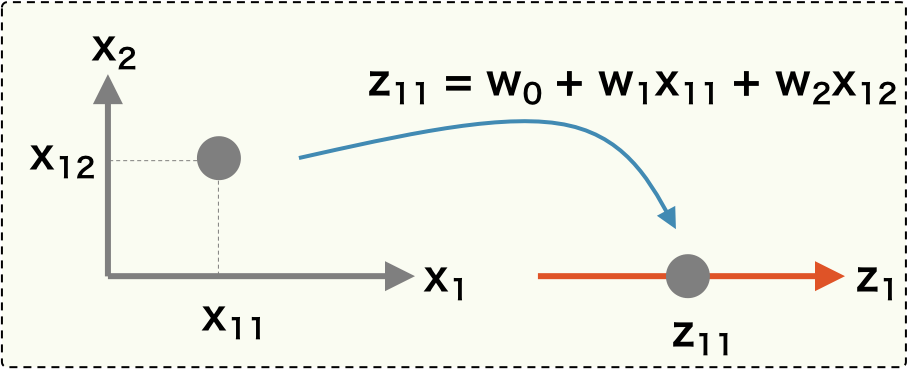
こうして得られた変換後の新しい座標 \(\mathbf{z} = (z_{1}, z_{2}, \cdots, z_{n})\) の分散を最大にするベクトル \(\mathbf{w}\) を求めればよい。そのために、\(\mathbf{z}\) の分散を計算する必要がある。上と同様にして、\(\mathbf{z}\) の分散は次のように計算できる。
\[ \mathbf{\Sigma}_{\mathbf{z}} = \frac{1}{n}\mathbf{z'}^{T}\mathbf{z'} \]\( \mathbf{z} = \mathbf{X}\mathbf{w} \) だから、\(\mathbf{z}\) の分散は、\(\mathbf{X}\) の分散共分散行列を使って次のように置き換えることができる。
\[ \begin{eqnarray} \mathbf{\Sigma}_{\mathbf{z}} = \frac{1}{n}\mathbf{z'}^{T}\mathbf{z'} &=& \frac{1}{n}(\mathbf{X'}\mathbf{w})^{T}(\mathbf{X'}\mathbf{w}) \\ &=& \frac{1}{n}\mathbf{w}^{T}\mathbf{X'}^{T}\mathbf{X'}\mathbf{w} \\ &=& \mathbf{w}^{T}\mathbf{\Sigma}_{\mathbf{X}}\mathbf{w} \end{eqnarray} \]変換後のデータの分散を最大にしたいので、\(\mathbf{\Sigma}_{\mathbf{z}}\) となるようなベクトル \(\mathbf{w}\) を求めればよい。ベクトル \(\mathbf{w}\) は単位ベクトルなので、 \(||\mathbf{w}|| = 1\) という制約を利用すれば、ラグランジェの未定乗数法で \(\mathbf{w}\) を解くことができる。
\[ L(\mathbf{w}) = \mathbf{w}^{T}\mathbf{\Sigma}\mathbf{w} - \lambda (\mathbf{w}^{T}\mathbf{w} - 1) \]この式を最大化する \(\mathbf{w}\) は、関数 L を \(\mathbf{w}\) で偏微分した一次導関数を 0 と置くことで計算される。
\[ \frac{\partial L(\mathbf{w})}{\partial \mathbf{w}} = 2 \mathbf{\Sigma}\mathbf{w} - 2 \lambda \mathbf{w} = 0 \] \[ \Sigma_{\mathbf{X'}}\mathbf{w} = \lambda\mathbf{w} \]このように PCA は固有値問題へと導かれる。データ \(\mathbf{X}\) が p 個の特徴量を持つとき、\( \Sigma_{\mathbf{X'}} \) は p×p の行列となるので、p 個の固有値が求まる。これら p 個の固有値を降順にならべて、λ1 > λ2 > λ3 > ... > λp とする。次に、それぞれの固有値 λi に対して固有ベクトル \(\mathbf{w}_{j}\) を求める。
主成分得点
p 個の固有値および固有ベクトルが求まると、行列 \(\mathbf{X}\) を回転させたあとの座標も計算できるようになる。例えば、k 番目の固有ベクトルを用いると、次のような回転後の座標が得られる。これを、第 k 主成分の主成分得点(主成分スコア)という。
\[ \mathbf{z}_{k} = \mathbf{X}\mathbf{w}_{k} \]主成分分析は、p 次元のデータを低次元に射影する次元削減に使われている。そのため、p 次元のデータを、第 1 主成分および第 2 主成分からなる二次元平面上にプロットしたり、あるいは第 3 主成分も含めて立体図にプロットしたりしてデータの分布状況を確認することが行われている。
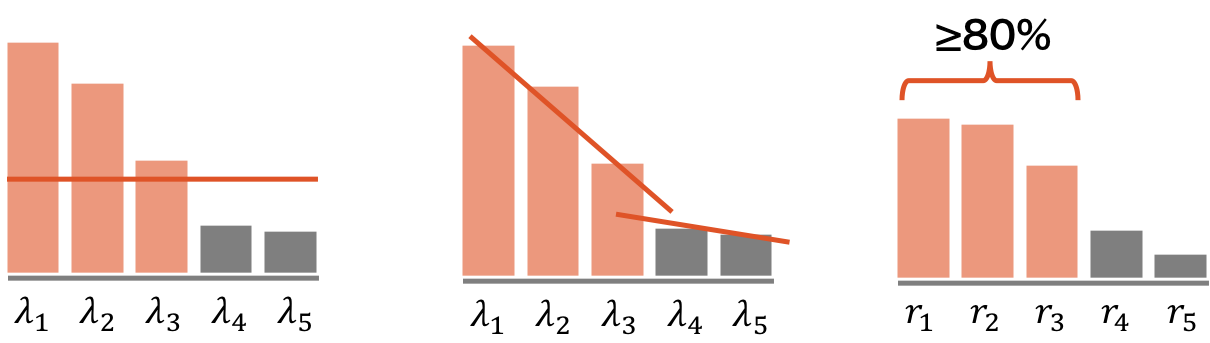
p 次元のデータを何次元に射影するか(主成分をいくつ選ぶか)は、研究分野や目的によって異なる。統計などであれば、例えば、ある閾値以上の分散(固有値)を持つ主成分を選ぶ、固有値の下がり具合が穏やかになったところまでの主成分を選ぶ、あるいは累積寄与率が 80-90% に達するまでの主成分を選ぶ、などの選び方がある。また、機械学習であれば、クロスバリデーションなどにより、最適な個数を見積もることもできる。
寄与率
第 k 主成分軸におけるデータの分散を計算すると、次のように λk として求まる。つまり、第 k 主成分軸におけるデータの分散は、k 番目に大きい固有値に等しい。
\[ \Sigma_{\mathbf{z}_{k}} = \mathbf{w}^{T}_{k}\Sigma_{\mathbf{X}}\mathbf{w}_{k} = \mathbf{w}^{T}_{k}\lambda_{k}\mathbf{w}_{k} = \lambda_{k}\mathbf{w}^{T}_{k}\mathbf{w}_{k}=\lambda_{k} \]各主成分の寄与率は、その主成分がデータが持つ全情報量のうち、どれぐらいの割合を説明できるのかを示している割合である。この寄与率は、次のように計算される。
\[ \frac{\lambda_{k}}{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{p}} \]また、第 1 主成分から第 k 主成分までの主成分を用いて説明できるデータの全情報量の割合を累積寄与率といい、次のように計算される。
\[ \frac{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{k}}{\lambda_{1} + \lambda_{2} + \cdots + \lambda_{p}} \]主成分負荷量(因子負荷量)
観測データの各特徴量と各主成分の相関を主成分負荷量(因子負荷量)という。例えば、観測データの j 番目の特徴量と第 k 主成分の主成分負荷量は、次のようにして計算できる。
\[ Cov(x^{'}_{j}, z^{'}_{k}) = \frac{\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\bar{x}) (y_{i}-\bar{y})} {\sqrt{\frac{1}{n} \sum_{i=1}^{n}(x_{i}-\bar{x})^{2}} \sqrt{\frac{1}{n} \sum_{i=1}^{n}(y_{i}-\bar{y})^{2}}} \]bioplot をプロットしたとき、上で計算した相関係数を 10 倍した値が赤の矢印として描かれる。
R による PCA
R には 2 つの PCA を行う関数 prcomp と princomp がある。2 つの関数の入力パラメーターと出力フォーマットが異なるが、実際の解析ではともに PCA を行なう。
各特徴の単位が揃っているときは、データをそのまま PCA 行うことができる。しかし、各特徴の単位が揃っていないとき(cm だったり、g だったり)、各特徴を正規化(標準化)しておく必要がある。標準化を行う場合、prcomp 関数では scale = TRUE を指定し、princomp 関数では cor = TRUE を指定する。各関数の実行例を次に示す。(このデータはフィッシャーのアヤメのデータであり、測定単位はすべて cm となっているため、本来は正規化する必要はない。)
data(iris)
iris.data <- iris[, 1:4]
iris.name <- iris[, 5]
p1 <- prcomp(iris.data, scale = TRUE)
summary(p1)
## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.7084 0.9560 0.38309 0.14393
## Proportion of Variance 0.7296 0.2285 0.03669 0.00518
## Cumulative Proportion 0.7296 0.9581 0.99482 1.00000
p2 <- prcomp(iris.data, scale = FALSE)
summary(p2)
## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 2.0563 0.49262 0.2797 0.15439
## Proportion of Variance 0.9246 0.05307 0.0171 0.00521
## Cumulative Proportion 0.9246 0.97769 0.9948 1.00000
p3 <- princomp(iris.data, cor = TRUE)
summary(p3)
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4
## Standard deviation 1.7083611 0.9560494 0.38308860 0.143926497
## Proportion of Variance 0.7296245 0.2285076 0.03668922 0.005178709
## Cumulative Proportion 0.7296245 0.9581321 0.99482129 1.000000000
p4 <- princomp(iris.data, cor = FALSE)
summary(p4)
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4
## Standard deviation 2.0494032 0.49097143 0.27872586 0.153870700
## Proportion of Variance 0.9246187 0.05306648 0.01710261 0.005212184
## Cumulative Proportion 0.9246187 0.97768521 0.99478782 1.000000000prcomp
prcomp 関数の出力結果には標準偏差 sdev、固有ベクトル rotation、特徴量平均値 center、正規化パラメーター scale、主成分スコア x が保存されている。
data(iris)
iris.data <- iris[, 1:4]
iris.name <- iris[, 5]
p <- prcomp(iris.data, scale = TRUE)
names(p)
## [1] "sdev" "rotation" "center" "scale" "x"
head(p$x)
## PC1 PC2 PC3 PC4
## [1,] -2.684126 -0.3193972 0.02791483 0.002262437
## [2,] -2.714142 0.1770012 0.21046427 0.099026550
## [3,] -2.888991 0.1449494 -0.01790026 0.019968390
## [4,] -2.745343 0.3182990 -0.03155937 -0.075575817
## [5,] -2.728717 -0.3267545 -0.09007924 -0.061258593
## [6,] -2.280860 -0.7413304 -0.16867766 -0.024200858
biplot(p)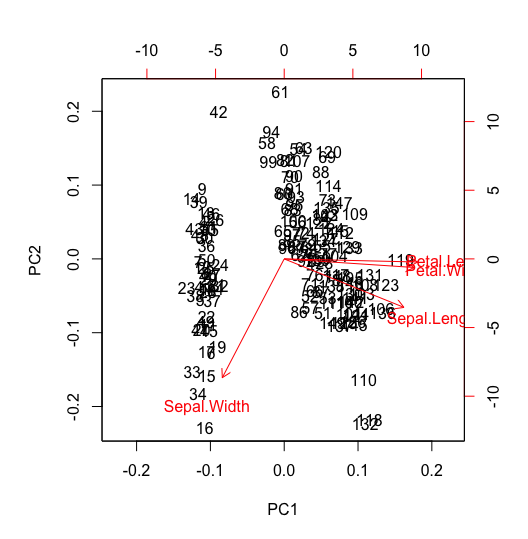
biplot プロットの横軸(下)と縦軸(左)がそれぞれ第 1 主成分と第 2 主成分の軸であり、その値が主成分得点である。各データの主成分得点は、ラベルでプロットされている。また、赤の矢印は主成分負荷量を 10 倍した値を示し、横軸(上)と縦軸(右)が目盛りである。
# red arrow for Sepal.Length at PC1 and PC2
cor(scale(d[, 1]), scale(obj$x[, 1]))
# 0.8901688
cor(scale(d[, 1]), scale(obj$x[, 2]))
# -0.3208299princomp
princomp 関数の出力結果には標準偏差 sdev、固有ベクトル loadings、特徴量平均値 center、正規化パラメーター scale、サンプル数 n.obs、主成分スコア scores、関数実行コマンドログ call が保存されている。
data(iris)
iris.data <- iris[, 1:4]
iris.name <- iris[, 5]
p <- princomp(iris.data, cor = TRUE)
names(p)
## [1] "sdev" "loadings" "center" "scale" "n.obs" "scores" "call"
head(p$scores)
## Comp.1 Comp.2 Comp.3 Comp.4
## [1,] -2.684126 0.3193972 0.02791483 0.002262437
## [2,] -2.714142 -0.1770012 0.21046427 0.099026550
## [3,] -2.888991 -0.1449494 -0.01790026 0.019968390
## [4,] -2.745343 -0.3182990 -0.03155937 -0.075575817
## [5,] -2.728717 0.3267545 -0.09007924 -0.061258593
## [6,] -2.280860 0.7413304 -0.16867766 -0.024200858