データを何らかの確率分布に従うと仮定して解析を行うとき、その確率分布の形を決めるためのパラメーター(母数)が存在する。例えば、生まれてからずっと A 餌を与えたマウスの 30 日目の体重データを、正規分布に従うと仮定して解析を行うケースを考えてみる。正規分布の形を決めるためのパラメーターは平均と分散の 2 つがある。マウス体重データから平均と分散を推定することができれば、A 餌の効果を解明できるかもしれない。ここで仮に 1 万匹のマウスに対してこのような実験を行ったとする。そして、この 1 万匹のマウスすべてに対して体重を測れば、正確な平均と分散を計算できる。しかし、この実験にはコストがかかり非現実である。これに対して、この 1 万匹のマウスの中から無作為に 3 匹のマウスを取り出して、体重を測って、平均と分散を求めることがそれほどコストがかからない。この無作為に取り出したマウスのことを標本といい、標本から計算される平均と分散をそれぞれ標本平均と標本分散という。これに対して、抽出元の集団を母集団といい、母集団の平均および分散を母平均、母分散という。一定の仮定をおけば、標本平均と標本分散から母平均と母分散を統計的に推定できる。言い換えると、一定の仮定をおけば、わざわざ 1 万匹のマウスに対して実験を行わなくても、3 匹のマウスに対して実験を行うだけで、1 万匹のマウスの分布パラメーター(平均と分散)を推定できるようになる。
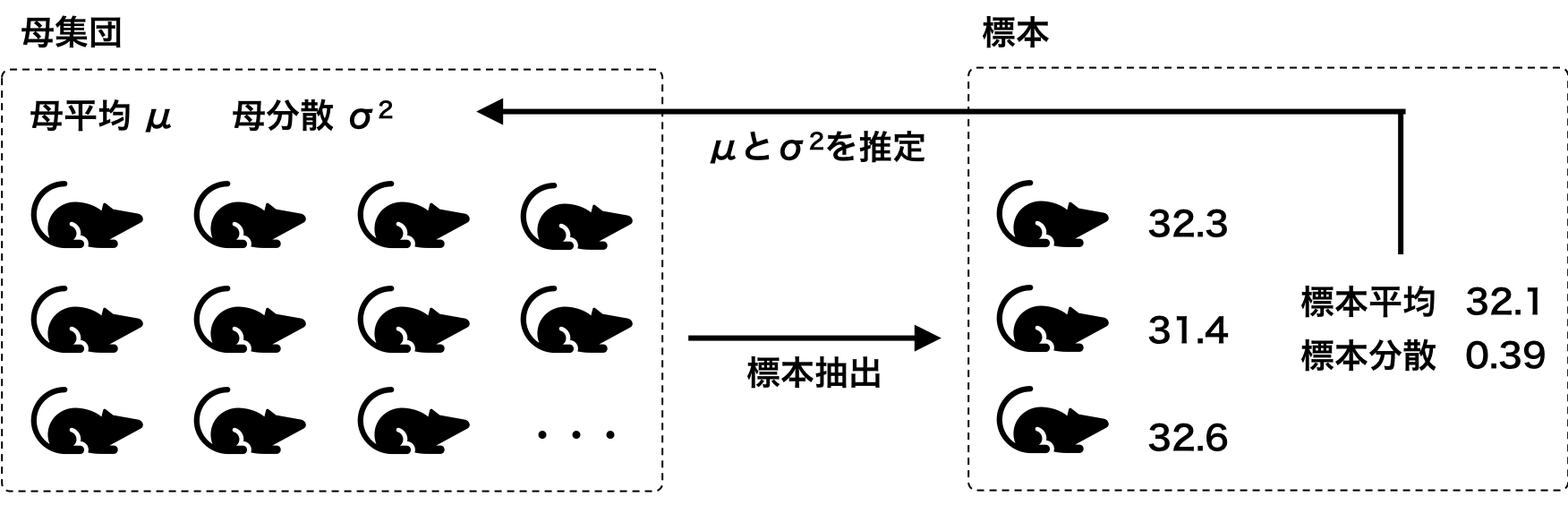
現実では、母集団は実在していない場合が多い。例えば、A 餌の効果を調べるために、地球上に存在するすべての生まれたばかりのマウスを集めて実験すれば良いが、それは非現実的である。マウスは絶え間なく、毎日繁殖しているわけで、すべてのマウスを集め続けるというのは現実的ではない。そこで、生物学実験では、「生まれてからずっと A 餌を与えたマウスの 30 日目の体重」は平均 μ および分散 σ2 の正規分布に従うことを仮定している。そして、同じ条件下で同じ方法で実験すれば、誰がどこで実験しても、この仮定された母集団(平均 μ および分散 σ2 の正規分布)から標本を取り出しているのに等しい。
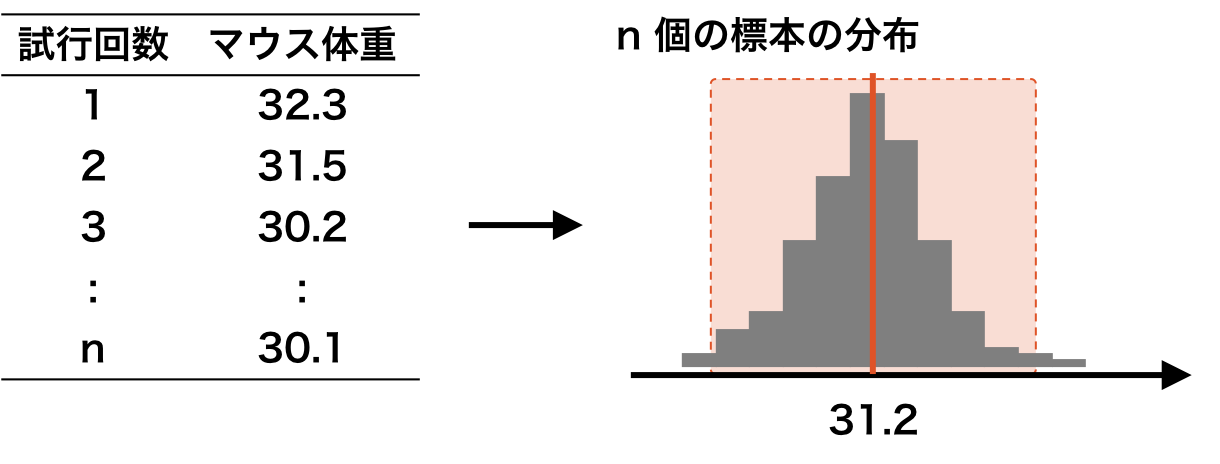
「生まれてからずっと A 餌を与えたマウスの 30 日目の体重」を測定する実験を n 回独立に行ってみる。言い換えれば、母集団から標本を抽出する試行を独立に n 回行う。n を限りなく大きくすれば、標本の数は、母集団の数に近づく。つまり、n 個の標本から計算される平均が、母集団の平均に近づく(大数の法則)。
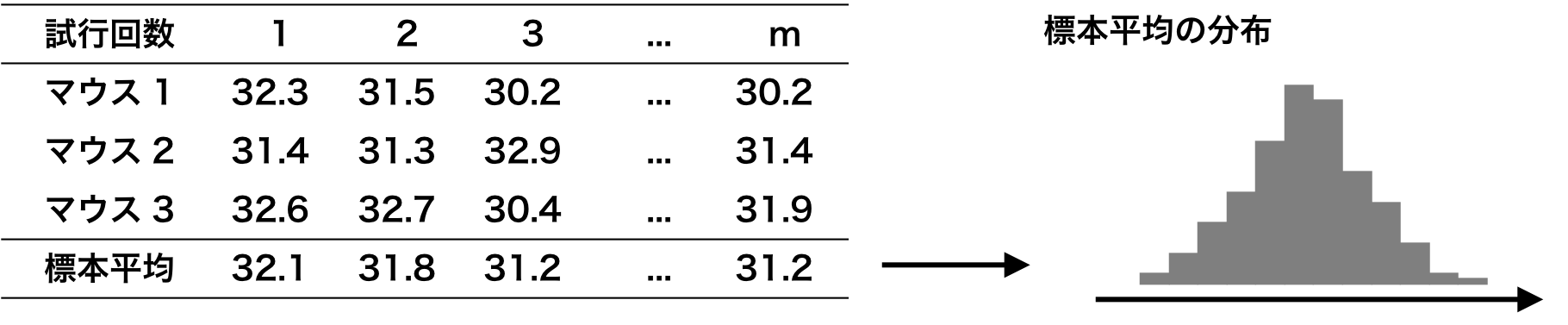
母集団が平均 μ および分散 σ の分布であるとき、母集団から抽出された標本の平均は、平均 μ および分散 σ2/n の正規分布に従うことが知られている(中心極限定理)。例えば、「生まれてからずっと A 餌を与えたマウスの 30 日目の体重」を測定する実験を 3 匹のマウスに対して行なったとき、3 つのマウスから標本平均を計算することができる。このような試行(3 匹のマウスの体重を測る試行)を独立に m 回行なったとき、m 個の標本平均を求めることができる。この m 個の標本平均の分布を調べると、標本平均の分布は、平均 μ および分散 σ2/n の正規分布に従うことが知られている。
これらの定理を利用して、標本平均から母平均を推定することを点推定という。また、母平均を 1 つの値として推定するのではなく、母平均が取りうる値の範囲を推定することを区間推定という。