t 検定 | 2 つの母集団の平均の有意差を検定

t 検定は、標本データから t 値とよばれる統計量を計算し、t 値を利用して 2 つのグループ間の母平均に差があるかどうかを検定する方法である。

X₁, X₂, ..., X_n を、平均 μ および分散 σ² の正規分布に従う確率変数とする。このとき、t 値は、標本平均を \(\overline{X}\) および標本不偏分散を \(S^{2}\) を用いて次のようにかける。サンプルサイズ n が小さいとき、t は自由度 n - 1 の t 分布に従う。

\[ t = \frac{(\overline{x} - \mu)}{\frac{S}{\sqrt{n}}} \sim t(n-1) \]

これにより、t 分布を利用して、母平均の信頼区間を求めることができる。例えば、サンプルサイズが大きい時の母平均の区間推定と同様な手順で、小サンプルサイズの場合、母平均は確率 α で次の範囲内に収まる。

\[ P\left( \overline{x} - t_{\alpha/2}\frac{s}{\sqrt{n}} \le \mu \le \overline{x} + t_{\alpha/2}\frac{s}{\sqrt{n}} \right) = 1 - \alpha \] \[ s^{2} = \frac{1}{n-1} \sum_{i=1}^{n}(x_{i} - \overline{x})^{2} \]

このことを利用して、標本平均と母平均の差を検定したり、2 つのグループ間の母平均の差を検定したりすることができるようになる。

1 標本 t 検定

帰無仮説

ある母集団から n 個の標本 X₁, X₂, ..., X_n を独立に抽出したとき、n 個の標本を使って、その母集団の平均が μ であるかどうかを検定する方法である。ここで、検定を行うために、帰無仮説 H₀ を「標本平均 \(\overline{X}\) は母平均 \(\mu\) と等しい」とする。

\[ H_{0}: \overline{X} = \mu \]

仮説を \( \overline{X} = \mu \) とする理由は、この仮説が起こりうるケースがただ 1 通りしかないからである。例えば、\( \overline{X} \ne \mu \) を仮説としたとき、\( \overline{X} > \mu \) も成り立つし、\( \overline{X} < \mu \) も成り立つ、さらに \( \overline{X} < 2\mu \)、\( \overline{X} < 3\mu \) のようなケースも考えられる。そのため、\( \overline{X} \ne \mu \) を仮説としたとき、様々なケースについて検証していく必要がある。これ対して、仮説を \( \overline{X} = \mu \) とすれば、\( \overline{X} = \mu \) というケースだけを検証していけば必要十分である。

ここで、サンプルサイズが小さいとき、帰無仮説 H₀ が正しければ、T 値は自由度 ν = n - 1 の t 分布に従う。

\[ T = \frac{(\overline{X} - \mu)}{\frac{S}{\sqrt{n}}} \sim t(n-1) \]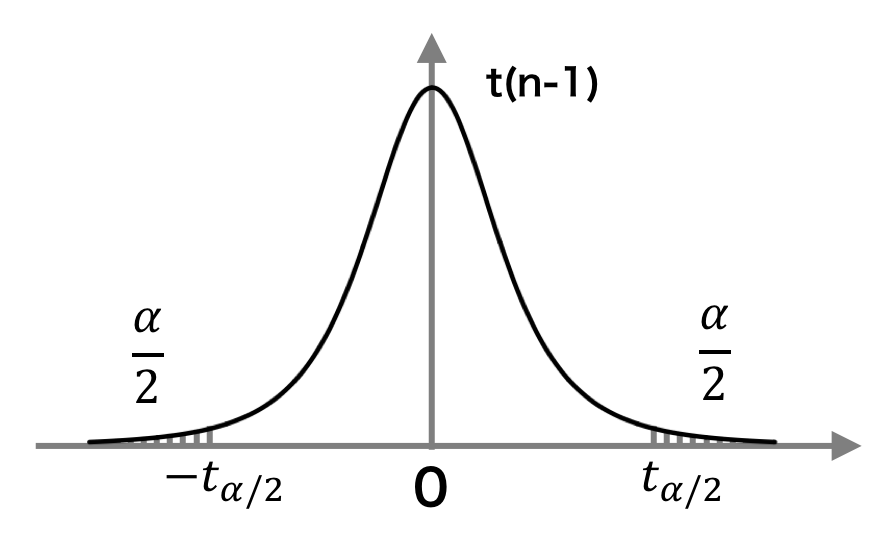

検定と危険率

t 分布の形から、T 値は 0 の値になる確率が最も高く、また、±∞ になる確率も 0 ではないことがわかる。ここで、T ≤ -t_α/2 のときの確率が α/2、T ≥ t_α/2 のときの確率が α/2 となるような点 t_α/2 および点 -t_α/2 に着目してみる。このとき、帰無仮説が正しければ、つまり標本平均が μ と同値であれば、標本データから計算される T の値は確率 1 - α で -t_α/2 < T < t_α/2 の範囲に収まる。例えば α = 0.05 のとき、T 値は 0.95 の確率で -t_0.025 < T < t_0.025 に収まる。もちろん、-t_0.025 < T < t_0.025 以外の値も取りうるが、その確率は 0.05 であり、極めて小さい。

そこで、T 値は確率 1 - α で -t_α/2 < T < t_α/2 の範囲に収まるから、T の値がこの範囲にあるとき帰無仮説を保留して、T の値がこの範囲の外側にあるとき帰無仮説を棄却して（つまり標本平均が μ と同値ではないと判断して）、バッサリ判定を下すことができる。このとき、T の値は確率 α で -t_α/2 < T < t_α/2 の範囲外にあることから、このように判定を下すことで、確率 α で判定ミスが生じる危険性がある。そのため、このような判定を下すとき、「危険率 α のもとで帰無仮説を棄却した（危険率 α のもとで標本平均が μ と同値ではないと判断した）」の一文を付け加える必要がある。この危険率 α は有意水準とも呼ばれている。

R による 1 標本 t 検定

次は R を使用して標本 x の平均が 2.0 であるかどうかを判定する例である。まず、T 値を計算し、次に、±t_α/2 の値を計算し、両者を比べて判定を下す。このとき、危険率を 0.05 もとで判定を下すものとする。

x <- c(3.2, 3.6, 2.9, 2.5, 3.1, 2.7, 3.0, 3.2)
n <- length(x)
t.value <- (mean(x) - 2.0) / (sd(x) / sqrt(n))
# 8.602691

err <- qt(0.975, df = n - 1) * sd(x) / sqrt(n)
mean(x) - err
# 2.743258

mean(x) + err
# 3.306742

alpha <- 0.05
t.alpha.2.n <- qt(alpha / 2, df = n - 1)
# -2.364624

t.alpha.2.p <- qt(1 - alpha / 2, df = n - 1)
# 2.364624

p.value <- 2 * pt(- abs(t.value), df = n - 1)
# 5.716248e-05

これにより、T 値（t.value）は、t.value > t.alpha.2.p であるから、危険率 0.05 のもとで帰無仮説を棄却することができる。また、R の t.test 関数を使うと次のように 1 標本 t 検定を行うことができる。

x <- c(3.2, 3.6, 2.9, 2.5, 3.1, 2.7, 3.0, 3.2)
t <- t.test(x, mu = 2.0)
t
# 	One Sample t-test
# 
# data:  x
# t = 8.6027, df = 7, p-value = 5.716e-05
# alternative hypothesis: true mean is not equal to 0
# 95 percent confidence interval:
#  2.743258 3.306742
# sample estimates:
# mean of x
#     3.025

2 標本 t 検定（等分散）

2 標本 t 検定は、2 つのグループの母平均に違いがあるかどうかを検定する方法である。2 つのグループをここで X グループと Y グループとする。また、X グループの母平均を μ_X、Y グループの母平均を μ_Y とおく。このとき、帰無仮説を「X グループの母平均と Y グループの母平均に差がない」とすることができる。

\[ H_{0}: \mu_{X} = \mu_{Y} \]

2 つのグループの母平均に差があるがどうかを検定するために、ここで X グループの標本平均と Y グループの標本平均の差について着目する。母集団 X から標本を抽出したとき、その標本平均 \(\overline{X}\) は \(\mathcal{N} (\mu_{X}, \sigma_{X}^{2}/n_{X}) \) の分布に従う。同様に、母集団 Y から標本を抽出したとき、その標本平均 \(\overline{Y}\) は \(\mathcal{N} (\mu_{Y}, \sigma_{Y}^{2}/n_{Y}) \) の分布に従う。このとき、\(\overline{X}\) と \(\overline{Y}\) が独立であれば、（多変量同時分布の計算を行うことで、）両者の差は次の分布に従う。

\[ \overline{X} - \overline{Y} \sim \mathcal{N}\left( \mu_{X}-\mu_{Y}, \frac{\sigma_{X}^{2}}{n_{X}} + \frac{\sigma_{Y}^{2}}{n_{Y}} \right) \]

これを標準化すると、

\[ Z = \frac{(\overline{X} - \overline{Y}) - (\mu_{X} - \mu_{Y})}{\sqrt{\left( \frac{1}{n_{X}} + \frac{1}{n_{Y}} \right)\sigma^{2}}} \sim \mathcal{N}(0, 1) \]

サンプルサイズが少ないとき、Z は自由度 n_X + n_Y - 2 の t 分布に従う。ここで小サンプルサイズであること示すために、上式中の確率変数 Z を T に置き換えて書くことにする。

\[ Z = T = \frac{(\overline{X} - \overline{Y}) - (\mu_{X} - \mu_{Y})}{\sqrt{\left( \frac{1}{n_{X}} + \frac{1}{n_{Y}} \right)\sigma^{2}}} \sim t(n_{X} + n_{Y} - 2) \]

ここで、母分散 σ² について未知であるから、X グループおよび Y グループの標本から母集団の不偏分散を推定する。

\[ \begin{eqnarray} S^{2}_{pooled} &=& \frac{ \sum_{i}^{n_{X}}(X_{i} - \overline{X})^{2} + \sum_{i}^{n_{X}}(Y_{i} - \overline{Y})^{2} }{(n_{X}-1) + (n_{Y}-1)} \\ &=& \frac{(n_{X}-1)S_{X} + (n_{Y}-1)S_{Y}}{n_{X} + n_{Y} - 2} \end{eqnarray} \]

推定された母集団の不偏分散 S²_pooled を確率変数 T に代入すると次の式を得ることができる。

\[ T = \frac{(\overline{X} - \overline{Y}) - (\mu_{X} - \mu_{Y})}{\sqrt{\left( \frac{1}{n_{X}} + \frac{1}{n_{Y}} \right)S^{2}_{pooled}}} \sim t(n_{X} + n_{Y} - 2) \]

帰無仮説が成り立つとき μ_X = μ_Y である。よって、帰無仮説のもとで T は次のように計算できる。

\[ T = \frac{(\overline{X} - \overline{Y})}{\sqrt{\left( \frac{1}{n_{X}} + \frac{1}{n_{Y}} \right)S^{2}_{pooled}}} \sim t(n_{X} + n_{Y} - 2) \]

このように T 値が求まると、以降、1 標本 t 検定と同様に検定を進めることができる。

R による 2 標本 t 検定（等分散）

R で 2 標本 t 検定を行うとき、t.test 関数に 2 つのグループのデータを与えて実行する。この検定を行うとき、危険率を 0.05 とする。

x <- c(20.5, 5.3, 12.4, 2.9, 12.3, 6.7, 2.1, 13.1)
y <- c(2.4, 16.1, 21.0, 10.9, 20.6, 25.7, 24.2, 18.0)

t <- t.test(x, y, var.equal = TRUE)
t
# 	Two Sample t-test
# 
# data:  x and y
# t = -2.2788, df = 14, p-value = 0.03888
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
#  -15.4324621  -0.4675379
# sample estimates:
# mean of x mean of y
#    9.4125   17.3625

alpha <- 0.05
nx <- length(x)
ny <- length(y)
t.alpha.2.n <- qt(alpha / 2, df = nx + ny - 2)
# -2.144787
t.alpha.2.p <- qt(1 - alpha / 2, df = nx + ny - 2)
# 2.144787

t.test の結果から t 値は -2.2788 であり、これが -t_α/2 = -2.144787 よりも小さいので、危険率 0.05 のもとで帰無仮説を棄却する。よって、X グループと Y グループの母平均が等しくないことが判定された。

2 標本 t 検定（異分散）- Welch の t 検定

2 つのグループの母平均に差が存在するかどうかの検定を行うとき、2 つのグループの分散が異なる場合は、次の式に基づいて T 値を計算する。このとき、T 値は自由度 ν の t 分布に従う。

\[ T = \frac{(\overline{X} - \overline{Y})}{\sqrt{ \frac{S_{X}^{2}}{n_{X}} + \frac{S_{Y}^{2}}{n_{Y}} }} \sim t(\nu) \] \[ \nu = \frac{ \left( \frac{S_{X}^{2}}{n_{X}} + \frac{S_{Y}^{2}}{n_{Y}} \right)^{2} }{\frac{S_{X}^{4}}{n_{X}^{2}(n_{X}-1)} + \frac{S_{Y}^{4}}{n_{Y}^{2}(n_{Y}-1)}} \]

R による 2 標本 t 検定（異分散）

x <- c(20.5, 5.3, 12.4, 2.9, 12.3, 6.7, 2.1, 13.1)
y <- c(1.4, 16.1, 31.0, 10.9, 20.6, 15.7, 24.2, 28.0)

t.test(x, y, var.equal = FALSE)
## 	Welch Two Sample t-test
## 
## data:  x and y
## t = -2.2376, df = 12.026, p-value = 0.04495
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -17.909469  -0.240531
## sample estimates:
## mean of x mean of y
##    9.4125   18.4875

対応のある 2 標本 t 検定

対応のある 2 標本実験では、ほとんどの場合、処理前と処理後に差が生じたかどうかを調べる目的となっている。例えば、マウスの薬剤投与実験において、薬剤投与前と投与後の心拍数に差が生じたかどうかを調べるなどの目的があげられる。

個体	薬剤投与前の心拍数	薬剤投与後の心拍数	差
マウス 1	591	585	-6
マウス 2	615	590	-25
マウス 3	602	583	-19
マウス 4	618	594	-24
マウス 5	596	589	-7

この場合、処理前と処理後の心拍数の差に着目することで、その差が 0 かどうかを検定する 1 標本 t 検定とみなすことができる。

before <- c(591, 615, 602, 618, 596)
after  <- c(585, 590, 583, 594, 589)

t.test(before, after, paired = TRUE)
## 
##         Paired t-test
## 
## data:  before and after
## t = 3.9595, df = 4, p-value = 0.01669
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##   4.840301 27.559699
## sample estimates:
## mean of the differences 
##                    16.2 

diff <- after - before
t.test(diff, rep(0, 5), var.equal = FALSE)
## 	Welch Two Sample t-test
## 
## data:  diff and rep(0, 5)
## t = -3.9595, df = 4, p-value = 0.01669
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -27.559699  -4.840301
## sample estimates:
## mean of x mean of y
##     -16.2       0.0