自己共分散
ある時系列 y1:t に関して、各時点 t における期待値を E[yt] = μt としたとき、時点差 j における yt と yt-j の共分散を、時差 j の自己共分散という。また、j = 0 のときは、yt 自身の分散となる。
\[ Cov(y_{t}, y_{t-j}) = E[(y_{t} - \mu_{t})(y_{t-j} - \mu_{t-j})] \]{yt} が定常過程であるとき、自己共分散を時差 j からなる関数 γ(j) としてみなすことができ、これをとくに自己共分散関数という。
\[ \gamma(j) = Cov(y_{t}, y_{t-j}) = E[(y_{t} - \mu)(y_{t-j} - \mu)] \]自己相関
自己共分散は、上式のように、データの測定単位に依存する。そのため、一般的な時系列解析において、自己共分散を正規化した自己相関が用いられる。時差 j における自己相関は次のように計算される。自己相関は |ρ(j)| ≤ 1 を満たし、その絶対値が 1 に近いほど相関が強い。
\[ \frac{Cov (y_{t}, y_{t-j})}{\sqrt{Var(y_{t})Var(y_{t-j})}}\]y1:t が定常過程であるとき、自己相関は時差 j の関数 ρ(j) とみなすことができ、これをとくに自己相関関数という。
\[ \rho (j) = \frac{Cov (y_{t}, y_{t-j})}{\sqrt{Var(y_{t})Var(y_{t-j})}} = \frac{\gamma(j)}{\gamma(0)} \]自己相関関数における j の値を次々と変化させて、その時の自己相関の変化をグラフに表したものをコレログラムという。
偏自己相関
時点 t と時点 t-1 で自己相関が見られるときに、時点 t と時点 t-2 の自己相関に時点 t-1 の情報が含まれている可能性がある。例えば、ある時系列データに関して、ある日の観測日 yn がその前日の観測値 yn-1 の r 倍となるとき、この時系列データは、
\[ y_{n} = ry_{n-1} \]のようにかける。このとき、その前日の観測値 yn-1 は、それよりも前の日の観測値 yn-2 の r 倍となっているので、上式は
\[ y_{n} = ry_{n-1} = r^{2}y_{n-2} = r'y_{n-2}\]のようにかける。そのため、時点 t と時点 t-1 の自己相関が高ければ、時点 t と時点 t-2 の自己相関も高いと予想される。これは時点 t と時点 t-2 の自己相関の中に時点 t-1 の情報が織り込まれているためである。そこで、時点 t と時点 t-2 の自己相関を計算するときに、時点 t-1 の情報を取り除くことで、時点 t と時点 t-2 の真の自己相関を計算できるようになる。このような相関を偏自己相関という。
時点 t と時点 t-2 の偏自己相関は、「時点 t のうち時点 t-1 で説明できなかった情報 \(y_{t} - \alpha y_{t-1}\)」と「時点 t-2 のうち時点 t-1 で説明できなかった情報 \(y_{t-2} - \beta y_{t-1}\)」の相関である。α は、 \(E[(y_{t} - \alpha y_{t-1})^{2}] \) が最小となるように選ぶ。β に関しても同様に選ぶ。このとき、時点 t と時点 t-2 の偏自己相関を式で表すと次のようになる。
\[ \frac{Cov(y_{t} - \alpha y_{t-1}, y_{t-2} - \beta y_{t-1})}{\sqrt{Var(y_{t} - \alpha y_{t-1})Var(y_{t-2} - \beta y_{t-1})}} \]一般に、時差 j の偏自己相関は、時点 t と時点 t-j の間に存在している j-1 個のデータ yt-(j-1), yt-(j-2), ..., yt-1 の影響を取り除いた後の時点 t と時点 t-j の間の相関である。その偏自己相関は、次の方程式において φh として求まることが知られている。
\[ \begin{pmatrix} 1 & \rho (1) & \cdots & \rho (j-1) \\ \rho (1) & 1 & \cdots & \rho (j-2) \\ \vdots & \vdots & \ddots & \vdots \\ \rho (j-1) & \rho (j-2) & \cdots & 1 \end{pmatrix} \begin{pmatrix} \phi_{1} \\ \phi_{2} \\ \vdots \\ \phi_{h} \end{pmatrix} = \begin{pmatrix} \rho (1) \\ \rho (2) \\ \vdots \\ \rho (h) \end{pmatrix} \]売上高データの自己相関
ある会社の年間売上高データは R の BJsales オブジェクトに保存されている。この売上高データを図示してから、R の acf 関数で自己相関を計算してみる。
data(BJsales)
BJsales
## Time Series:
## Start = 1
## End = 150
## Frequency = 1
## [1] 200.1 199.5 199.4 198.9 199.0 200.2 198.6 200.0 200.3 201.2 201.6 201.5 201.5 203.5 204.9 207.1 210.5 210.5 209.8 208.8 209.5 213.2 213.7 215.1 218.7 219.8 220.5 223.8 222.8 223.8 221.7 222.3
## [33] 220.8 219.4 220.1 220.6 218.9 217.8 217.7 215.0 215.3 215.9 216.7 216.7 217.7 218.7 222.9 224.9 222.2 220.7 220.0 218.7 217.0 215.9 215.8 214.1 212.3 213.9 214.6 213.6 212.1 211.4 213.1 212.9
## [65] 213.3 211.5 212.3 213.0 211.0 210.7 210.1 211.4 210.0 209.7 208.8 208.8 208.8 210.6 211.9 212.8 212.5 214.8 215.3 217.5 218.8 220.7 222.2 226.7 228.4 233.2 235.7 237.1 240.6 243.8 245.3 246.0
## [97] 246.3 247.7 247.6 247.8 249.4 249.0 249.9 250.5 251.5 249.0 247.6 248.8 250.4 250.7 253.0 253.7 255.0 256.2 256.0 257.4 260.4 260.0 261.3 260.4 261.6 260.8 259.8 259.0 258.9 257.4 257.7 257.9
## [129] 257.4 257.3 257.6 258.9 257.8 257.7 257.2 257.5 256.8 257.5 257.0 257.6 257.3 257.5 259.6 261.1 262.9 263.3 262.8 261.8 262.2 262.7
par(mfrow = c(1, 2))
plot(BJsales)
acf(BJsales)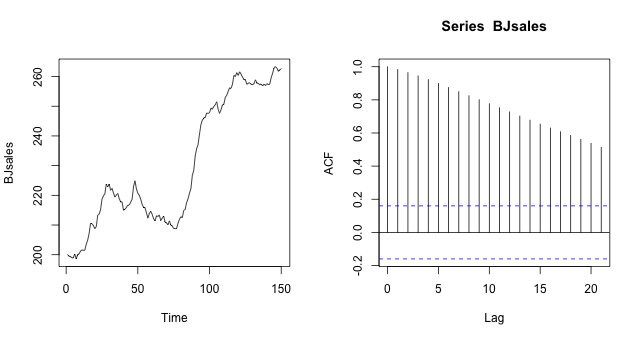
a <- acf(BJsales)
a
## Autocorrelations of series ‘BJsales’, by lag
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
## 1.000 0.983 0.965 0.945 0.923 0.899 0.875 0.850 0.825 0.801 0.777 0.753 0.728 0.702 0.678 0.653 0.630 0.608 0.585 0.561 0.538 0.514ある年 t の値と同年の値は同じであることから、タイムラグ(Lag)がゼロのときの自己相関は 1.00 である。また、ある年 t とその 1 年前の値の自己相関も高く 0.98 であることがわかる。時系列のグラフからもわかるように、ある年 t の値が大きければ、その 1 年後の値も大きい。そのために、連続する 2 年間の自己相関が高いことがわかる。しかし、タイムラグを長くすると、上昇から下落あるいは下落から上昇の区間のデータの影響が加わり、自己相関が徐々に低くなる。
ナイル川の流量データの自己相関
ある場所において観測された 1871-1970 年のナイル川の年間流量データは Nile オブジェクトに保存されている。このナイル川の流量データを図示してから、acf 関数で自己相関を計算してみる。
data(Nile)
Nile
## Time Series:
## Start = 1871
## End = 1970
## Frequency = 1
## [1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 774 840 874 694 940 833 701 916 692 1020 1050
## [40] 969 831 726 456 824 702 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759 781 865 845 944 984 897 822 1010 771 676 649 846 812 742 801 1040 860 874
## [79] 848 890 744 749 838 1050 918 986 797 923 975 815 1020 906 901 1170 912 746 919 718 714 740
par(mfrow = c(1, 2))
plot(Nile)
acf(Nile)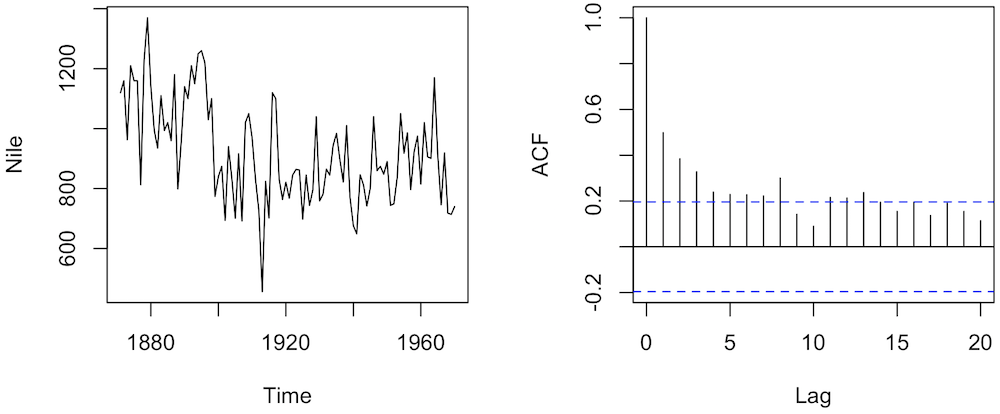
a <- acf(Nile)
a
## Autocorrelations of series ‘Nile’, by lag
## 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## 1.000 0.498 0.385 0.328 0.239 0.228 0.227 0.222 0.300 0.142 0.090 0.215 0.213 0.237 0.195 0.154 0.195 0.136 0.190 0.154 0.114ナイル川の流量データは、前出の売上高データと異なり、右上がりあるいは右下がりの傾向が強くない。言い換えると、ある年の流量は、その前の年の流量にあまり影響されていない。このようなデータはでは、タイムラグが短くても、自己相関が比較的に小さくなる。