時系列解析の基本的な自己回帰モデルや移動平均モデルは、yt を yt-1, yt-2, ... で説明するモデルである。つまり、これらのモデルは、t 時点の観測値を、t よりも前の時点の観測値で説明するモデルである。これらに対して、状態空間モデルは、「状態」と呼ばれる観測されない潜在的な確率変数を導入して、その状態を使用して観測値を説明しようするとモデルである。

状態空間モデルの方程式
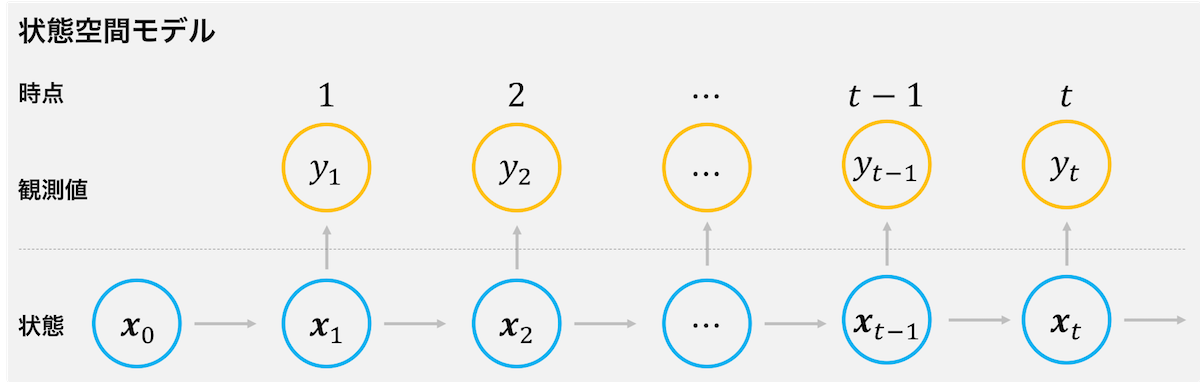
状態空間モデルでは、状態と観測値の 2 つの変数で構成される。t 時点で観測される観測値 yt は状態 xt から生成されると定義する。そして、状態 xt は、状態 xt-1 のみに依存して定まる。これらのことを方程式で表すと次のようになる。
\[ \mathbf{x}_{t} = g(\mathbf{x}_{t-1}, \mathbf{w}_{t}) \] \[ y_{t} = f(\mathbf{x}_{t-1}, v_{t}) \]状態 x に関する方程式を状態方程式、観測値 y に関する方程式を観測方程式という。方程式の中に含まれている関数 g および関数 f は任意の関数である。また、状態方程式中の w を状態雑音といい、何らかの時間的なパターンが潜在していると仮定する。観測方程式中の v を観測雑音といい、これは普通のノイズとして扱い、ノイズが小さいほど、観測値の信頼度が大きい。
これらの方程式に含まれている関数 g、関数 f、雑音 w、 および雑音 v に制約が設けられていない場合の状態空間モデルを一般状態空間モデルとよぶ。また、関数 g および関数 f が線形で、雑音 w および v が正規分布の場合は、とくに線形・正規型(ガウス型)状態空間モデルとよばれている。
状態空間モデルの同時分布
観測値 y1, y2, ..., yT が観測されたときの同時分布は、確率の乗法定理を用いて次のように求めることができる。ただし、ここで状態方程式および観測方程式中のパラメーター(例えば関数 g の係数、vt の分散など)が既知として、パラメーターについて考慮しないこととする。
\[ \begin{eqnarray} p(y_{1:T}, \mathbf{x}_{0:T}) &=& p(y_{T}, y_{1:T-1}, \mathbf{x}_{0:T}) \\ &=& p(y_{T} | y_{1:T-1}, \mathbf{x}_{0:T}) p( y_{1:T-1}, \mathbf{x}_{0:T}) \\ &=& p(y_{T} | y_{1:T-1}, \mathbf{x}_{0:T}) p( y_{1:T-1}, \mathbf{x}_{T}, \mathbf{x}_{0:T-1}) \\ &=& p(y_{T} | y_{1:T-1}, \mathbf{x}_{0:T}) p(\mathbf{x}_{T} |y_{1:T-1}, \mathbf{x}_{0:T-1}) p( y_{1:T-1}, \mathbf{x}_{0:T-1}) \\ &=& \cdots \\ &=& \left( \prod_{t=2}^{T} p(y_{t} | y_{1:t-1}, \mathbf{x}_{0:t}) p(\mathbf{x}_{t} | y_{1:t-1}, \mathbf{x}_{0:t-1}) \right) p(y_{1}, \mathbf{x}_{0:1}) \\ &=& \left( \prod_{t=2}^{T} p(y_{t} | y_{1:t-1}, \mathbf{x}_{0:t}) p(\mathbf{x}_{t} | y_{1:t-1}, \mathbf{x}_{0:t-1}) \right) p(y_{1} | \mathbf{x}_{0:1})p(\mathbf{x}_{1}|\mathbf{x}_{0})p(\mathbf{x}_{0}) \end{eqnarray} \]状態空間モデルにおいて、時点 t における状態は時点 t-1 の状態のみに影響され、観測値に影響されない。よって、状態の確率分布については次式が成り立つ。
\[ p(\mathbf{x}_{t} | \mathbf{x}_{0:t-1}, y_{1:t-1}) = p(\mathbf{x}_{t}|\mathbf{x}_{t-1}) \]また、状態空間モデルにおいて、時点 t の観測地は、時点 t の状態から生成され、他の時点の状態や観測値に影響されない。よって、観測値の確率分布については次式が成り立つ。
\[ p(y_{t}|\mathbf{x}_{0:t}, y_{1:t-1}) = p(y_{t}|\mathbf{x}_{t}) \]このとき、状態の確率分布と観測値の確率分布を用いて、状態空間モデルの同時分布を次のように書き換えることができる。
\[ \begin{eqnarray} p(y_{1:T}, \mathbf{x}_{0:T}) &=& \left( \prod_{t=2}^{T} p(y_{t} | y_{1:t-1}, \mathbf{x}_{0:t}) p(\mathbf{x}_{t} | y_{1:t-1}, \mathbf{x}_{0:t-1}) \right) p(y_{1} | \mathbf{x}_{0:1})p(\mathbf{x}_{1}|\mathbf{x}_{0})p(\mathbf{x}_{0}) \\ &=& \left( \prod_{t=2}^{T} p(y_{t} | \mathbf{x}_{t}) p(\mathbf{x}_{t} | \mathbf{x}_{t-1}) \right) p(y_{1} | \mathbf{x}_{1})p(\mathbf{x}_{1}|\mathbf{x}_{0})p(\mathbf{x}_{0}) \\ &=& \left( \prod_{t=1}^{T} p(y_{t} | \mathbf{x}_{t}) p(\mathbf{x}_{t} | \mathbf{x}_{t-1}) \right) p(\mathbf{x}_{0}) \\ &=& p(\mathbf{x}_{0}) \prod_{t=1}^{T} p(y_{t} | \mathbf{x}_{t}) p(\mathbf{x}_{t} | \mathbf{x}_{t-1}) \end{eqnarray} \]状態空間モデルのパラメーターと尤度
パラメーター θ のもとで観測値 y1, y2, ..., yT が観測されたと考えたとき、状態空間モデルの尤度は次のようにかける。(ここでいうパラメーターとは、方程式の関数 g や h の係数や vt の分散などとする。)
\[ \begin{eqnarray} L(\boldsymbol{\theta};y_{1:T}) &=& p(y_{1:T}; \boldsymbol{\theta}) = p(y_{T}, y_{1:T-1}; \boldsymbol{\theta}) \\ &=& p(y_{T} | y_{1:T-1}; \boldsymbol{\theta}) p(y_{1:T-1}; \boldsymbol{\theta}) \\ &=& \cdots \\ &=& \prod_{t=2}^{T}p(y_{t}|y_{t-1}; \boldsymbol{\theta})p(y_{1};\boldsymbol{\theta}) \end{eqnarray} \]実際にパラメーターを推定するときは、尤度の代わりに対数尤度が用いる。
\[ l(\boldsymbol{\theta};y_{1:T}) = \sum_{t=2}^{T}\log p(y_{t}|y_{t-1}; \boldsymbol{\theta}) \log p(y_{1};\boldsymbol{\theta}) \]パラメーターは、観測値から推定する必要があるが、状態空間モデルにおいて、パラメーターだけでなく、状態も観測値から推定する必要がある。パラメーターに制約を加えれば(例えば線形関係・正規分布を仮定するなど)、パラメーターと状態を効率よく推定できる方法がいくつか知られている。これらの方法には、カルマンフィルタ、拡張カルマンフィルタや粒子フィルタなどがある。逆に、パラメーターに制限を加えることができない場合は、ベイズ推定で、状態とパラメーターの両方を同時にを推定していく必要がある。